- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Совершенные числа
Содержание
- 1. Презентация по математике на тему Совершенные числа
- 2. Натуральные числасумма собственных делителей числа меньше самого
- 3. История совершенных чисел1-е совершенное число:6 = 1
- 4. ЕвклидЧисло видагде p простое и простое является совершенным3-е совершенное число:при р=5 4964-е совершенное число:при р=7 8128
- 5. VIII- XII векааббат Алкуин
- 6. XV век5-е совершенное число:при р = 13 33 550 336
- 7. XVI векКатальди без всяких доказательств утверждал, что
- 8. XVII векМарин МерсеннМерсенн без всяких доказательств заявил,
- 9. XVIII векЛеонард ЭйлерЭйлер доказал, что формула Евклида справедлива для всех чётных совершенных чисел:
- 10. XVIII векЛеонард Эйлер6-е совершенное число:при р =
- 11. 1883 годСельский священник из-под Перми Иван Михеевич
- 12. 1903 годКоул показал, что при р=67 число
- 13. 1911 год10-е совершенное число:при р = 89 54 цифры
- 14. 1914 год11-е совершенное число:при р = 107
- 15. 1932 годЛемер показал, что при р=257 число
- 16. 30 января 1952 годАмериканский математик Робинсон в
- 17. 30 января 1952 годК полуночи 30 января
- 18. июнь 1952 год15-е совершенное число:при р =
- 19. сентябрь 1957 годШведский математик Г. Ризель с
- 20. 1962 год19-е совершенное число:при р = 4253 20-е совершенное число:при р = 4423
- 21. 1965 год21-е совершенное число:при р = 9689
- 22. 2001 годК 2000 году было обнаружено 38
- 23. 15 мая 2004 год41-е совершенное число:при р
- 24. Свойства совершенных чиселВсе совершенные числа являются треугольнымиКаждое
- 25. Проблемы, связанные с совершенными числамиСуществуют ли нечётные совершенные числа?Бесконечна ли последовательность совершенных чисел?
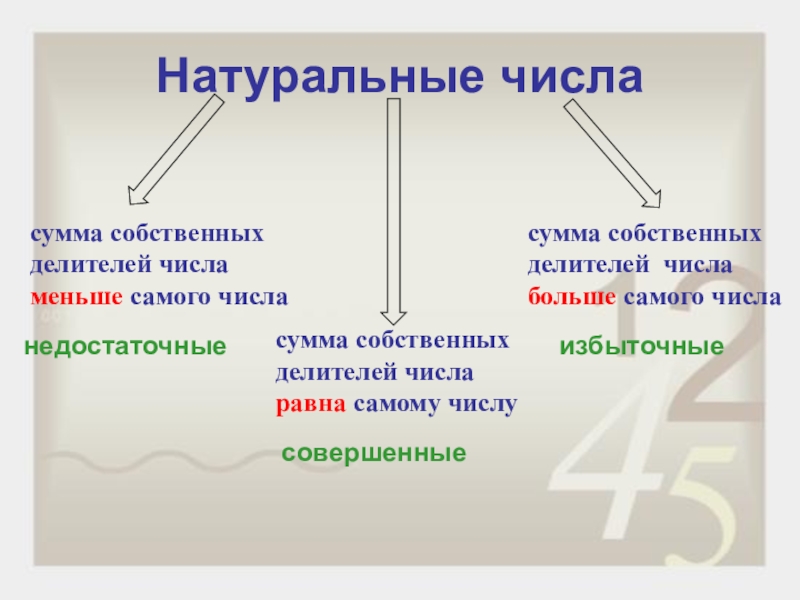
Слайд 2Натуральные числа
сумма собственных делителей числа меньше самого числа
сумма собственных делителей числа
сумма собственных делителей числа больше самого числа
недостаточные
совершенные
избыточные
Слайд 3История совершенных чисел
1-е совершенное число:
6 = 1 + 2 + 3
2-е
28 = 1 + 2 + 4 + 7 + 14
Слайд 4Евклид
Число вида
где p простое и
простое
является совершенным
3-е совершенное число:
при
4-е совершенное число:
при р=7 8128
Слайд 7XVI век
Катальди без всяких доказательств утверждал, что знает шестое и седьмое
шестое: 8 589 869 056 при р=17
седьмое: 137 438 691 328 при р=19
Слайд 8XVII век
Марин Мерсенн
Мерсенн без всяких доказательств заявил, что следующие шесть совершенных
17, 19, 31, 67, 127, 257
Слайд 9XVIII век
Леонард Эйлер
Эйлер доказал, что формула Евклида справедлива для всех чётных
Слайд 10XVIII век
Леонард Эйлер
6-е совершенное число:
при р = 17 8
7-е совершенное число:
при р = 19 137 438 691 328
8-е совершенное число:
при р = 31
2 305 843 008 139 952 128
Слайд 111883 год
Сельский священник из-под Перми Иван Михеевич Первушин нашёл 9-е совершенное
9-е совершенное число:
при р = 61
И сумел вычислить для того времени самое простое число вида
при р=61, равное
2 305 843 009 213 693 951
Слайд 121903 год
Коул показал, что при р=67 число Мерсенна – составное:
А
Слайд 141914 год
11-е совершенное число:
при р = 107 65 цифр
12-е совершенное число:
при р = 127 77 цифр (Э. Люка)
Слайд 151932 год
Лемер показал, что при р=257 число Мерсенна – составное:
А
Слайд 1630 января 1952 год
Американский математик Робинсон в Калифорнийском университете применял ЭВМ
К вечеру 30 января ЭВМ нашла простое число Мерсенна при р=521
13-е совершенное число:
при р = 521 314 цифр
Слайд 1730 января 1952 год
К полуночи 30 января ЭВМ нашла простое число
14-е совершенное число:
при р = 607 366 цифр
Слайд 18июнь 1952 год
15-е совершенное число:
при р = 1279 770
октябрь 1952 год
16-е совершенное число:
при р = 2203 1327 цифр
17-е совершенное число:
при р = 2281 1373 цифр
Слайд 19сентябрь 1957 год
Шведский математик Г. Ризель с помощью ЭВМ нашёл 18-е
18-е совершенное число:
при р = 3217 около 2000 цифр
Слайд 211965 год
21-е совершенное число:
при р = 9689
22-е совершенное число:
при р
23-е совершенное число:
при р = 11213 3376 цифр
Слайд 222001 год
К 2000 году было обнаружено 38 совершенных чисел
В 2001
Слайд 2315 мая 2004 год
41-е совершенное число:
при р = 24 036 583
18 февраля 2005 год
42-е совершенное число:
при р = 25 964 951
Слайд 24Свойства совершенных чисел
Все совершенные числа являются треугольными
Каждое совершенное число можно представить
Сумма величин, обратных всем делителям совершенного числа, равна 2
В двоичной записи совершенного числа сначала идут р единиц, а затем р-1 нулей
Слайд 25Проблемы, связанные с совершенными числами
Существуют ли нечётные совершенные числа?
Бесконечна ли последовательность
