- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Системы линейных уравнений. Подготовлена студентами колледжа к семинарскому занятию
Содержание
- 1. Презентация по математике на тему Системы линейных уравнений. Подготовлена студентами колледжа к семинарскому занятию
- 2. Оценить различные методы решения систем линейных алгебраических
- 3. «Приобретение любого познания всегда полезно для ума,
- 4. МЕТОДЫ РЕШЕНИЯ СИСТЕМ:Метод подстановки(«школьный метод»);Метод сложения уравнений систем («школьный метод»);Метод Крамера;Матричный метод;Метод Гаусса;
- 5. Возможные исходы решения:Система может иметь:единственное решение;бесконечное множество решений;не иметь решений.Например,
- 6. Систему линейных уравнений очень удобно записывать в
- 7. Последовательность решения системы:1. Найти определитель исходной матрицы2.
- 8. ПРЕИМУЩЕСТВА:-удобен для решения систем невысокого порядка;-удобно применять
- 9. НЕДОСТАТКИ МЕТОДА:-если = 0,то матричный
- 10. Метод Крамера Метод Крамера — способ решения квадратных
- 11. Метод КрамераАлгоритм решения: - систему записывают в
- 12. ПРЕИМУЩЕСТВА:- простой метод;- определители вычисляются независимо друг
- 13. НЕДОСТАТКИ: Высокая ресурсоемкость вычислений определителей. С точки
- 14. Дата рождения: 30 апреля 1777 года Место рождения:
- 15. Алгоритм состоит из двух этапов.На первом этапе
- 16. Элементарные преобразования:1. Перемена местами двух любых уравнений2.
- 17. - метод Гаусса прост тем, что для
- 18. Обувная фабрика специализируется по выпуску изделий
- 19. «Как же я раньше не догадывался, что
- 20. Если в математике вы имеете дело с
- 21. Если в задаче по математике вам встретилась
- 22. КластерСистема линейных алгебраических уравнений ГаусаКрамераМетод подстановки Матричный
Слайд 1Системы линейных алгебраических уравнений
Подготовили студенты гр. БУ-23
ГПОУ «Амвросиевский индустриально-
Вощенко Кристина
Склярова Татьяна
Бессарабова Екатерина
Припутень Алина
Припутень Анжелика
Назаренко Сергей
2016 год
Слайд 2Оценить различные методы решения систем линейных алгебраических уравнений с точки зрения
ЦЕЛЬ РАБОТЫ
Слайд 3
«Приобретение любого познания всегда полезно для ума, ибо оно сможет впоследствии
Леонардо да Винчи
Слайд 4МЕТОДЫ РЕШЕНИЯ СИСТЕМ:
Метод подстановки(«школьный метод»);
Метод сложения уравнений систем («школьный метод»);
Метод Крамера;
Матричный
Метод Гаусса;
Слайд 5Возможные исходы решения:
Система может иметь:
единственное решение;
бесконечное множество решений;
не иметь решений.
Например,
Слайд 6Систему линейных уравнений очень удобно записывать в матричном виде
АХ =
А – основная матрица системы,
Х – матрица-столбец неизвестных,
В – матрица-столбец свободных членов
МАТРИЧНЫЙ МЕТОД
Решение системы линейных алгебраических уравнений в матричном виде с невырожденной квадратной матрицей А ищут в виде матричного уравнения,
где
Х = А В
-1
А =
-1
1
detА
A11 A21 A31 ….A n1
A12 A22 A32…. An2
…………………..
An1 An2 An3 …. Ann
Слайд 7Последовательность решения системы:
1. Найти определитель исходной матрицы
2. Найти алгебраические дополнения элементов
3. Составить матрицу из алгебраических дополнений
и транспонировать её
4. Каждый транспонированный элемент матрицы поделить на определитель
МАТРИЧНЫЙ МЕТОД
Слайд 8
ПРЕИМУЩЕСТВА:
-удобен для решения систем невысокого порядка;
-удобно применять тогда, когда нужно решить
-может быть легко реализован на ЭВМ.
МАТРИЧНЫЙ МЕТОД
Слайд 9НЕДОСТАТКИ МЕТОДА:
-если = 0,то матричный метод не применяется;
-в процессе
-если система содержит больше трех уравнений, то нахождение обратной матрицы требует значительных вычислительных усилий.
НЕДОСТАТКИ:
-если определитель системы равен нулю, то матричный метод не применяется;
-в процессе решения матричных уравнений у начинающих могут появиться трудности с умножением матриц;
-если система содержит больше трех уравнений, то нахождение обратной матрицы требует значительных вычислительных усилий
МАТРИЧНЫЙ МЕТОД
Слайд 10 Метод Крамера
Метод Крамера — способ решения квадратных систем линейных алгебраических уравнений
Создан Габриэлем Крамером в 1751 году.
Габриэль Крамер
Дата рождения: 31 июля 1704 года
Место рождения: Женева, Швейцария
Дата смерти: 4 января 1752 года
Место смерти: Баньоль-сюр-Сез, Франция
Научная сфера математика, философия, небесная механика
Слайд 11Метод Крамера
Алгоритм решения:
- систему записывают в матричном виде;
- вычисляют
- вычисляют дополнительные определители системы;
- если главный определитель системы не равен нулю, то находят значения всех неизвестных по формулам:
Слайд 12ПРЕИМУЩЕСТВА:
- простой метод;
- определители вычисляются независимо друг от друга, следовательно, процесс
Метод Крамера
Слайд 13НЕДОСТАТКИ:
Высокая ресурсоемкость вычислений определителей. С точки зрения затрат времени на
если определитель равен нулю, то система имеет бесконечно много решений или несовместна. В этом случае правило Крамера не поможет.
Метод Крамера
Слайд 14Дата рождения: 30 апреля 1777 года
Место рождения: Брауншвейг
Дата смерти: 23 февраля
Научная сфера: математика, физика, астрономия
Альма-матер: Гёттингенский университет
Карл Фридрих Гаусс
немецкий математик, астроном и физик
Метод Гаусса
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных
Иоганн Карл Фридрих Гаусс еще при жизни получил звание величайшего математика всех времен, гения и даже прозвище «короля математики». Портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок
Слайд 15Алгоритм состоит из двух этапов.
На первом этапе осуществляется прямой ход, когда
На втором этапе осуществляется обратный ход, суть которого заключается в том, чтобы последовательно найти все неизвестные из треугольной системы
Метод Гаусса
Слайд 16Элементарные преобразования:
1. Перемена местами двух любых уравнений
2. Умножение обеих частей любого
3. Прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число
Элементарные преобразования удобно проводить не с уравнениями, а с расширенной матрицей системы
Метод Гаусса
Слайд 17- метод Гаусса прост тем, что для его освоения достаточно знаний
-метод Гаусса - наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений.
Правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу!
Метод Гаусса
ПРЕИМУЩЕСТВА:
Слайд 18
Обувная фабрика специализируется по выпуску изделий трёх видов: сапог, кроссовок и
Найти ежедневный объём выпуска каждого вида обуви.
Решение: Пусть ежедневно фабрика выпускает х пар сапог, у пар кроссовок и z пар ботинок. Тогда в соответствии с расходом сырья каждого вида имеем систему
5x+3e+4z=2700
2x+y+z=900
3x+2y+2z=1600
Решая систему любым способом, находим:(200,300,200), т.е. фабрика выпускает ежедневно 200 сапог, 300 кроссовок и 200 ботинок.
Слайд 20Если в математике вы имеете дело с дробными числами, то все
Скверным признаком, который свидетельствует об ошибке в вычислениях (реже-об опечатке), является «плохая» нижняя строка в методе Гаусса.
Любое задание следует стремиться выполнить самым рациональным способом. Хотя бы потому, что это экономит время и нервы, а также снижает вероятность допустить ошибку.
После того, как решена ЛЮБАЯ система уравнений ЛЮБЫМ способом , настоятельно рекомендуется выполнить проверку (устно, на черновик либо на калькуляторе).Благо, делается это легко и быстро!
Слайд 21Если в задаче по математике вам встретилась система двух линейных уравнений
Рекомендуем вам скачать программу автоматизированного решения систем по формулам Крамера и с помощью обратной матрицы. Всегда приятно знать правильные ответы заранее, более того, программа позволит сразу обнаружить ошибку по ходу решения задачи, что значительно сэкономит время!
Наиболее универсальным способом решения системы является метод исключения неизвестных (метод Гаусса)
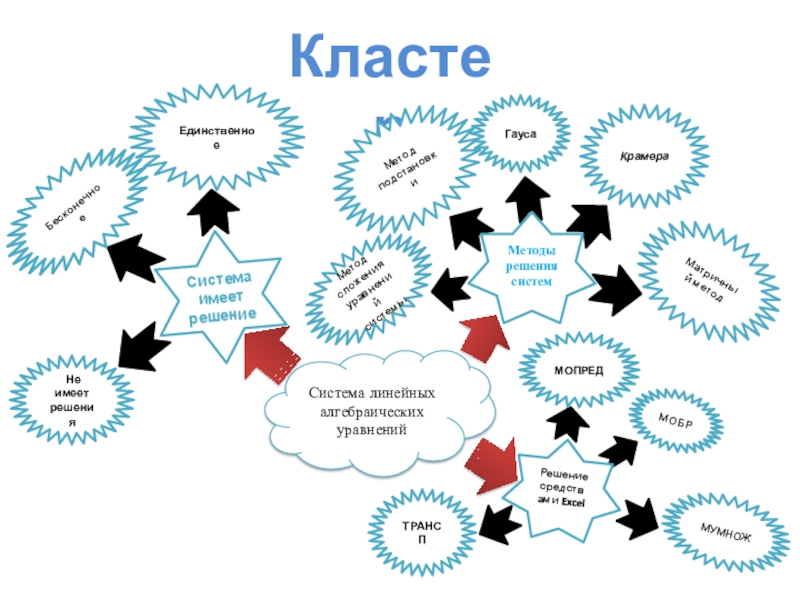
Слайд 22Кластер
Система линейных алгебраических уравнений
Гауса
Крамера
Метод подстановки
Матричный метод
Методы решения систем
Метод сложения
Бесконечное
Единственное
Не имеет решения
Система имеет решение
Решение средствами Excel
МОБР
ТРАНСП
МОПРЕД
МУМНОЖ
Бесконечное