«…Творчество, конечно, состоит не в том, чтобы составлять бесконечные комбинации, а в том, чтобы создавать полезные, а таких не особенно много. Творить – это значит различать, выбирать».
А. Пуанкаре
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Решение комбинаторных задач
Содержание
- 1. Презентация по математике на тему Решение комбинаторных задач
- 2. Цели:Образовательные: познакомить с разделом математики: "Комбинаторика", с
- 3. Что
- 4. Решение комбинаторных задач Основные способы решения комбинаторных
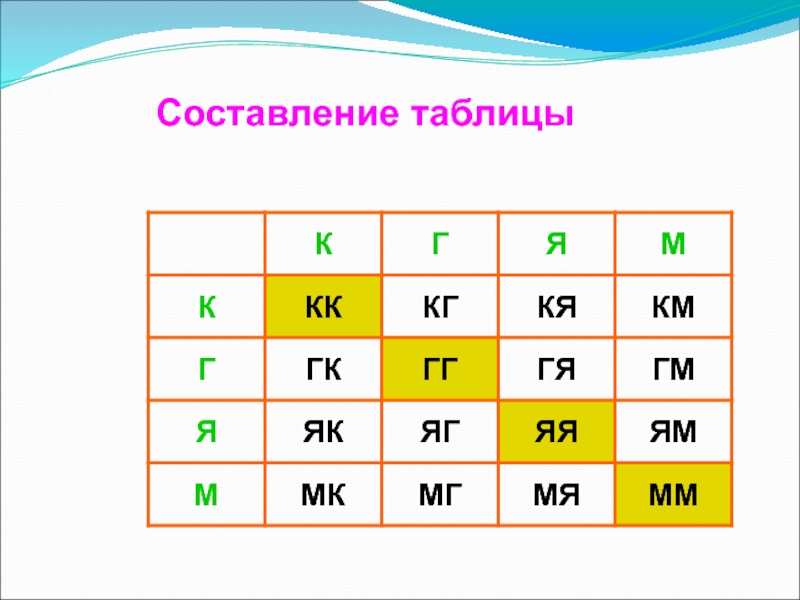
- 5. Задача (составление таблицы)Для начинки пирога бабушка решила
- 6. Составление таблицы
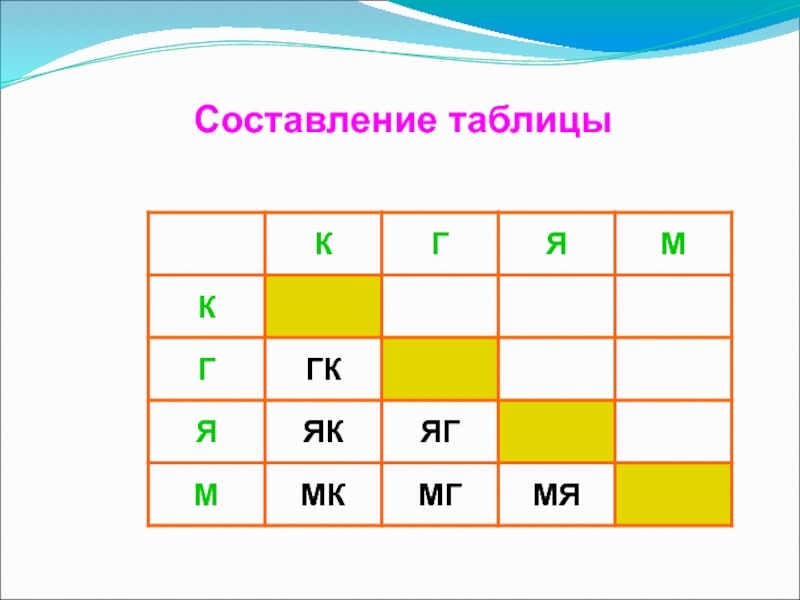
- 7. Составление таблицы
- 8. Перечислите все возможные варианты обедов из трех
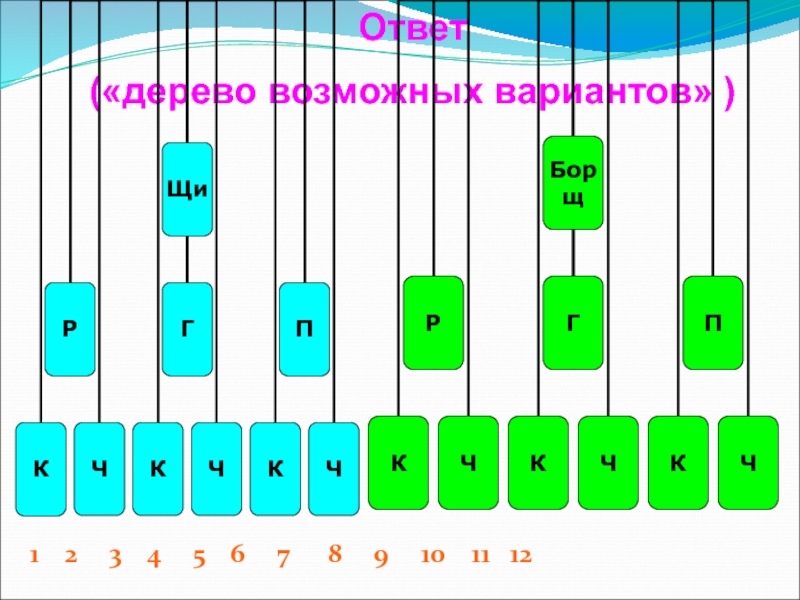
- 9. Ответ(«дерево возможных вариантов» )1 2
- 10. Задача« 5 финалистов конкурса «Учитель года- 2014»,
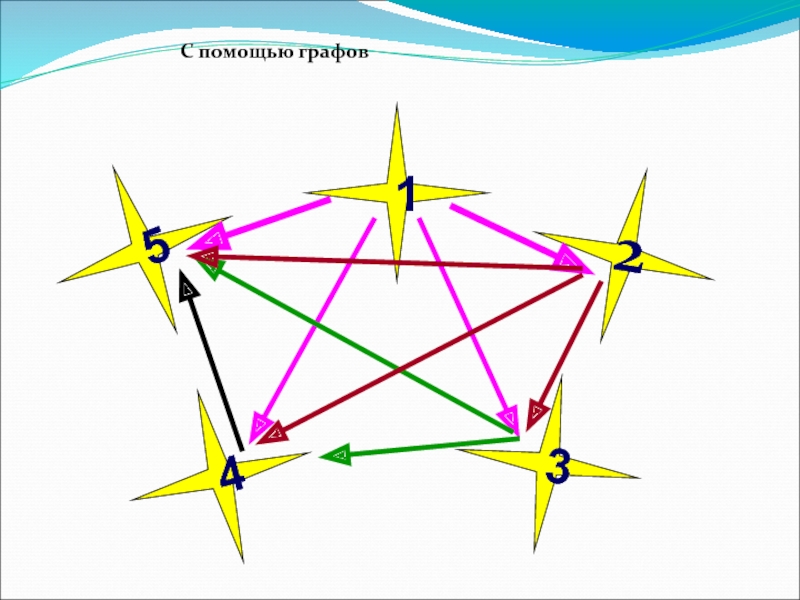
- 11. 35142С помощью графов
- 12. Слайд 12
- 13. «День – ночь»6 вариантовКатяМишаЛизаМишаКатяЛизаЛизаМишаКатяКатяЛизаМишаМишаЛизаКатяЛизаМишаКатя
- 14. Два основных правилаПравило суммы Если некоторый объект
- 15. ЗадачаВ магазине «Все для чая» есть 6
- 16. ЗадачаНа полке стояли 7 книг российских
- 17. Слайд 17
- 18. РазмещенияРазмещения – соединения, содержащие по m предметов
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Задача 3.Сколько существует семизначных телефонных номеров, в
- 25. Слайд 25
- 26. Задача 5. В классе 16 мальчиков и
- 27. РефлексияСегодня я узнал…Было интересно…Было трудно…Я выполнял задания…Я
- 28. Спасибо за внимание!
Слайд 1 Мастер-класс по математике по теме «Решение комбинаторных задач» Мигунова О.В.,
Слайд 2Цели:
Образовательные:
познакомить с разделом математики: "Комбинаторика", с его историей, основными понятиями
способствовать созданию учебного проекта как показатель качественного изучения темы занятия.
Развивающие:
развивать аналитические способности, логическое мышление,
индивидуальные способности, создавая комфортную психологическую обстановку для каждого.
Воспитывающие:
формировать активность личности, умение работать в группе.
Слайд 3
Что такое комбинаторика?
КОМБИНАТОРИКА (от латинского слова «combina» – «сочетать», «соединять»)–
Слайд 4Решение комбинаторных задач
Основные способы решения комбинаторных задач:
ГРАФ – совокупность объектов со
ДЕРЕВО ВОЗМОЖНЫХ ВАРИАНТОВ – граф, схема, отражающая структуру задачи, упорядочения многошагового процесса принятия решений. Ветви дерева отображают различные события, которые могут иметь место, а корень дерева – состояние, в котором возникает необходимость выбора.
ОРГАНИЗОВАННЫЙ ПЕРЕБОР – строгий порядок разбора всех случаев, возможных решений.
ТАБЛИЦА – это перечень сведений, числовых данных, приведенных в определенную систему и разнесенных по графам (строкам и столбцам).
Слайд 5Задача
(составление таблицы)
Для начинки пирога бабушка решила смешать два продукта. Сколько
Слайд 8Перечислите все возможные варианты обедов из трех блюд (одного первого, одного
два первых блюда: щи (Щ), борщ (Б);
три вторых блюда: рыба (Р), гуляш (Г), плов (П);
два третьих блюда: компот (К), чай (Ч).
Задача
(«дерево возможных вариантов» )
Слайд 10Задача
« 5 финалистов конкурса «Учитель года- 2014», решили обменяться впечатлениями о
Слайд 12
Участвуют три игрока. Они садятся на стулья. По команде ведущего «День!» ребята встают и могут передвигаться. По команде ведущего «Ночь!» они садятся на стулья, но так, чтобы каждый раз порядок расположения их был другой. Все остальные следят за тем, чтобы играющие выполняли поставленное условие. Игра продолжается до тех пор, пока не обнаружатся все возможные варианты.
Вопрос: сколько всего вариантов получится?
Решение:
Слайд 13«День – ночь»
6 вариантов
Катя
Миша
Лиза
Миша
Катя
Лиза
Лиза
Миша
Катя
Катя
Лиза
Миша
Миша
Лиза
Катя
Лиза
Миша
Катя
Слайд 14Два основных правила
Правило суммы
Если некоторый объект А можно выбрать m
Правило произведения
Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары А и В можно осуществить m · n способами.
Слайд 15Задача
В магазине «Все для чая» есть 6 разных чашек и 4
Решение.
Чашку мы можем выбрать 6-ю способами, а блюдце 4-я способами. Так как нам надо купить пару чашку и блюдце, то это можно сделать 6 · 4 = 24 способами (по правилу произведения).
Ответ: 24.
Слайд 16
Задача
На полке стояли 7 книг российских авторов и 4 книги
Решение: каждую книгу российского автора мы можем выбрать 7-ю способами, а кждую книгу зарубежного автора- 4-мя способами. Поскольку нужно выбрать одну книгу любого автора, то
7+4=11 способов
Ответ: 11 способов
Слайд 17
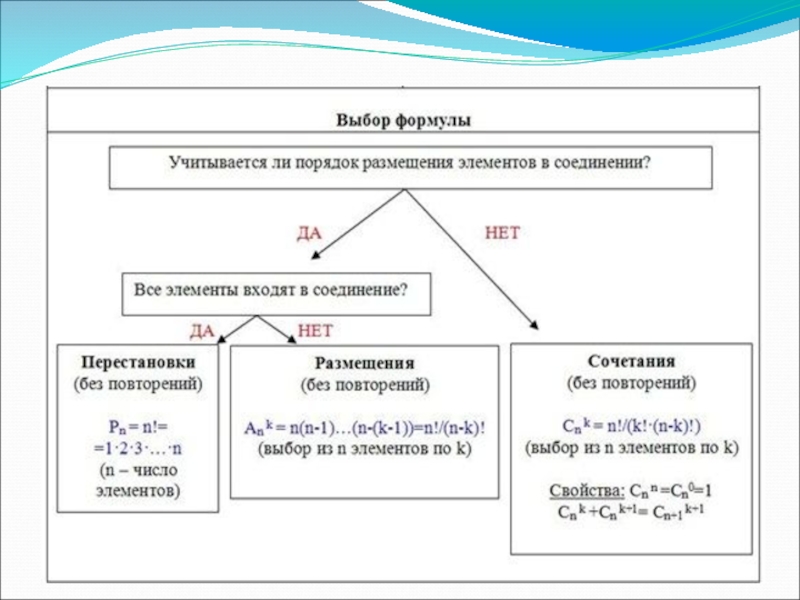
Слайд 18Размещения
Размещения – соединения, содержащие по m предметов из числа n данных,
В комбинаторике размещением называется расположение “предметов” на некоторых “местах” при условии, что каждое место занято в точности одним предметом и все предметы различны.
В отличие от сочетаний размещения учитывают порядок следования предметов. Так, например, наборы < 2,1,3 > и < 3,2,1 > являются различными, хотя состоят из одних и тех же элементов {1,2,3} (то есть, совпадают как сочетания).
Слайд 19
Слайд 20
Сочетания-соединения, содержащие по m предметов из n, различающиеся друг от друга, по крайней мере, одним предметом; число их .
Таким образом, количество вариантов при сочетании будет меньше количества размещений.
В комбинаторике сочетанием из n по m называется набор m элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Слайд 21
Слайд 23
Найдите количество трехзначных чисел, которые можно составить
из цифр 1, 2, 3, 4, 5, 6, 7, если цифры в числе повторяться не могут.
Решение.
Для выбора формулы выясняем, что для чисел, которые мы будем составлять, порядок учитывается и не все элементы одновременно выбираются. Значит, это соединение – размещение из 7 элементов по 3. Воспользуемся формулой для числа размещений:
3
A7 = 7(7 – 1)(7 – 2) = 7 · 6 · 5 = 210 чисел.
Ответ: 210.
Слайд 24Задача 3.
Сколько существует семизначных телефонных номеров, в которых все цифры разные,
Решение.
На первый взгляд эта задача такая же, как и предыдущая, но сложность в том, что надо не учитывать те соединения, которые начинаются с нуля. Значит необходимо из существующих 10-ти цифр составить все семизначные номера телефонов, а потом от полученного числа отнять количество номеров, начинающихся с нуля. Формула будет иметь вид:
7 6
A10 – A9 = 10 · 9 · 8 · 7 · 6 · 5 · 4 – 9 · 8 · 7 · 6 · 5 · 4 = 544 320.
Ответ: 544 320.
Слайд 25
Слайд 26Задача 5.
В классе 16 мальчиков и 12 девочек. Для уборки
Решение.
Сначала отдельно выберем 4 мальчика из 16 и 3 девочки из 12. Так как порядок размещения не учитывается, то соответственные соединения – сочетания без повторений. Учитывая необходимость одновременного выбора и мальчиков, и девочек, используем правило произведения. В результате число способов будет вычисляться таким образом:
4 3
С16 · С12 = (16!/(4! · 12!)) · (12!/(3! · 9!)) = ((13 · 14 · 15 · 16) / (2 · 3 · 4)) ·((10 · 11 · 12) / (2 · 3)) = 400 400.
Ответ: 400 400.
Слайд 27Рефлексия
Сегодня я узнал…
Было интересно…
Было трудно…
Я выполнял задания…
Я понял, что…
Теперь я могу…
Я
Я приобрёл…
Я научился…
У меня получилось…
Я смог…
Я попробую…
Меня удивило…
Урок дал мне для жизни…
Мне захотелось…