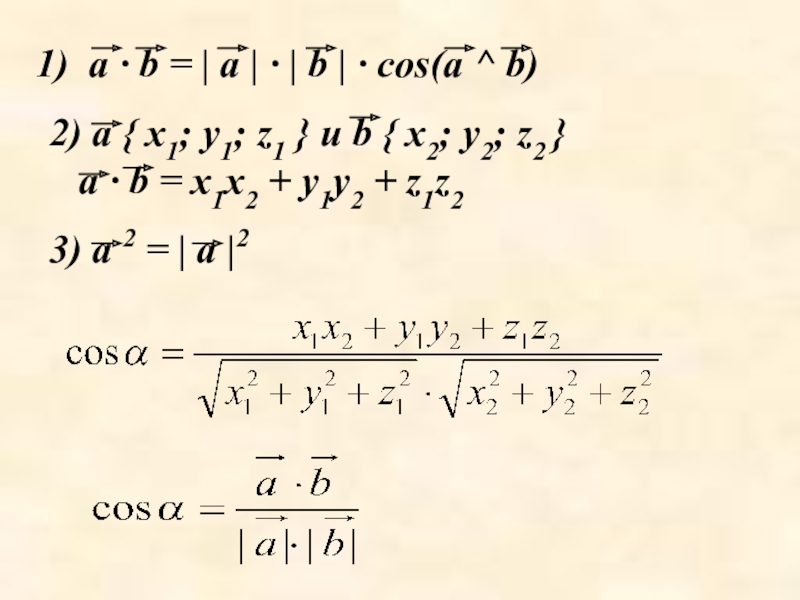- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Прямоугольная система координат в пространстве
Содержание
- 1. Презентация по математике на тему Прямоугольная система координат в пространстве
- 2. Вы уже знакомы с прямоугольной (Декартовой) системой
- 3. А, вот, прямоугольную систему координат в пространстве ввёл швейцарский, немецкий, российский математик Леонард Эйлер в XVIIIв.
- 4. Прямые с выбранными на них
- 5. Три плоскости, проходящие через
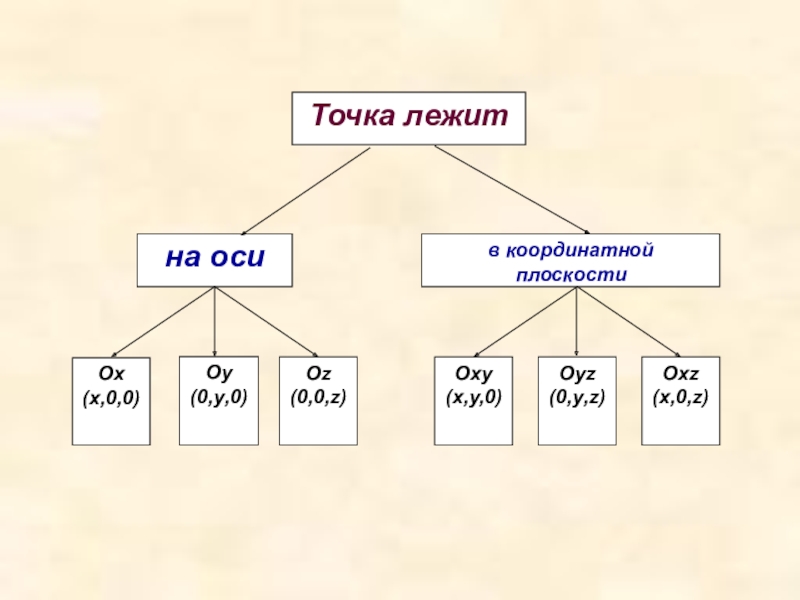
- 6. В прямоугольной системе координат каждой
- 7. Нахождение точки на координатной плоскости.Если, например, точка
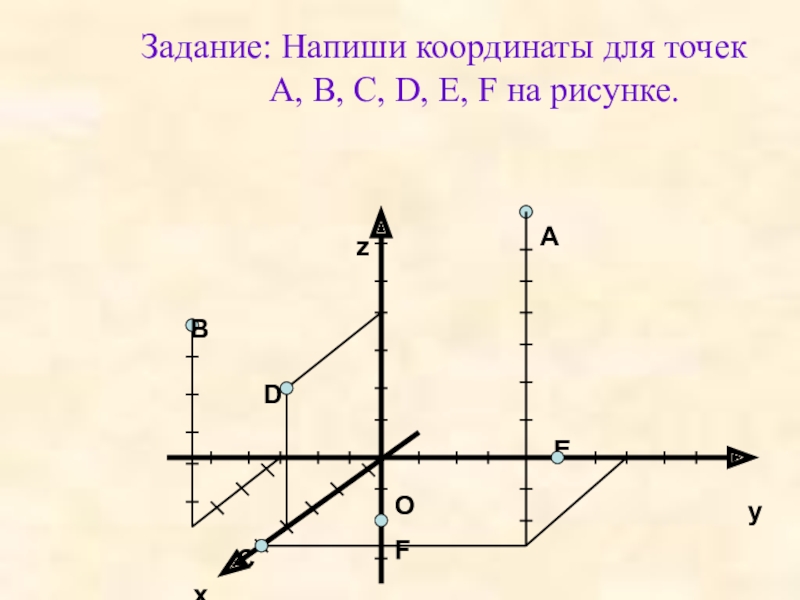
- 8. Задание: Напиши координаты для точек A, B, C, D, E, F на рисунке.BCOEFDzyxA
- 9. Ответы.A(5; 4; 10),B(4; -3; 6),C(5; 0; 0),D(4; 0; 4),E(0; 5; 0),F(0; 0; -2).Сравни свои ответы.
- 10. Оу(0,у,0)
- 11. Если М ОХУ, то
- 12. Координаты вектора в пространстве
- 13. Единичный вектор – вектор, длина которого равна
- 14. Любой вектор ā можно разложить по координатным
- 15. Запись координат вектора.Координаты вектора а будут записываться
- 16. Сложение векторовПравило треугольника.Правило параллелограмма.Правило многоугольника.Правило параллелепипеда.
- 17. Правило треугольникаАBC
- 18. Правило треугольникаАBCДля любых трех точек А, В и С справедливо равенство:
- 19. Правило параллелограммаАBC
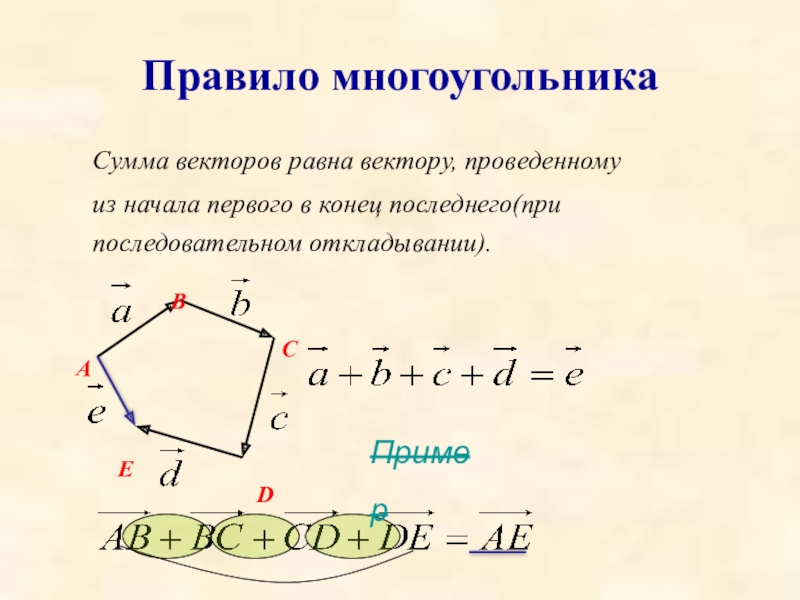
- 20. Правило многоугольникаСумма векторов равна вектору, проведенномуиз начала первого в конец последнего(при последовательном откладывании).BACDEПример
- 21. Правило параллелепипедаBАCDA1B1C1D1Вектор, лежащий на диагонали параллелепипеда, равен
- 22. Угол между векторами
- 23. Угол между двумя ненулевыми векторами называется угол между направлениями этих векторов.)abab
- 24. ОАВα Если а || b и а
- 25. Слайд 25
- 26. Скалярное произведение векторов
- 27. Скалярное произведениеСкалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
- 28. a · b = | a
- 29. Спасибо за внимание!
Слайд 2Вы уже знакомы с прямоугольной (Декартовой) системой координат на плоскости, которую
в XIX в. ввёл
французский
математик
Рене Декарт
Слайд 3А, вот, прямоугольную систему координат в пространстве ввёл швейцарский,
немецкий,
российский
математик
Леонард Эйлер
в XVIIIв.
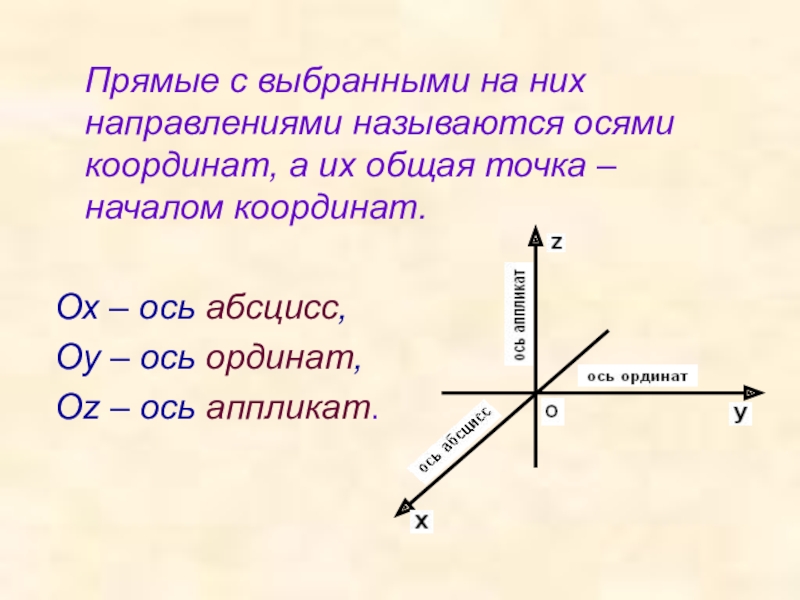
Слайд 4 Прямые с выбранными на них направлениями называются осями координат,
Ох – ось абсцисс,
Оу – ось ординат,
Оz – ось аппликат.
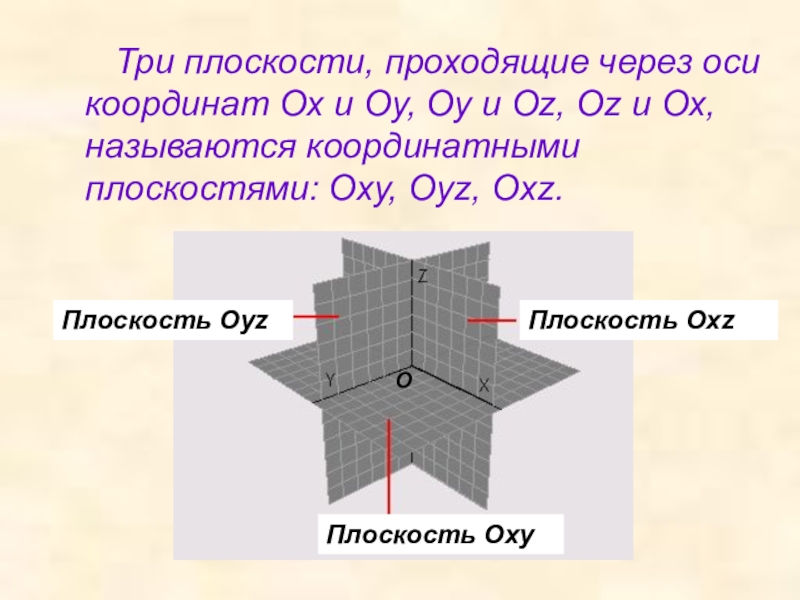
Слайд 5 Три плоскости, проходящие через оси координат Ох и
Плоскость Oxz
Плоскость Oxy
Плоскость Oyz
O
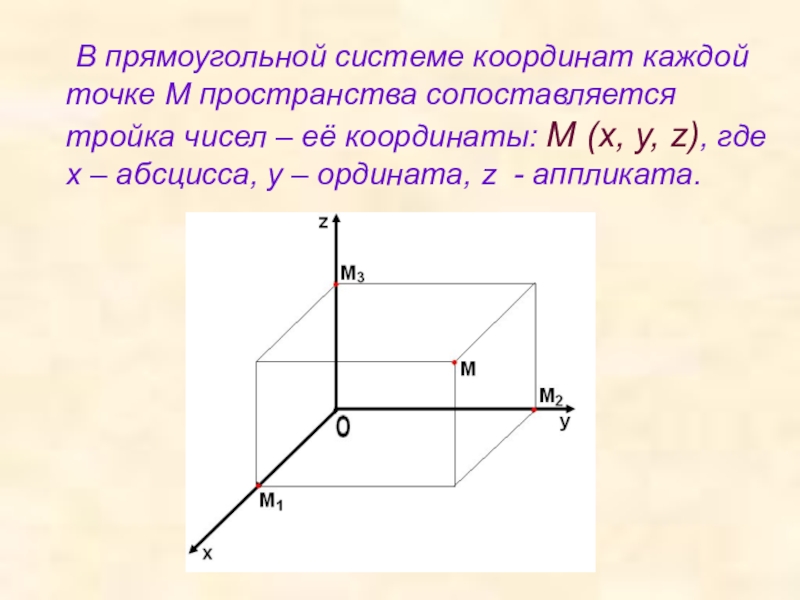
Слайд 6 В прямоугольной системе координат каждой точке М пространства сопоставляется
Слайд 7Нахождение точки на координатной плоскости.
Если, например, точка M лежит на координатной
Слайд 9Ответы.
A(5; 4; 10),
B(4; -3; 6),
C(5; 0; 0),
D(4; 0; 4),
E(0; 5; 0),
F(0;
Сравни свои ответы.
Слайд 11Если М ОХУ, то z=0
Если М
Если М OУZ, то X=0
Если М ОХ, то У=0 и Z=0
Если М OУ, то Х=0 и Z=0
Если М OZ, то Х=0 и У=0
Нахождение точки на координатной плоскости.
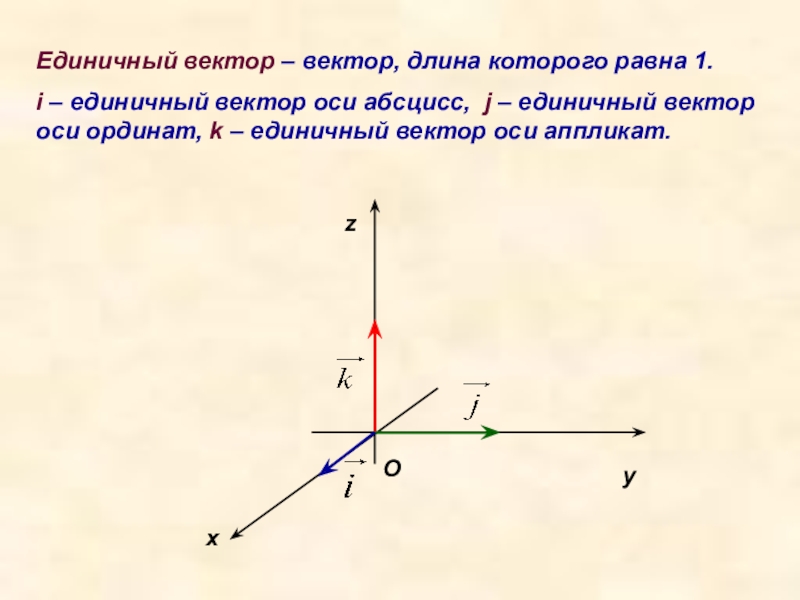
Слайд 13Единичный вектор – вектор, длина которого равна 1.
i – единичный вектор
x
z
y
O
Слайд 14Любой вектор ā можно разложить по координатным векторам, т.е. представить в
Нулевой вектор можно представить в виде:
Координаты равных векторов соответственно равны, т.е., если
ā { x1; y1; z1 } = b { x2; y2; z2 }, то
x1 = x2, y1 = y2, z1 = z2.
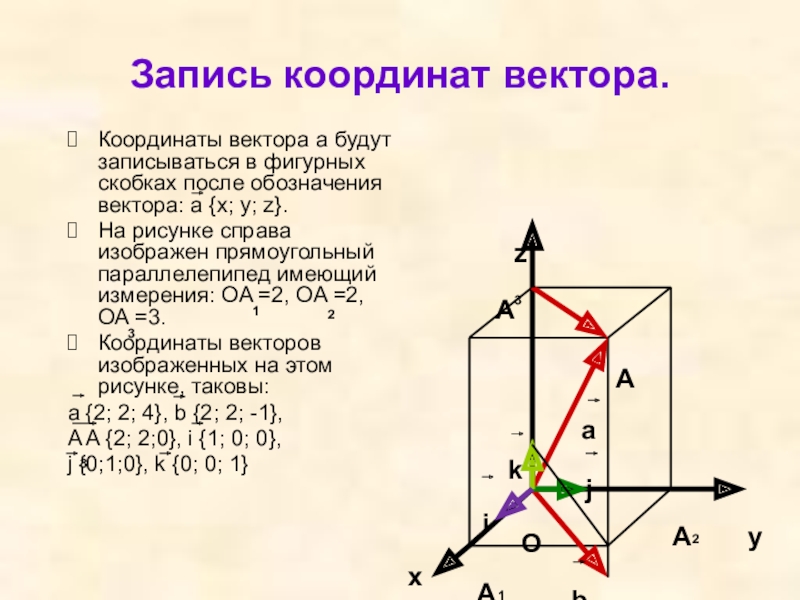
Слайд 15Запись координат вектора.
Координаты вектора а будут записываться в фигурных скобках после
На рисунке справа изображен прямоугольный параллелепипед имеющий измерения: OA =2, OA =2, OA =3.
Координаты векторов изображенных на этом рисунке, таковы:
a {2; 2; 4}, b {2; 2; -1},
A A {2; 2;0}, i {1; 0; 0},
j {0;1;0}, k {0; 0; 1}
A
A
A
A
O
y
x
z
a
j
i
k
b
3
2
1
1
2
3
3
Слайд 16Сложение векторов
Правило треугольника.
Правило параллелограмма.
Правило многоугольника.
Правило параллелепипеда.
Слайд 20Правило многоугольника
Сумма векторов равна вектору, проведенному
из начала первого в конец последнего(при
B
A
C
D
E
Пример
Слайд 21
Правило параллелепипеда
B
А
C
D
A1
B1
C1
D1
Вектор, лежащий на диагонали параллелепипеда, равен сумме векторов, проведенных из
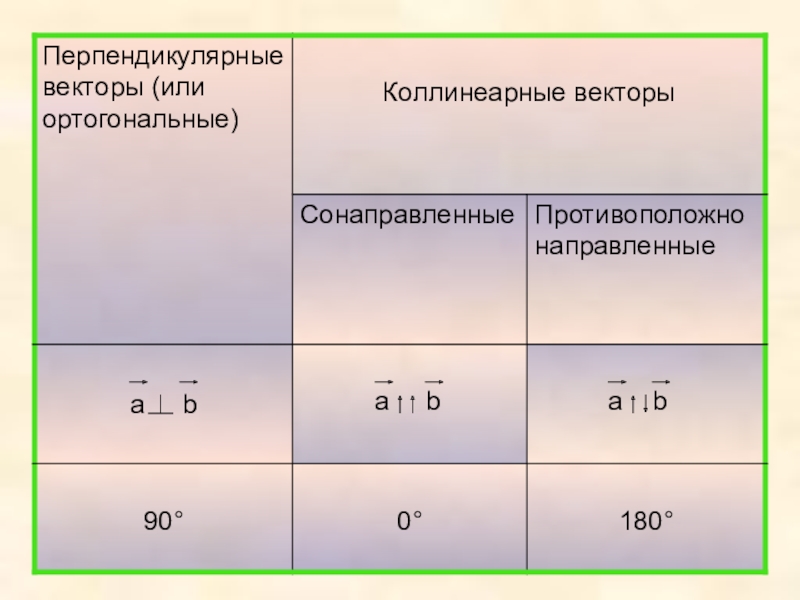
Слайд 23Угол между двумя ненулевыми векторами называется угол между направлениями этих векторов.
)
a
b
a
b
Слайд 24О
А
В
α
Если а || b и а и b сонаправлены, то
Если a || b и a и b противоположно направлены, то α = 180°.
Если а ⊥ b, то α = 90°.
Слайд 27Скалярное произведение
Скалярным произведением двух векторов называется произведение их длин на косинус
Слайд 28 a · b = | a | · | b
2) a { x1; y1; z1 } и b { x2; y2; z2 } a · b = x1x2 + y1y2 + z1z2
3) a 2 = | a |2