- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему производная и ее применение
Содержание
- 1. Презентация по математике на тему производная и ее применение
- 2. Происхождение производной.В конце 17 века в Европе
- 3. Исаак Ньютон (1643 – 1727)Готфрид Вильгельм Лейбниц (1646 – 1716)
- 4. Происхождение производной.Ряд задач дифференциального исчисления был решен
- 5. Памятник Ньютону в Кэмбридже.
- 6. Ньютон пришел к понятию производной, исходя из
- 7. В подходе Лейбница к математическому анализу
- 8. Памятник Лейбницу в Лейпциге.
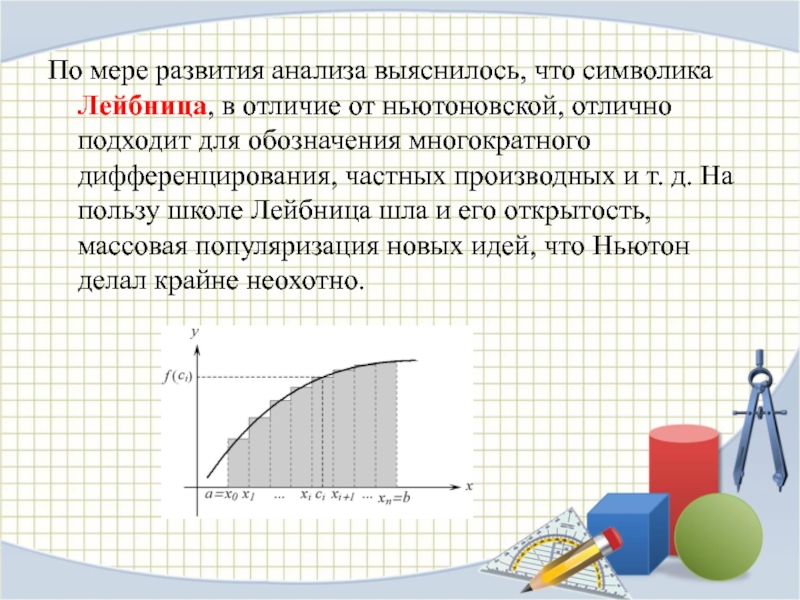
- 9. По мере развития анализа выяснилось, что символика
- 10. Работы Лейбница по математике многочисленны и разнообразны.В
- 11. В1672 году Лейбниц изобретает собственную конструкцию арифмометра,
- 12. Производной функции у = f(x), заданной на
- 13. Нахождение производной называют дифференцированием
- 14. Таблица производных
- 15. Правила нахождения производной1. Если функции u(x) и
- 16. Правила нахождения производной3. Если функции u(x) и
- 17. Правила нахождения производной5. Если функции u(x) и
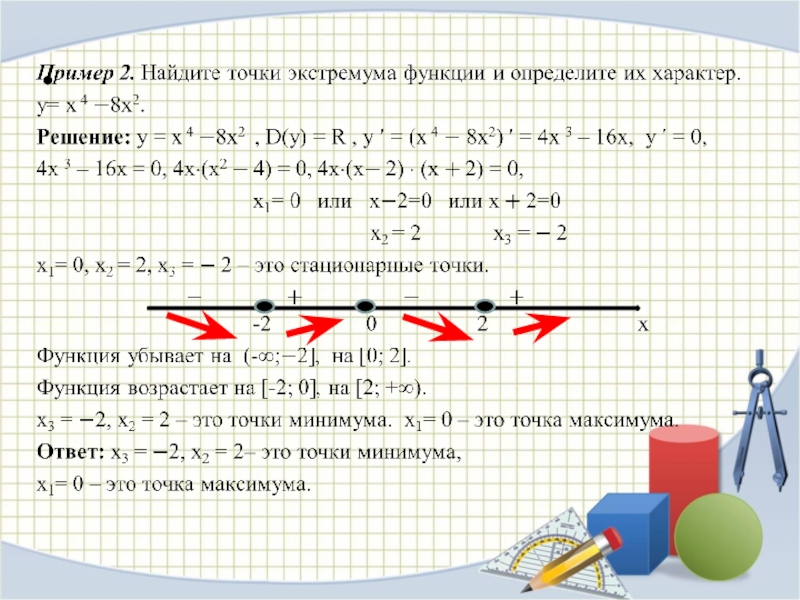
- 18. Примеры
- 19. Примеры
- 20. подсказкаТело, подброшенное вверх движется по закону s(t)
- 21. ЗАДАЧА №2 При
- 22. “При изучении наук примеры не менее поучительны, нежели правила” “Примеры учат больше, чем теория”.И. НьютонМ. Ломоносов
- 23. Примеры
- 24. Слайд 24
- 25. Производнаяи ее применение
- 26. Правильный ответПравильный ответПравильный ответПравильный ответПравильный ответНайдите производные функций:
- 27. Найдите производную функции(устно):а) у = 6х5 –
- 28. Найдите производную функции(устно): Правильный ответПравильный ответПравильный ответПравильный ответ
- 29. Слайд 29
- 30. 3.4.5.
- 31. k = f ′(xo) = tg α
- 32. Общий вид уравнения касательнойy = f ′(xo)(x
- 33. Одна из основных задач исследования функции –
- 34. Алгоритм решения неравенств методом интервалов:Выделить функцию y=f(x).Найти
- 35. Решите неравенство:1.
- 36. Алгоритм нахождения промежутков возрастания (убывания) функции y=f(x):Найти
- 37. Найдите промежутки возрастания и убывания функции:1. 2. f´(x)=0, если 3.Ответ:
- 38. f′(x)xoМинимум функцииТочка хо называется точкой минимума функции
- 39. xoМаксимум функцииТочка хо называется точкой максимума функции
- 40. Алгоритм исследованияфункции на монотонность1о Дифференцируем функцию:
- 41. Алгоритм исследованияфункции на экстремумы1о Дифференцируем функцию:
- 42. Примеры
- 43. Слайд 43
- 44. +++––
- 45. Спасибо за внимание!
Происхождение производной.В конце 17 века в Европе образовались две крупные математические школы. Главой одной из них был Готфрид Вильгельм фон Лейбниц. Его ученики и сотрудники – Лопиталь, братья Бернулли, Эйлер жили и творили на континенте. Вторая
Слайд 2Происхождение производной.
В конце 17 века в Европе образовались две крупные математические
школы. Главой одной из них был Готфрид Вильгельм фон Лейбниц. Его ученики и сотрудники – Лопиталь, братья Бернулли, Эйлер жили и творили на континенте. Вторая школа, возглавляемая Исааком Ньютоном, состояла из английских и шотландских ученых. Обе школы создали новые мощные алгоритмы, приведшие по сути к одним и тем же результатам –
к созданию дифференциального и
интегрального исчисления.
Слайд 4Происхождение производной.
Ряд задач дифференциального исчисления был решен еще в древности. Такие
задачи можно найти у Евклида и у Архимеда, однако основное понятие – понятие производной функции – возникло только в17 веке в связи с необходимостью решить ряд задач из физики, механики и математики, в первую очередь следующих двух: определение скорости прямолинейного неравномерного движения и построения касательной к произвольной плоской кривой.
Первую задачу: о связи скорости и пути прямолинейно и неравномерно движущейся точки впервые решил Ньютон. Он пришел к формуле :
Первую задачу: о связи скорости и пути прямолинейно и неравномерно движущейся точки впервые решил Ньютон. Он пришел к формуле :
Слайд 6Ньютон пришел к понятию производной, исходя из вопросов механики. Свои результаты
в этой области он изложил в трактате «Метод флюксий и бесконечных рядов». Написана работа была в 60-е годы 17 века, однако опубликована после смерти Ньютона. Ньютон не заботился о том, чтобы своевременно знакомить математическую общественность со своими работами.
Флюксией называлась производная функции – флюэнты.
Флюэнтой таже в дальнейшем называлась первообразная функция.
Флюксией называлась производная функции – флюэнты.
Флюэнтой таже в дальнейшем называлась первообразная функция.
Слайд 7В подходе Лейбница к математическому анализу были некоторые особенности. Лейбниц мыслил
высший анализ не кинематически, как Ньютон,
а алгебраически. Он шел к своему открытию от анализа бесконечно малых величин и теории бесконечных рядов.
В 1675 году Лейбниц завершает свой вариант математического анализа, тщательно продумывает его символику и терминологию, отражающую существо дела. Почти все его нововведения укоренились в науке и только термин «интеграл» ввёл Якоб Бернулли (1690), сам Лейбниц вначале называл его просто суммой.
В 1675 году Лейбниц завершает свой вариант математического анализа, тщательно продумывает его символику и терминологию, отражающую существо дела. Почти все его нововведения укоренились в науке и только термин «интеграл» ввёл Якоб Бернулли (1690), сам Лейбниц вначале называл его просто суммой.
Слайд 9По мере развития анализа выяснилось, что символика Лейбница, в отличие от
ньютоновской, отлично подходит для обозначения многократного дифференцирования, частных производных и т. д. На пользу школе Лейбница шла и его открытость, массовая популяризация новых идей, что Ньютон делал крайне неохотно.
Слайд 10Работы Лейбница по математике многочисленны и разнообразны.
В 1666 году он написал
первое сочинение: «О комбинаторном искусстве». Сейчас комбинаторика и теория вероятности одна из обязательных тем математики в школе.
Слайд 11В1672 году Лейбниц изобретает собственную конструкцию арифмометра, гораздо лучше паскалевской —
он умел выполнять умножение, деление и извлечение корней. Предложенные им ступенчатый валик и подвижная каретка легли в основу всех последующих арифмометров.
Лейбниц также описал двоичную систему счисления с цифрами 0 и 1, на которой основана современная компьютерная техника.
Лейбниц также описал двоичную систему счисления с цифрами 0 и 1, на которой основана современная компьютерная техника.
Слайд 12Производной функции у = f(x), заданной на некотором интервале (a; b),
в некоторой точке х этого интервала называют предел отношения приращения функции в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.
Слайд 15Правила нахождения производной
1. Если функции u(x) и v(x) имеют в точке
х производные, то их сумма u(x) + v(x) также имеет в этой точке производную, причем
(u + v)′ = u′ + v′
2. Если функция u(x) имеет в точке х производную и С – данное число, то функция С∙u(x) также имеет в этой точке производную, причем
(Сu)′ = С∙u′
Слайд 16Правила нахождения производной
3. Если функции u(x) и v(x) имеют в точке
х производные, то их произведение u(x) ∙ v(x) также имеет в этой точке производную, причем
(u ∙ v)′ = u′∙v + u∙v′
4. Если функция v(x) имеет в точке х производную и v(x) ≠ 0, то функция также имеет в этой точке производную, причем
Слайд 17Правила нахождения производной
5. Если функции u(x) и v(x) имеют в точке
х производные и v(x) ≠ 0, то функция также имеет в этой точке производную, причем
6.Производная сложной функции
(f(g(x)))′ = f′(g(x))∙g′(x)
Слайд 20подсказка
Тело, подброшенное вверх движется по закону
s(t) = 4+ 8t
– 5t 2 . Найдите:
1) Скорость тела в начальный момент времени;
2) Наибольшую высоту подъёма тела.
1) Скорость тела в начальный момент времени;
2) Наибольшую высоту подъёма тела.
РЕШЕНИЕ.
2) t= 0, v(0) = s`(0) = 8 м/с – скорость
тела в начальный момент времени
1) v (t) = s` (t) = 8 – 10t - скорость тела;
3) s (0,8)= 4+ 8·0,8 – 5· 0,64 =7,2 м – максимальная высота броска тела.
Ответ: 8 м/с ; 7,2 м .
ЗАДАЧА №1
Слайд 22“При изучении наук примеры не менее поучительны, нежели правила”
“Примеры
учат
больше, чем теория”.
И. Ньютон
М. Ломоносов
Слайд 26Правильный
ответ
Правильный
ответ
Правильный
ответ
Правильный
ответ
Правильный
ответ
Найдите производные функций:
Слайд 27Найдите производную функции(устно):
а) у = 6х5 – 7х3 + 2х2 –
5,
у/ = 30 х4 – 21х2 + 4х ,
б) у = (4 – 5х)7,
у/ = 7·(– 5)·(4 – 5х)6 = – 35·(4 – 5х)6
в) у = 8 + 3cosх,
у/ = 8 – 3sinх
г) у = 4sinх – 6 lnx,
у/ = 4 cos х – 6/х
у/ = 30 х4 – 21х2 + 4х ,
б) у = (4 – 5х)7,
у/ = 7·(– 5)·(4 – 5х)6 = – 35·(4 – 5х)6
в) у = 8 + 3cosх,
у/ = 8 – 3sinх
г) у = 4sinх – 6 lnx,
у/ = 4 cos х – 6/х
Правильный
ответ
Правильный
ответ
Правильный
ответ
Правильный
ответ
Слайд 28Найдите производную функции(устно):
Правильный
ответ
Правильный
ответ
Правильный
ответ
Правильный
ответ
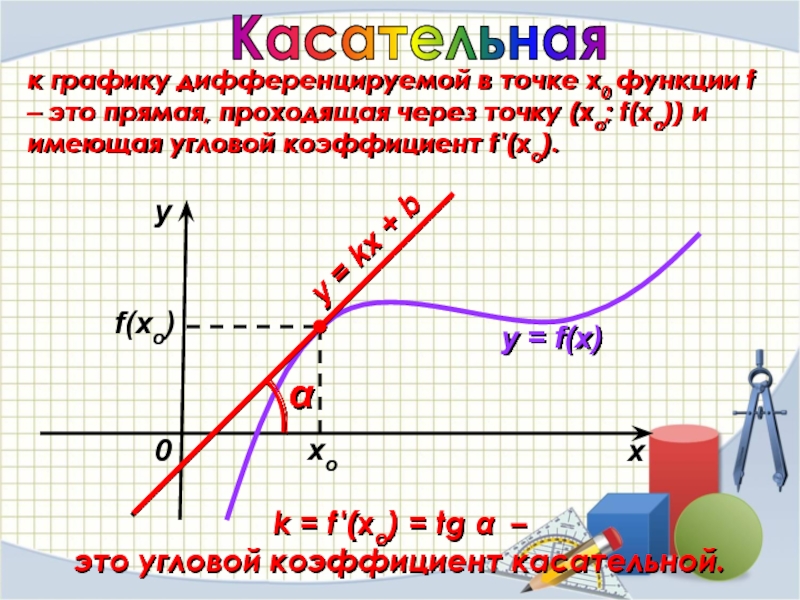
Слайд 31k = f ′(xo) = tg α –
это угловой коэффициент
касательной.
f(xo)
Касательная
к графику дифференцируемой в точке х0 функции f – это прямая, проходящая через точку (хо; f(xо)) и имеющая угловой коэффициент f ′(хо).
х
у
хо
y = kx + b
α
y = f(x)
0
Слайд 32Общий вид уравнения касательной
y = f ′(xo)(x – xo) + f(xo)
Алгоритм
составления уравнения касательной
1о Находим значение функции в точке хо: f(xo).
2о Дифференцируем функцию: f′(x).
3о Находим значение производной в точке хо: f′(xo).
4о Подставляем эти данные в общее уравнения
касательной: y = f′(xo)(x – xo) + f(xo).
Слайд 33Одна из основных задач исследования функции – это нахождение промежутков её
возрастания и убывания.
Признак возрастания функции:
Если f´(x)>0 в каждой точке интервала I, то функция f возрастает на I.
Признак убывания функции:
Если f´(x)<0 в каждой точке интервала I, то функция f убывает на I.
Признак возрастания функции:
Если f´(x)>0 в каждой точке интервала I, то функция f возрастает на I.
Признак убывания функции:
Если f´(x)<0 в каждой точке интервала I, то функция f убывает на I.
Слайд 34Алгоритм решения неравенств методом интервалов:
Выделить функцию y=f(x).
Найти область определения функции D(f).
Указать промежутки непрерывности.
Найти нули функции, решив уравнение f(x)=0.
Определить знак функции между
её нулями в области определения.
Найти нули функции, решив уравнение f(x)=0.
Определить знак функции между
её нулями в области определения.
Слайд 36Алгоритм нахождения промежутков возрастания (убывания) функции y=f(x):
Найти производную функции f´(x).
Решить
уравнение f´ (x) =0.
Найти знак производной на каждом интервале.
Согласно признаку возрастания (убывания) функции, найти промежутки возрастания и убывания.
Найти знак производной на каждом интервале.
Согласно признаку возрастания (убывания) функции, найти промежутки возрастания и убывания.
Слайд 38f′(x)
xo
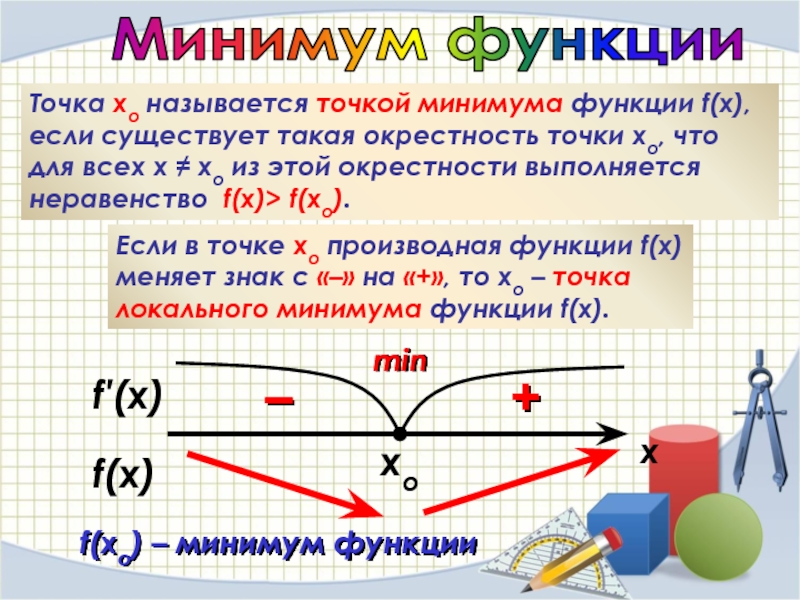
Минимум функции
Точка хо называется точкой минимума функции f(x), если существует такая
окрестность точки хо, что для всех х ≠ хо из этой окрестности выполняется неравенство f(x)> f(xo).
Если в точке хо производная функции f(x) меняет знак с «–» на «+», то хо – точка локального минимума функции f(x).
f(x)
–
+
x
min
f(xо) – минимум функции
Слайд 39xo
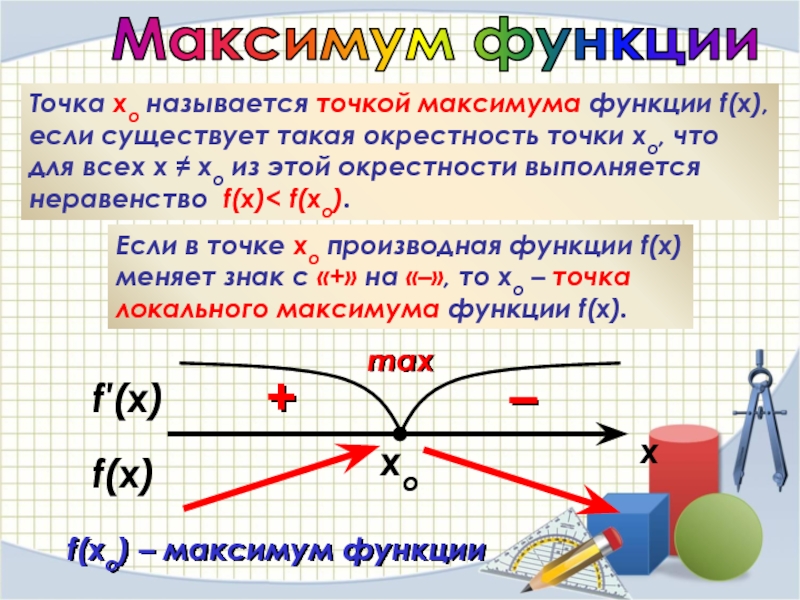
Максимум функции
Точка хо называется точкой максимума функции f(x), если существует такая
окрестность точки хо, что для всех х ≠ хо из этой окрестности выполняется неравенство f(x)< f(xo).
Если в точке хо производная функции f(x) меняет знак с «+» на «–», то хо – точка локального максимума функции f(x).
f′(x)
f(x)
+
–
x
max
f(xо) – максимум функции
Слайд 40Алгоритм исследования
функции на монотонность
1о Дифференцируем функцию: f′(x).
2о Находим
критические точки из уравнения: f′(x) = 0.
3о Решаем неравенства: f′(x) > 0 и f′(x) < 0.
4о Полученные данные изображаем на схеме:
3о Решаем неравенства: f′(x) > 0 и f′(x) < 0.
4о Полученные данные изображаем на схеме:
5o a) Промежутки возрастания: (– ∞; х1]; [x2; x3].
б) Промежутки убывания: [x1; x2]; [x3; + ∞).
f′(x)
x2
f(x)
–
+
x
+
–
x1
x3
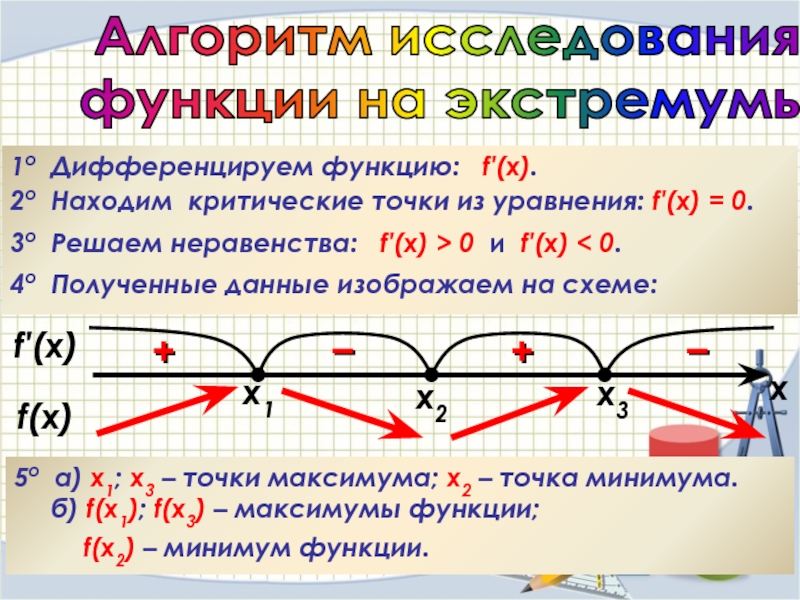
Слайд 41Алгоритм исследования
функции на экстремумы
1о Дифференцируем функцию: f′(x).
2о Находим
критические точки из уравнения: f′(x) = 0.
3о Решаем неравенства: f′(x) > 0 и f′(x) < 0.
4о Полученные данные изображаем на схеме:
3о Решаем неравенства: f′(x) > 0 и f′(x) < 0.
4о Полученные данные изображаем на схеме:
5o a) х1; x3 – точки максимума; x2 – точка минимума.
б) f(x1); f(x3) – максимумы функции;
f(x2) – минимум функции.
f′(x)
x2
f(x)
–
+
x
+
–
x1
x3
