Математике
Тема: Понятие функции, ее свойства и способы задания»
по Математике
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Понятие и свойства функции
Содержание
- 1. Презентация по математике на тему: Понятие и свойства функции
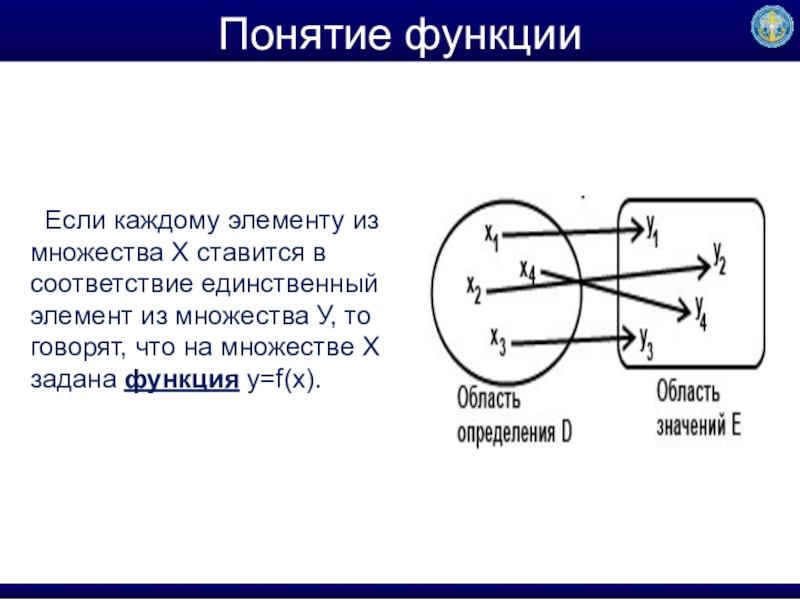
- 2. Понятие функции Если каждому элементу из множества
- 3. Способы задания функцийАналитическийГрафическийТабличныйОписательный
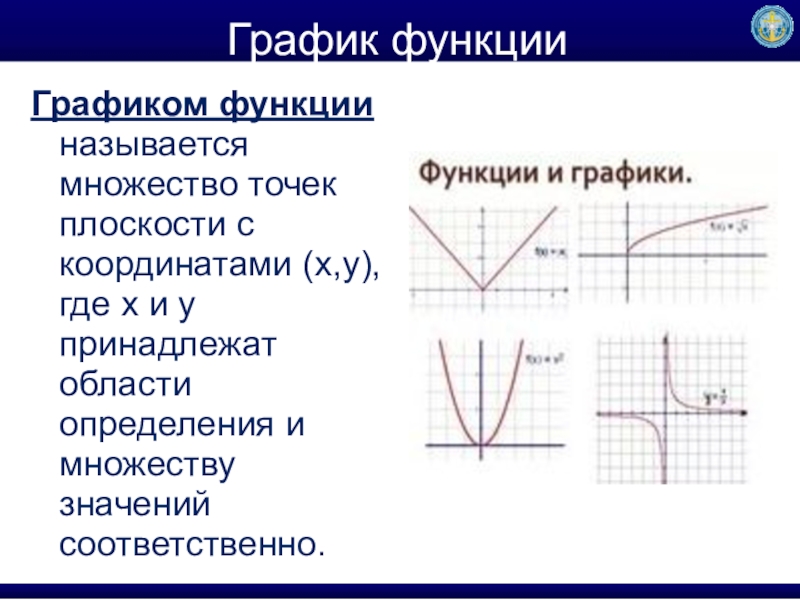
- 4. График функции Графиком функции называется множество точек
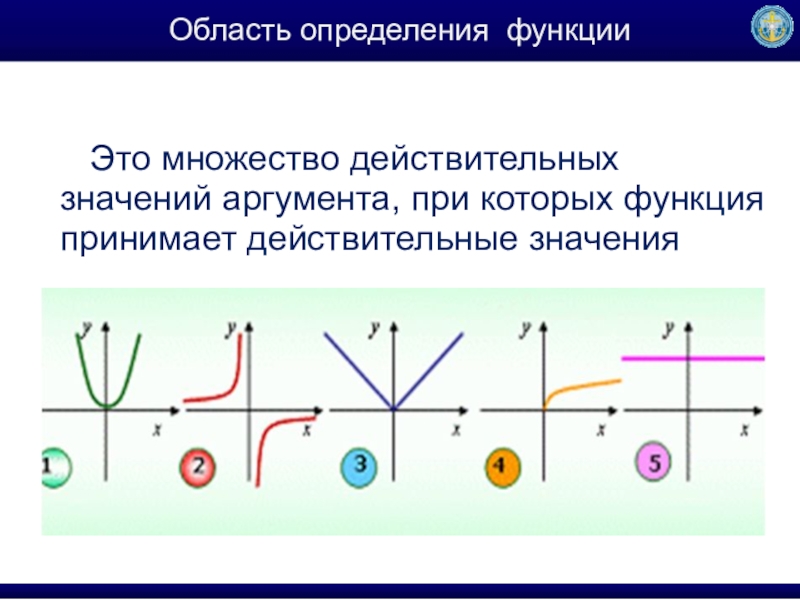
- 5. Область определения функцииЭто множество действительных значений аргумента, при которых функция принимает действительные значения
- 6. Различные случаи нахождения области определения функции1. Дробное
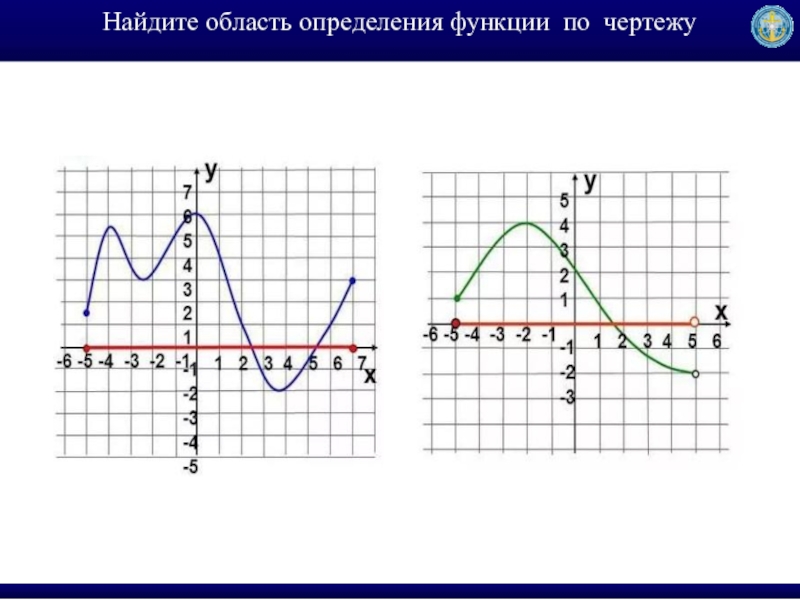
- 7. Найдите область определения функции по чертежу
- 8. Найти область определения функции:
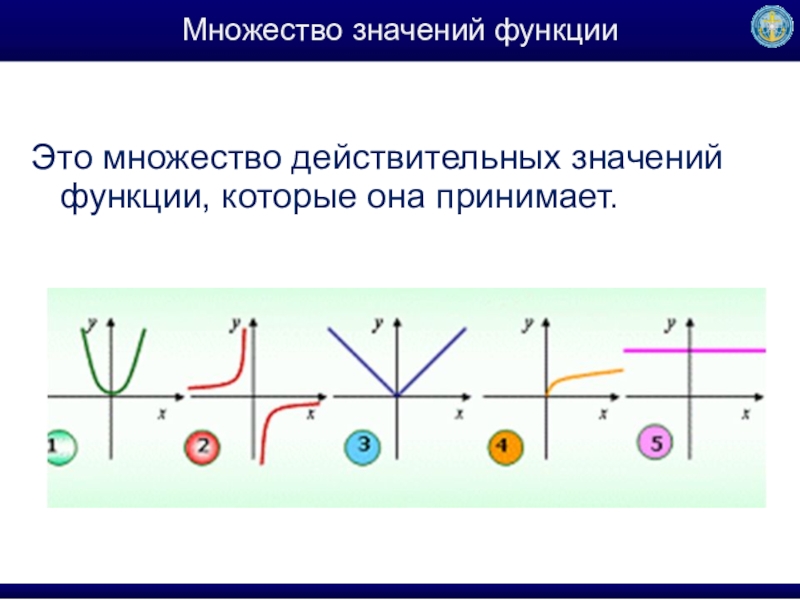
- 9. Множество значений функцииЭто множество действительных значений функции, которые она принимает.
- 10. К основным свойствам функции относят:Четность/нечетностьВозрастание/убываниеВыпуклость/вогнутостьОграниченностьПромежутки знакопостоянства
- 11. Функция называется четной, если:Функция называется нечетной, если:1.
- 12. Функция общего видаЕсли функция определена на симметричном
- 13. Исследовать на четность/нечетность функции:
- 14. Монотонность функцииФункция называется возрастающей, если:Большему значению аргумента
- 15. МонотонностьПромежутки, на которых функция либо монотонно возрастает либо монотонно убывает, называются промежутками монотонности
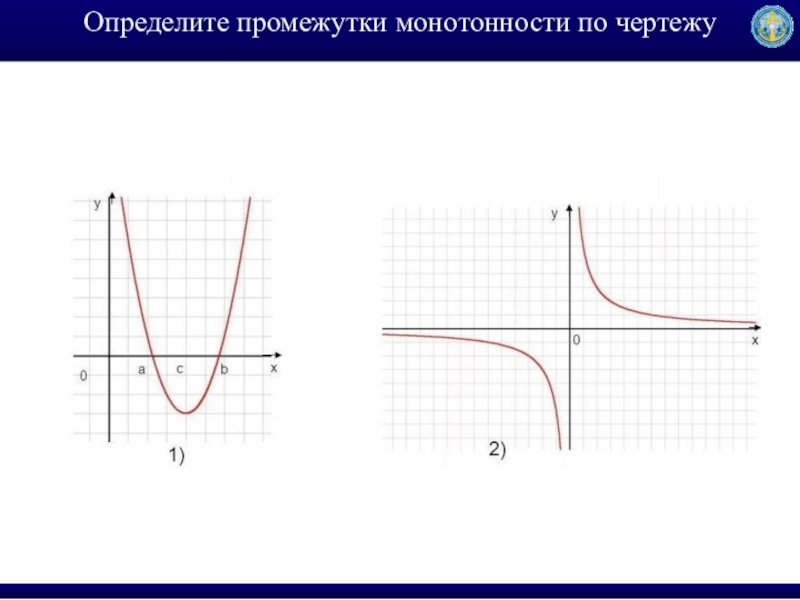
- 16. Определите промежутки монотонности по чертежу
- 17. Направление выпуклостиЕсли при соединении двух точек графика
- 18. Направление выпуклости
- 19. Понятие ограниченностиФункцию у=f(x) называют ограниченной сверху
- 20. Понятие ограниченностиФункцию y=f(x) называют ограниченной на множестве
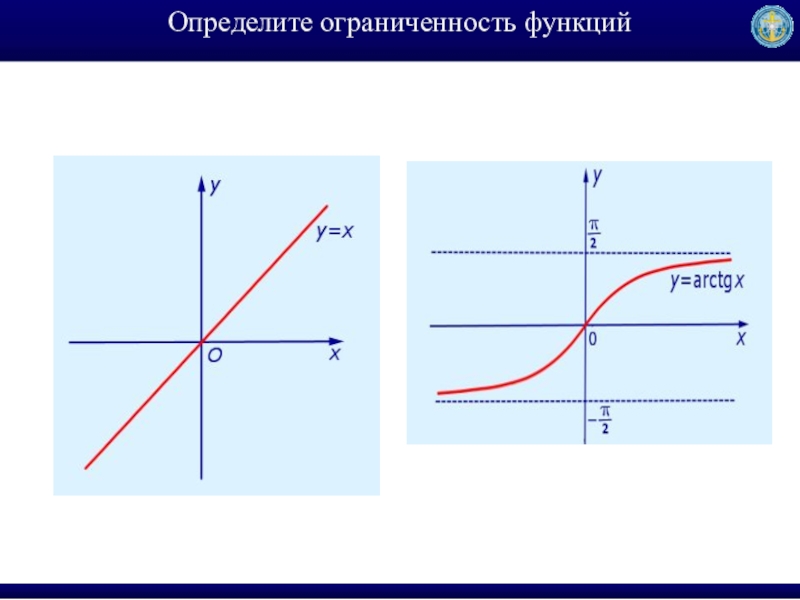
- 21. Определите ограниченность функций
- 22. Промежутки знакопостоянстваПромежутки знакопостоянства — такие промежутки на
- 23. Основные виды преобразования графиков функций
Понятие функции Если каждому элементу из множества Х ставится в соответствие единственный элемент из множества У, то говорят, что на множестве Х задана функция у=f(x).
Слайд 1Автор: Зеленская О.Ю.
ДДополнительная образовательная программа
«Подготовительный курс для абитуриентов колледжа» по
Слайд 2Понятие функции
Если каждому элементу из множества Х ставится в соответствие
единственный элемент из множества У, то говорят, что на множестве Х задана функция у=f(x).
Слайд 4График функции
Графиком функции называется множество точек плоскости с координатами (х,у),
где х и у принадлежат области определения и множеству значений соответственно.
Слайд 5Область определения функции
Это множество действительных значений аргумента, при которых функция принимает
действительные значения
Слайд 6Различные случаи нахождения области определения функции
1. Дробное выражение
2. Выражение, содержащее переменную
под знаком корня четной степени
3. Дробное выражение, содержащее переменную в знаменателе под знаком корня четной степени
3. Дробное выражение, содержащее переменную в знаменателе под знаком корня четной степени
Слайд 9Множество значений функции
Это множество действительных значений функции, которые она принимает.
Слайд 10К основным свойствам функции относят:
Четность/нечетность
Возрастание/убывание
Выпуклость/вогнутость
Ограниченность
Промежутки знакопостоянства
Слайд 11
Функция называется четной, если:
Функция называется нечетной, если:
1. Она определена на симметричном
относительно нуля промежутке
2. Выполняется условие
f(-x)=f(x)
График четной функции проходит симметрично относительно оси Ох.
2. Выполняется условие
f(-x)=f(x)
График четной функции проходит симметрично относительно оси Ох.
1. Она определена на симметричном относительно нуля промежутке
2. Выполняется условие
f(-x)=-f(x)
График нечетной функции проходит симметрично относительно начала координат.
Слайд 12Функция общего вида
Если функция определена на симметричном относительно нуля промежутке и
не выполняются условия
f(-x)=f(x) и f(-x)=-f(x),
то фунция у= f(x) является ни четной и ни нечетной или функцией общего вида.
f(-x)=f(x) и f(-x)=-f(x),
то фунция у= f(x) является ни четной и ни нечетной или функцией общего вида.
Слайд 14Монотонность функции
Функция называется возрастающей, если:
Большему значению аргумента соответствует большее значение функции.
Функция
называется убывающей, если:
Большему значению аргумента соответствует меньшее значение функции.
Слайд 15Монотонность
Промежутки, на которых функция либо монотонно возрастает либо монотонно убывает, называются
промежутками монотонности
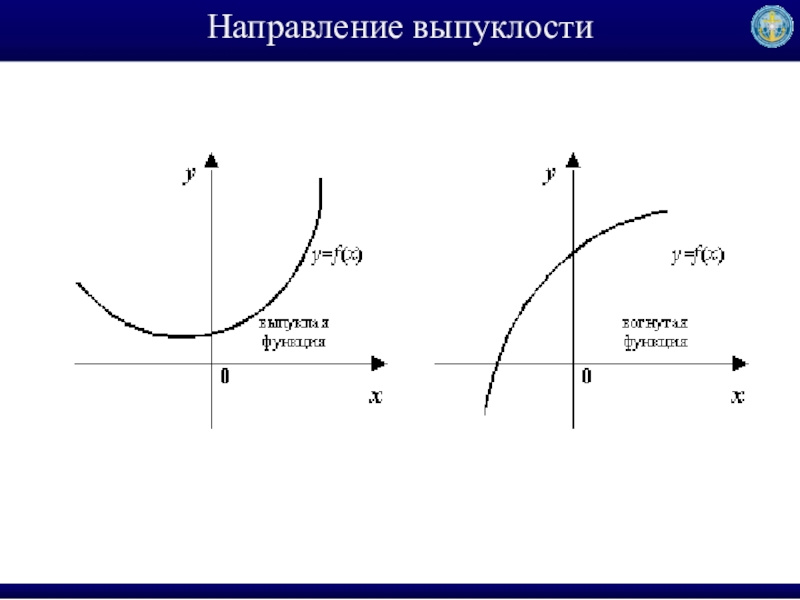
Слайд 17Направление выпуклости
Если при соединении двух точек графика функции у=f(x) отрезком, обнаружится,
что
соответствующая часть графика лежит ниже проведенного отрезка, то говорят, что функция выпукла вниз;
соответствующая часть графика лежит выше проведенного отрезка, то говорят, что функция выпукла вверх.
соответствующая часть графика лежит ниже проведенного отрезка, то говорят, что функция выпукла вниз;
соответствующая часть графика лежит выше проведенного отрезка, то говорят, что функция выпукла вверх.
Слайд 19Понятие ограниченности
Функцию у=f(x) называют ограниченной сверху на множестве X,
если существует такое число a , что для любого x из множества X выполнено неравенство
f(x)≤a
f(x)≤a
Функцию у=f(x) называют ограниченной снизу на множестве X, если существует такое число b , что для любого x из множества X выполнено неравенство
f(x)≥b
Слайд 20Понятие ограниченности
Функцию y=f(x) называют ограниченной на множестве X , если
существуют такие числа a и b , что для любого x из множества X выполнено неравенство
a≤f(x)≤b
a≤f(x)≤b
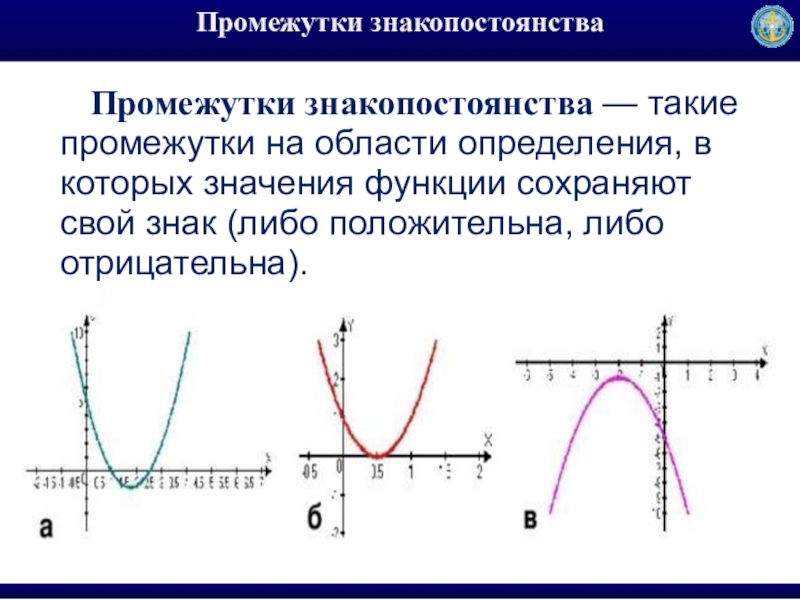
Слайд 22Промежутки знакопостоянства
Промежутки знакопостоянства — такие промежутки на области определения, в которых
значения функции сохраняют свой знак (либо положительна, либо отрицательна).
