- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Параллельное проектирование
Содержание
- 1. Презентация по математике на тему Параллельное проектирование
- 2. Проектирование пространства на плоскость α параллельно направлению,
- 3. Свойства параллельного проектирования.Если точка Рєα,то f(P)=P’=P. Действительно,
- 4. 5. Пусть АВ и СD – два
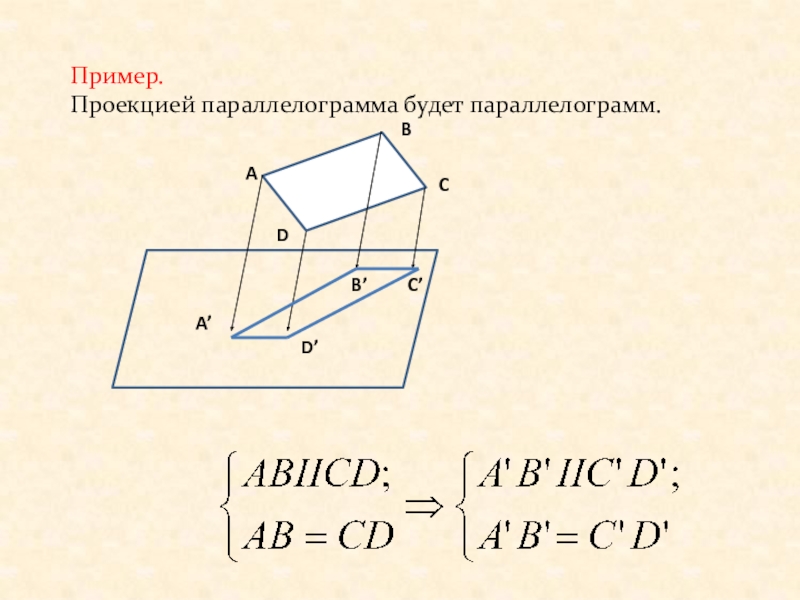
- 5. Пример. Проекцией параллелограмма будет параллелограмм.ABCDA’D’B’C’
- 6. Площадь ортогональной проекции многоугольникаТеорема. Пусть многоугольник F
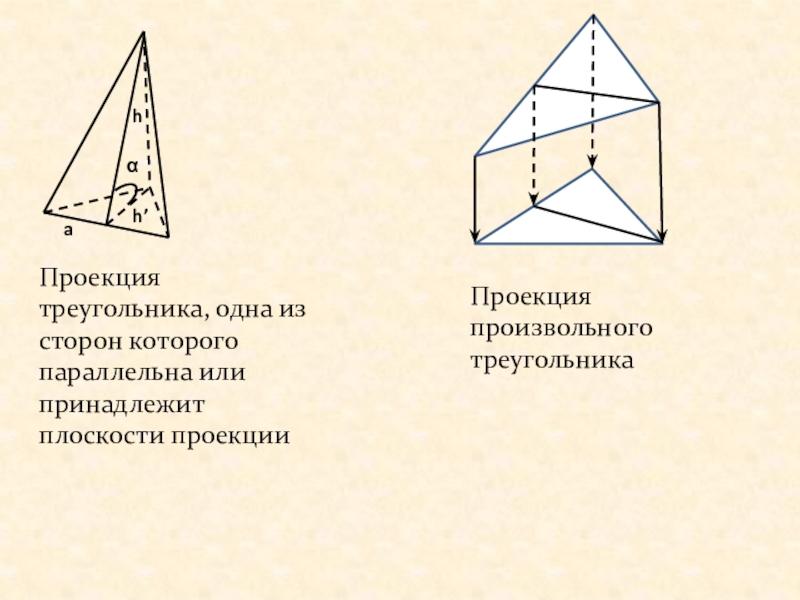
- 7. h’ahαПроекция треугольника, одна из сторон которого параллельна или принадлежит плоскости проекцииПроекция произвольного треугольника
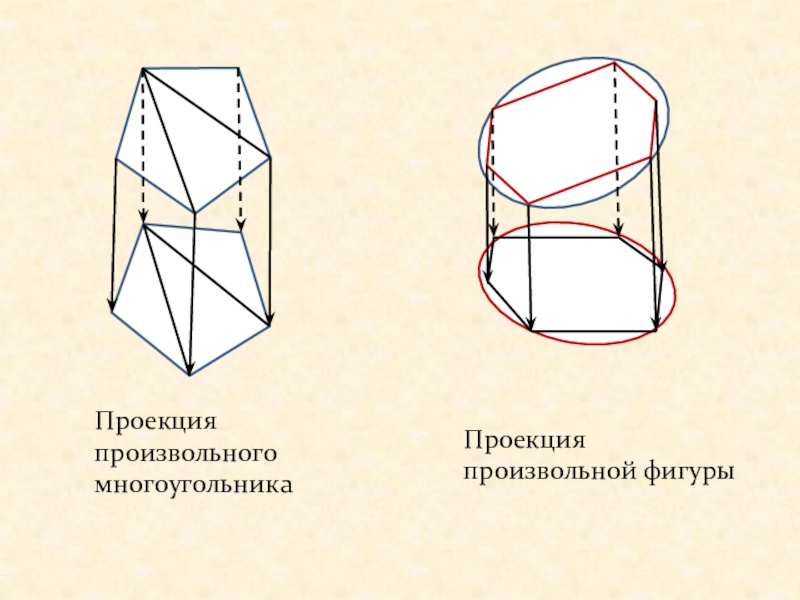
- 8. Проекция произвольного многоугольникаПроекция произвольной фигуры
Проектирование пространства на плоскость α параллельно направлению, задаваемому прямой l, пересекающей плоскость α, - это преобразование, при котором каждая точка А вне плоскости α переходит в точку А’, лежащую в плоскости α и такую, что прямая
Слайд 2Проектирование пространства на плоскость α параллельно направлению, задаваемому прямой l, пересекающей
плоскость α, - это преобразование, при котором каждая точка А вне плоскости α переходит в точку А’, лежащую в плоскости α и такую, что прямая АА’ параллельна прямой l, а точки плоскости α остаются неподвижными.
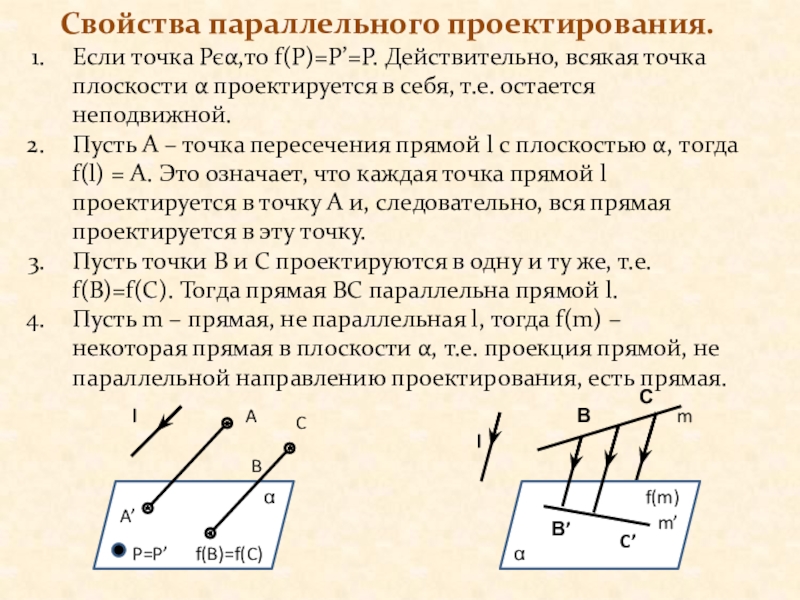
Слайд 3Свойства параллельного проектирования.
Если точка Рєα,то f(P)=P’=P. Действительно, всякая точка плоскости α
проектируется в себя, т.е. остается неподвижной.
Пусть А – точка пересечения прямой l с плоскостью α, тогда f(l) = A. Это означает, что каждая точка прямой l проектируется в точку А и, следовательно, вся прямая проектируется в эту точку.
Пусть точки В и С проектируются в одну и ту же, т.е. f(В)=f(C). Тогда прямая BC параллельна прямой l.
Пусть m – прямая, не параллельная l, тогда f(m) – некоторая прямая в плоскости α, т.е. проекция прямой, не параллельной направлению проектирования, есть прямая.
Пусть А – точка пересечения прямой l с плоскостью α, тогда f(l) = A. Это означает, что каждая точка прямой l проектируется в точку А и, следовательно, вся прямая проектируется в эту точку.
Пусть точки В и С проектируются в одну и ту же, т.е. f(В)=f(C). Тогда прямая BC параллельна прямой l.
Пусть m – прямая, не параллельная l, тогда f(m) – некоторая прямая в плоскости α, т.е. проекция прямой, не параллельной направлению проектирования, есть прямая.
α
P=P’
f(B)=f(C)
В
α
f(m)
m’
m
С
В’
C’
l
l
A’
A
C
B
Слайд 45. Пусть АВ и СD – два параллельных (или лежащих на
одной прямой) отрезка. Считаем, что АВ и СD не параллельны прямой l. Пусть они проектируются в отрезки А’B’ и C’D’. Параллельное проектирование параллельных отрезков сохраняет их параллельность и отношение их длин.
l
ABIICD => A’B’IIC’D’;
AB/CD=A’B’/C’D’
A
A’
B
B’
C
C’
D
D’
6. Проекция середины отрезка есть середина проекции отрезка.
l
A
M
B
B’
M’
A’
AM=MB=>A’M’=M’B’
Слайд 6Площадь ортогональной проекции многоугольника
Теорема. Пусть многоугольник F расположен в плоскости α,
образующей угол φ с плоскостью β. Тогда площадь ортогональной проекции F’ многоугольника F на плоскость β равна исходной площади, умноженной на cosφ: S(F’)=S(F)cosφ
α
β
φ
F
F’
Слайд 7h’
a
h
α
Проекция треугольника, одна из сторон которого параллельна или принадлежит плоскости проекции
Проекция
произвольного треугольника