- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Палиндромы в математике (5-7 классы)
Содержание
- 1. Презентация по математике на тему Палиндромы в математике (5-7 классы)
- 2. Актуальность выбора темыЧисла палиндромы образуют одно из
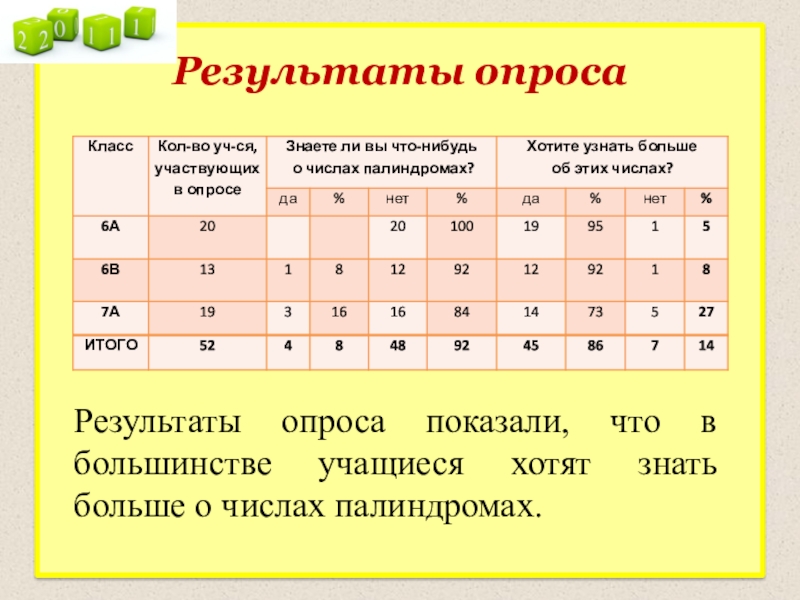
- 3. Результаты опросаРезультаты опроса показали, что в большинстве учащиеся хотят знать больше о числах палиндромах.
- 4. Гипотеза Простые числа – это часть
- 5. Цель исследования Изучить свойства особенных чисел
- 6. Числа палиндромы ШАЛАШРАДАРТОПОТКОККАЗАК
- 7. Числовые палиндромы это натуральные числа, которые
- 8. Алгоритм получения палиндромаВозьми любое двузначное числоПереверни
- 9. Свойства палиндромовСуществует единственный простой палиндром с чётным
- 10. Свойства палиндромовВсе однозначные числа являются палиндромами.26 –
- 11. Свойства палиндромовИз простых чисел - палиндромов, располагая
- 12. Формулы – палиндромыПод формулами – палиндромами понимают
- 13. Задача 1Найти все пары таких двузначных чисел,
- 14. РешениеПредставим наши числа в виде суммы разрядных
- 15. Задача 2Найти все пары таких двузначных чисел,
- 16. РешениеПредставим наши числа в виде суммы разрядных
- 17. Задача 3Найти все пары таких двузначных чисел,
- 18. РешениеПредставим наши числа в виде суммы разрядных
- 19. Задача 4Найти все пары таких двузначных чисел,
- 20. Практическая частьЗадача 1. Приведите примеры того, как
- 21. Практическая частьЗадача 2. Докажите, что если из
- 22. Практическая частьЗадача 3. (Б.А. Кордемский «Математическая смекалка»)Найти
- 23. Примеры палиндромовВ русском языке:Утречко летело к чертуЯ
- 24. Примеры палиндромовМагический квадратДревнейший из сохранившихся палиндромов написан
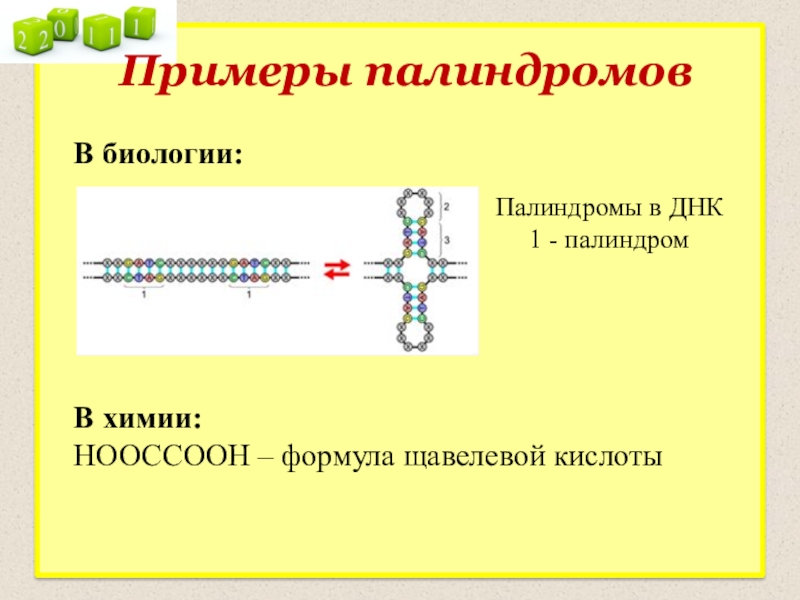
- 25. Примеры палиндромовВ биологии:Палиндромы в ДНК
- 26. Примеры палиндромовВ изобразительном искусстве:
- 27. ЗаключениеЯ познакомилась с удивительными натуральными числами -
- 28. Всем спасибо за внимание! 1 x
Актуальность выбора темыЧисла палиндромы образуют одно из наиболее интересных подмножеств множества натуральных чисел. Они обладают необычной историей, удивительными свойствами.
Слайд 1Палиндромы
в математике
Автор: ученица 7А класса
Ярдыкова Карина
Руководитель: учитель математики
Михайлова Тамара Александровна
Слайд 2Актуальность выбора темы
Числа палиндромы образуют одно из наиболее интересных подмножеств множества
натуральных чисел. Они обладают необычной историей, удивительными свойствами.
Слайд 3Результаты опроса
Результаты опроса показали, что в большинстве учащиеся хотят знать больше
о числах палиндромах.
Слайд 4
Гипотеза
Простые числа – это часть чисел, из которых состоят все натуральные
числа.
Исследуя множество простых чисел, можно получить удивительные числовые множества с их необыкновенными свойствами.
Исследуя множество простых чисел, можно получить удивительные числовые множества с их необыкновенными свойствами.
Слайд 5
Цель исследования
Изучить свойства особенных чисел - палиндромов и научиться решать с
их помощью некоторые математические задачи на смекалку олимпиадного характера.
Слайд 7Числовые палиндромы
это натуральные числа, которые одинаково читаются справа налево
и слева направо. Иначе говоря, отличаются симметрией записи (расположения цифр), причём число знаков может быть как чётным, так и нечётным.
121; 676; 1331; 4884; 94949; 1177711; 1178711 и т. д.
121; 676; 1331; 4884; 94949; 1177711; 1178711 и т. д.
Слайд 8Алгоритм
получения палиндрома
Возьми любое двузначное число
Переверни его (переставь цифры справа налево)
Найди
их сумму
Переверни полученное число
Найди их сумму
Повторяй аналогичные действия до тех пор, пока не получится палиндром
Переверни полученное число
Найди их сумму
Повторяй аналогичные действия до тех пор, пока не получится палиндром
Пример:
96
96 + 69 = 165
165 + 561 = 726
726 + 627 = 1353
1353 + 3531 = 4884
Слайд 9Свойства палиндромов
Существует единственный простой палиндром с чётным числом цифр – 11.
Первой
и последней цифрами любого простого палиндрома могут быть только 1; 3; 7 или 9.
Например: 13 и 31; 17 и 71; 37 и 73; 79 и 97
Среди простых трёхзначных палиндромов встречаются пары чисел, у которых средняя цифра отличается всего на 1.
Например: 181 и 191; 373 и 383; 787 и 797; 919 и 929
Аналогичная картина наблюдается у больших простых чисел.
Например: 94849 и 94949; 1177711 и 1178711
Например: 13 и 31; 17 и 71; 37 и 73; 79 и 97
Среди простых трёхзначных палиндромов встречаются пары чисел, у которых средняя цифра отличается всего на 1.
Например: 181 и 191; 373 и 383; 787 и 797; 919 и 929
Аналогичная картина наблюдается у больших простых чисел.
Например: 94849 и 94949; 1177711 и 1178711
Слайд 10Свойства палиндромов
Все однозначные числа являются палиндромами.
26 – наименьшее число, не являющееся
палиндромом, квадрат которого палиндром: 26² = 676
А вот пары чисел - «перевёртышей» 13 — 31 и 113 — 311 при возведении в квадрат дают также пары «перевёртышей»: 169 — 961 и 12769 — 96721. Любопытно, что даже суммы их цифр, оказались, связаны хитрым образом:
(1 + 3)2 = 1 + 6 + 9,
(1 + 1 + 3)2 = 1 + 2 + 7 + 6 + 9.
А вот пары чисел - «перевёртышей» 13 — 31 и 113 — 311 при возведении в квадрат дают также пары «перевёртышей»: 169 — 961 и 12769 — 96721. Любопытно, что даже суммы их цифр, оказались, связаны хитрым образом:
(1 + 3)2 = 1 + 6 + 9,
(1 + 1 + 3)2 = 1 + 2 + 7 + 6 + 9.
Слайд 11Свойства палиндромов
Из простых чисел - палиндромов, располагая их определённым образом, скажем
построчно, можно составить симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр.
Слайд 12Формулы – палиндромы
Под формулами – палиндромами понимают выражение, состоящее из суммы
или разности, произведения или частного чисел, результат которого не меняется в результате прочтения выражения справа налево.
Например:
42 + 35 = 53 + 24
41 – 32 = 23 – 14
63 ∙ 48 = 84 ∙ 36
82 : 41 = 28 : 14
Слайд 13Задача 1
Найти все пары таких двузначных чисел, чтобы результат их сложения
не менялся в результате прочтения суммы справа налево, т.е.
x1y1 + x2y2 = y2x2 + y1x1
x1y1 + x2y2 = y2x2 + y1x1
Слайд 14Решение
Представим наши числа в виде суммы разрядных слагаемых:
(10х1 + у1) +
(10х2 + у2) = (10у2 + х2) + (10у1 + х1)
10х1 + у1 + 10х2 + у2 = 10у2 + х2 +10у1 + х1
10х1 - х1 + 10х2 - х2 = 10у1 - у1 + 10у2 - у2
9х1 + 9х2 = 9у1 + 9у2
9(х1 + х2) = 9(у1 + у2)
х1 + х2 = у1 + у2.
Вывод: Для решения этой задачи сумма первых цифр должна быть равна сумме их вторых цифр, т.е.
х1 + х2 = у1 + у2.
Примеры:
76 + 34 = 43 + 67
25 + 63 = 36 + 52 и т.д.
10х1 + у1 + 10х2 + у2 = 10у2 + х2 +10у1 + х1
10х1 - х1 + 10х2 - х2 = 10у1 - у1 + 10у2 - у2
9х1 + 9х2 = 9у1 + 9у2
9(х1 + х2) = 9(у1 + у2)
х1 + х2 = у1 + у2.
Вывод: Для решения этой задачи сумма первых цифр должна быть равна сумме их вторых цифр, т.е.
х1 + х2 = у1 + у2.
Примеры:
76 + 34 = 43 + 67
25 + 63 = 36 + 52 и т.д.
Слайд 15Задача 2
Найти все пары таких двузначных чисел, чтобы результат их вычитания
не менялся в результате прочтения разности справа налево, т.е.
x1y1 - x2y2 = y2x2 - y1x1
x1y1 - x2y2 = y2x2 - y1x1
Слайд 16Решение
Представим наши числа в виде суммы разрядных слагаемых:
(10х1 + у1) –
(10х2 + у2) = (10у2 + х2) – (10у1 + х1)
10х1 + у1 – 10х2 - у2 = 10у2 + х2 – 10у1 - х1
10х1 + х1 + у1 + 10у1 = 10у2 + у2 + 10х2 + х2
11 х1 + 11 у1 = 11х2 + 11у2
11(х1 + у1) = 11(х2 + у2)
х1 + у1 = х2 + у2
Вывод: Для решения этой задачи у таких чисел должны быть равны суммы цифр, т.е.
х1 + у1 = х2 + у2
Примеры:
46 – 28 = 82 – 64
52 –16 = 61 – 25 и т.д.
10х1 + у1 – 10х2 - у2 = 10у2 + х2 – 10у1 - х1
10х1 + х1 + у1 + 10у1 = 10у2 + у2 + 10х2 + х2
11 х1 + 11 у1 = 11х2 + 11у2
11(х1 + у1) = 11(х2 + у2)
х1 + у1 = х2 + у2
Вывод: Для решения этой задачи у таких чисел должны быть равны суммы цифр, т.е.
х1 + у1 = х2 + у2
Примеры:
46 – 28 = 82 – 64
52 –16 = 61 – 25 и т.д.
Слайд 17Задача 3
Найти все пары таких двузначных чисел, чтобы результат их деления
не менялся в результате прочтения частного справа налево, т.е.
x1y1 ∙ x2y2 = y2x2 ∙ y1x1
x1y1 ∙ x2y2 = y2x2 ∙ y1x1
Слайд 18Решение
Представим наши числа в виде суммы разрядных слагаемых:
(10х1 + у1) ∙
(10х2 + у2) = (10у2 + х2) ∙ (10у1 + х1)
100х1∙х2 + 10х1∙у2 + 10у1∙х2 + у1∙у2 = 100у1∙у2 + 10х1∙у2 + 10у1∙х2 + х1∙х2
99х1∙х2 = 99у1∙у2
х1∙х2 = у1∙у2
Вывод: Для решения этой задачи произведение первых цифр чисел равно произведению их вторых цифр, т.е.
х1∙х2 = у1∙у2
Примеры:
82 ∙ 14 = 41 ∙ 28
46 ∙ 32 = 23 ∙ 64 и т.д.
100х1∙х2 + 10х1∙у2 + 10у1∙х2 + у1∙у2 = 100у1∙у2 + 10х1∙у2 + 10у1∙х2 + х1∙х2
99х1∙х2 = 99у1∙у2
х1∙х2 = у1∙у2
Вывод: Для решения этой задачи произведение первых цифр чисел равно произведению их вторых цифр, т.е.
х1∙х2 = у1∙у2
Примеры:
82 ∙ 14 = 41 ∙ 28
46 ∙ 32 = 23 ∙ 64 и т.д.
Слайд 19Задача 4
Найти все пары таких двузначных чисел, чтобы результат их деления
не менялся в результате прочтения чисел справа налево.
Для решения этой задачи произведение первой цифры первого числа на вторую цифру второго числа равно произведению двух других их цифр, т.е.
x1 ∙ y2 = x2 ∙ y1
Примеры:
82 : 41 = 28 : 14
62 : 31 = 26 : 13
Для решения этой задачи произведение первой цифры первого числа на вторую цифру второго числа равно произведению двух других их цифр, т.е.
x1 ∙ y2 = x2 ∙ y1
Примеры:
82 : 41 = 28 : 14
62 : 31 = 26 : 13
Слайд 20Практическая часть
Задача 1.
Приведите примеры того, как при помощи одних палиндромов
получаются другие:
Решение.
а) 212² - 121² = 44944 – 14641 = 30303;
б) 2·121·10201 = 2·11² ·101² = 22·112211 = 1111· 2222 = 2468642.
Решение.
а) 212² - 121² = 44944 – 14641 = 30303;
б) 2·121·10201 = 2·11² ·101² = 22·112211 = 1111· 2222 = 2468642.
Слайд 21Практическая часть
Задача 2.
Докажите, что если из трёхзначного числа вычесть число,
записанное теми же цифрами, но в обратном порядке, разность всегда будет делиться на 9.
Решение.
Ответ: Данное произведение делится на 9.
Решение.
Ответ: Данное произведение делится на 9.
Слайд 22Практическая часть
Задача 3. (Б.А. Кордемский «Математическая смекалка»)
Найти 10-тизначное число с неповторяющимися
цифрами, при делении которого на 9 получается в частном палиндромическое число, т.е. читающееся одинаково как слева направо, так и справа налево.
Вот первые результаты моей работы:
8 706 543 921 : 9 = 967 393 769
1 206 453 879 : 9 = 134 050 431
4 059 721 386 : 9 = 451 080 154
Таких 10-тизначных чисел с неповторяющимися цифрами более трёх миллионов: 9/10*10!=3 265 920
Вот первые результаты моей работы:
8 706 543 921 : 9 = 967 393 769
1 206 453 879 : 9 = 134 050 431
4 059 721 386 : 9 = 451 080 154
Таких 10-тизначных чисел с неповторяющимися цифрами более трёх миллионов: 9/10*10!=3 265 920
Слайд 23Примеры палиндромов
В русском языке:
Утречко летело к черту
Я ем змея
Я нем и
нежен, не жени меня
Я ужру буржуя!
Нам рак влетел в карман
Цени в себе свинец
Я ужру буржуя!
Нам рак влетел в карман
Цени в себе свинец
Слайд 24Примеры палиндромов
Магический квадрат
Древнейший из сохранившихся палиндромов написан на латыни и датируется
4 в. н.э.
Это фраза "Sator Arepo tenet opera rotas", что означает "Сеятель Арепо с трудом держит колёса".
Слайд 25Примеры палиндромов
В биологии:
Палиндромы в ДНК
1 - палиндром
В химии:
НООССООН – формула щавелевой кислоты
Слайд 27Заключение
Я познакомилась с удивительными натуральными числами - палиндронами. Все они обязаны
своими свойствами простым числам.
Значит, я подтвердила гипотезу о том, что простые числа – это часть чисел, из которых состоят все натуральные числа.
В своей работе я рассмотрела формулы – палиндромы для суммы и разности, произведения и частного двузначных чисел и смогла их доказать, и показать их применение на практике.
Значит, я подтвердила гипотезу о том, что простые числа – это часть чисел, из которых состоят все натуральные числа.
В своей работе я рассмотрела формулы – палиндромы для суммы и разности, произведения и частного двузначных чисел и смогла их доказать, и показать их применение на практике.
Слайд 28
Всем спасибо за внимание!
1 x 1 = 1
11 x 11 =
121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111 = 12345678987654321
Числовой палиндром из единиц
Это интересно - Красота математики
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111 = 12345678987654321
Числовой палиндром из единиц
Это интересно - Красота математики