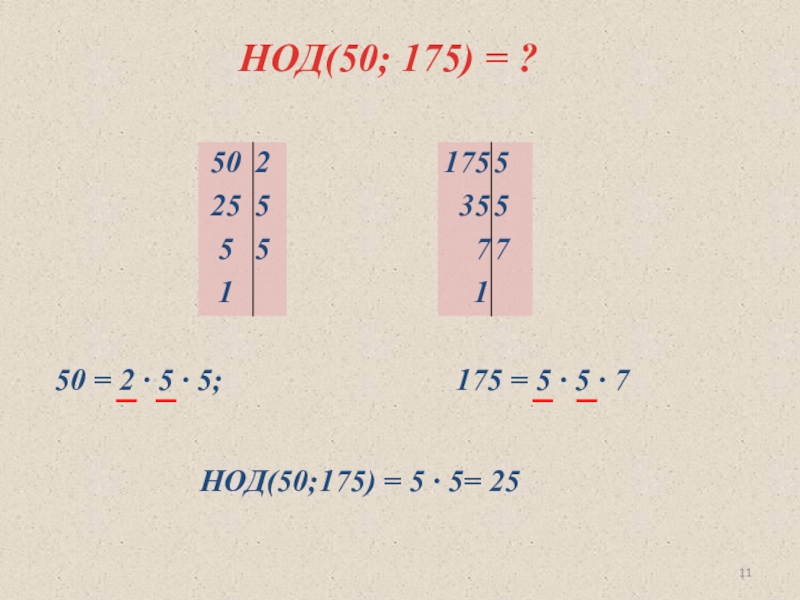Презентация, доклад по математике на тему Нод. Взаимнопростые числа (5 класс)

отрабатывать умение решать задачи на использование НОД чисел;
обобщить имеющиеся у учащихся знания о наибольшем общем делителе натуральных чисел, о взаимно простых числах.

= 6
84 : т = 7; т = 12
84 : е = 21; е = 4
84 : л = 4; л = 21
84 : ь = 3; ь = 28
84 : д = 28; д = 3
84 : е = 6; е = 14
84 : и = 12; и = 7

Расположите ответы в порядке возрастания.

Назовите, какое слово получилось. Дайте определение делителя натурального числа.

без остатка.

числа. Как его найти?

875 = 53 ∙ 7

875 : 5 = 175

Чтобы найти наибольший делитель, надо число разделить на наименьший делитель, отличный от единицы.

11

Назовите наибольший делитель, отличный от самого числа. Как его найти?

Чтобы найти наибольший делитель, надо число разделить на наименьший делитель, отличный от единицы.

2376 : 2 = 1188

наибольший делитель, отличный от самого числа. Как его найти?

Чтобы найти наибольший делитель, надо число разделить на наименьший делитель, отличный от единицы.

5625 : 3 = 1875

и 20; 14 и 35; 48 и 36;
Найдите все делители каждого числа.
Подчеркните их общие делители.

18: 1, 2, 3, 6, 9,18.
9: 1, 3, 9.

10: 1, 10.
7: 1, 7.

15: 1, 3, 5, 15.
20: 1, 2, 4, 5, 10, 20.

14: 1, 2, 7, 14.
35: 1, 5, 7, 35.

48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
36: 1, 2, 3, 4, 6, 9,12, 18, 36.

Выделите их наибольший общий делитель.

чисел, невелико (способ 1).

Обозначают: НОД (48; 36) = 12

Запишем НОД для чисел

НОД (18; 9) = 9,

НОД (10; 7) = 1,

НОД (15; 20) = 5,

НОД (14; 35) = 7,

НОД (48; 36) = 12.

Найдите произведение полученных простых множителей.

НОД(24;60) = 2 ∙ 2 ∙ 3 = 12.

24 = 2 ∙ 2 ∙ 2 ∙ 3; 60 = 2 ∙ 2 ∙ 3 ∙ 5

175 = 5 ∙ 5 ∙ 7

НОД(50;175) = 5 ∙ 5= 25

· 5 · 5; 875 = 5 · 5 ∙ 5 ∙ 7

НОД(675;875) = 5 ∙ 5= 25

· 11 = 198

7920 = 2 ∙ 2 ∙ 2 · 2 · 3 · 3 · 5 · 11
594 = 2 · 3 ∙ 3 ∙ 3 · 11

нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) из множителей, входящих в каждое разложение подчеркнуть общие множители;
3) найти произведение подчеркнутых множителей.

Если все данные числа делятся на одно из них, то это число и является наибольшим общим делителем данных чисел.

(32; 40) = 8.
Ответ: 8 наборов.

В одной корзине 32 яблока, в другой корзине 40 груш. Какое наибольшее количество одинаковых наборов можно составить, используя эти фрукты.

Найти наибольшее число, на которое делятся числа 32 и 40, то есть найти их наибольший общий делитель.

8, 11, 22, 44, 88

Для каждой пары чисел: 35 и 88; 25 и 9; 5 и 3; 7 и 8;
Найдите все делители каждого числа.
Подчеркните их общие делители.

НОД (35; 88) = 1.

НОД (25; 9) = 1;

НОД( 5; 3) = 1;

НОД (7; 8) = 1.

Выделите их наибольший общий делитель.

25: 1, 5, 25 9: 1, 3, 9

5: 1, 5 3: 1, 3

7: 1, 7 8: 1, 8

3) = 1

НОД (7; 8) = 1

Такие числа называются
взаимно простыми.

Натуральные числа называют взаимно простыми, если их наибольший общий делитель
равен 1.

натуральных чисел без разложения на множители. Он носил название «Алгоритма Евклида».
Он заключается в том, что наибольшим общим делителем двух натуральных чисел является последний, отличный от нуля, остаток при последовательном делении чисел.

Историческая минутка.

Положим, требуется найти НОД (455; 312), Тогда
455 : 312 = 1 (ост. 143), получаем 455 = 312 ∙ 1 + 143
312 : 143 = 2 (ост. 26), 312 = 143 ∙ 2 + 26
143 : 26 = 5 (ост. 13), 143 =26 ∙ 5 + 13
26: 13 = 2 (ост. 0), 26 = 13 ∙ 2
Последний делитель или последний, отличный от нуля остаток 13 будет искомым НОД (455; 312) = 13.

одинаковые подарки. Во всех подарках вместе было 123 апельсина и 82 яблока. Сколько ребят присутствовало на елке? Сколько апельсинов и сколько яблок было в каждом подарке?

Найти НОД чисел 123 и 82.

Количество апельсинов и яблок должно делиться на одно и то же наибольшее число.

НОД (123; 82) = 41, значит, 41 человек.
123 : 41 = 3 (ап.)
82 : 41 = 2 (ябл.)
Ответ: ребят 41, апельсинов 3, яблок 2.

Сколько ребят -?
Сколько яблок - ?
Сколько апельсинов -?

= 10

НОД (8; 24) = 8

НОД (15; 35) = 5

НОД(13; 26) = 13

НОД (8; 9) = 1

НОД (24; 60) = 12

значит, 53 пассажира в
одном автобусе.

424 : 53 = 8 (авт.) - в лес.

477 : 53 = 9 (авт.) - на озеро.

8 + 9 = 17 (авт.)

Ответ: 17 автобусов, 53 пассажира в каждом.

Для поездки за город работникам завода было выделено несколько автобусов, с одинаковым числом мест в каждом автобусе. 424 человека поехали в лес, а 477 человек - на озеро. Все места в автобусах были заняты, и ни одного человека не осталось без места. Сколько автобусов было выделено и сколько пассажиров было в каждом автобусе?

называют наибольшим общим делителем двух натуральных чисел?
Какие числа называют взаимно простыми?
Как найти наибольший общий делитель нескольких натуральных чисел?
Если числа взаимно простые, то какому числу равен их наибольший общий делитель?
Верно ли: «Если числа простые, то они взаимно простые»? Ответ обоснуйте.