- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Красота привлекает , исповедование увлекает
Содержание
- 1. Презентация по математике на тему Красота привлекает , исповедование увлекает
- 2. Учитель математики: Серикбаева О.Ж.Решение уравнений и неравенств с модулем
- 3. Актуальность выбранной темыПрактически каждый учитель знает, какие
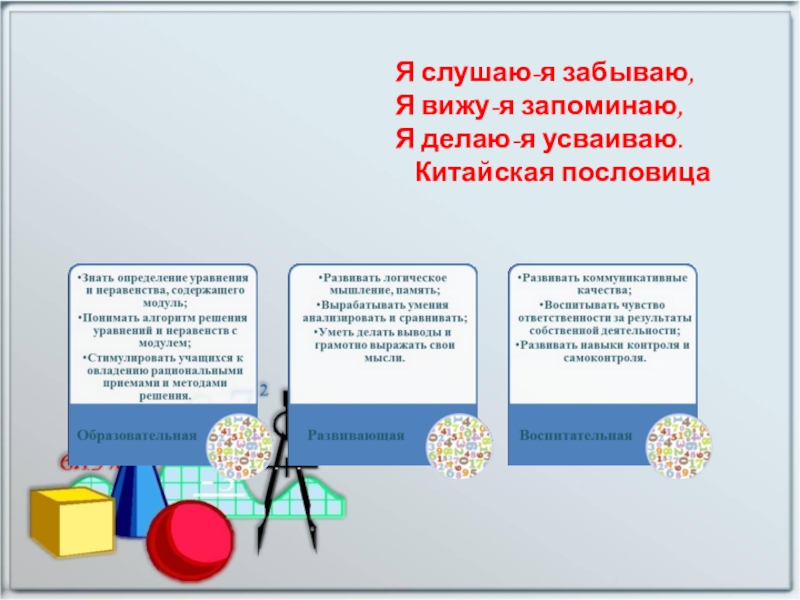
- 4. Я слушаю-я забываю,Я вижу-я запоминаю,Я делаю-я усваиваю.Китайская пословицаЦели:
- 5. Формы урока: комбинированный урок, интегрированный урок ,урок-
- 6. 6 КЛАСС-2
- 7. 2) Модулем числа называют расстояние в единичных
- 8. x2-2|x|=0Решение одного уравнения несколькими методами: Метод разложения
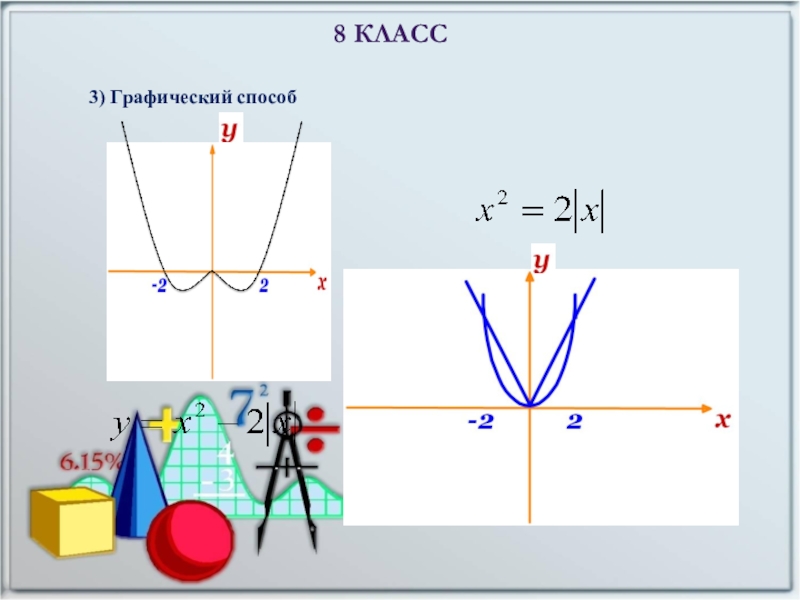
- 9. 3) Графический способ8 КЛАСС
- 10. ТЕСТОВЫЕ ЗАДАНИЯ по теме «Решение уравнений с
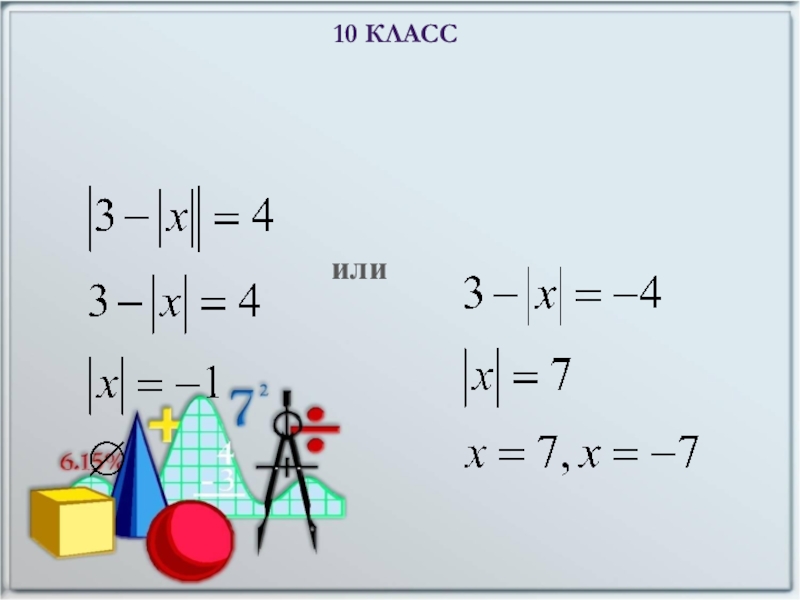
- 11. 10 КЛАССРешение уравнений со сложным модулемили
- 12. Ответ: 3, -3, 1, -110 КЛАСС
- 13. ЗАДАНИЕ С СОПУТСТВУЮЩИМИ УКАЗАНИЯМИ И ИНСТРУКЦИЯМИ
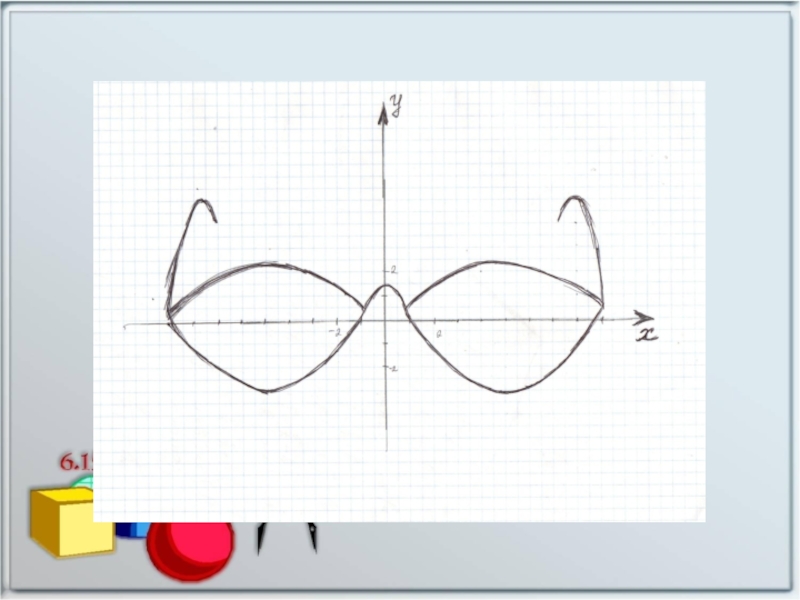
- 14. Рисуем графиками функций
- 15. Слайд 15
- 16. Основные приемы и методы решения логических задач
- 17. Путешествие в математику План путешествия:1. Развиваем гибкость
- 18. 7 класс. У двух зрячих
- 19. II этап. Ситуации в жизни такие: либо
- 20. IIIэтап. Без логики нет математики7 класс.
- 21. IV этап. В технологию тропинки одолеем
- 22. V этап. Точка соприкосновения: “Где же
- 23. VI этап. И фокусы покажем,
- 24. Лента МёбиусаИнтересные метаморфозы таит
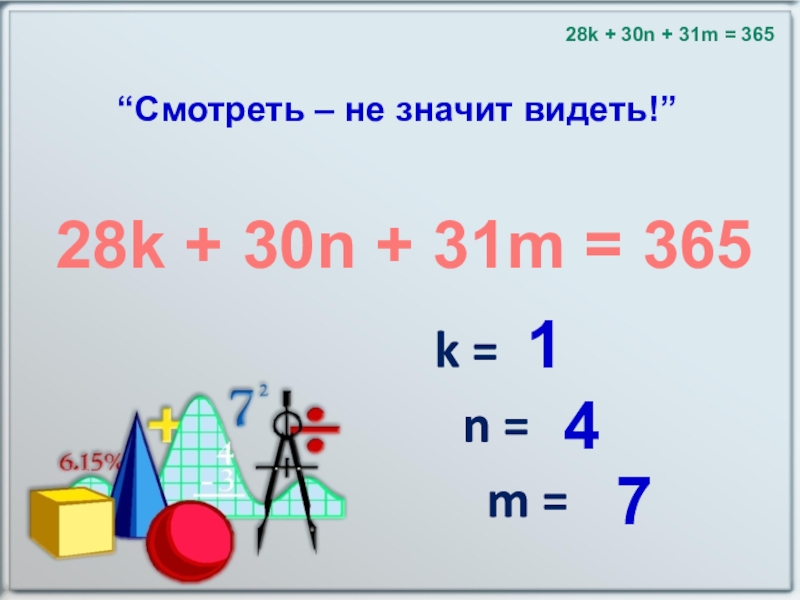
- 25. “Смотреть – не значит видеть!” k
- 26. 28k + 30n + 31m = 365Тетраэдр
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Спасибо за внимание!
Слайд 1Мастер – класс
«Красота привлекает,
исследование увлекает»
Предмет математики настолько серьезен, что нельзя
Слайд 3Актуальность выбранной темы
Практически каждый учитель знает, какие проблемы вызывают у учащихся
Выбор темы обусловлен тем, что, во-первых задачи, связанные с абсолютными величинами часто встречаются на математических олимпиадах и экзаменах, это понятие широко применяется не только в школьном курсе математики, но и в высшей. Так в математическом анализе понятие абсолютной величины числа используется при определении основных понятий, предела , ограниченности функции и др. в теории приближенных вычислении употребляется понятие абсолютной погрешност.
Слайд 5Формы урока: комбинированный урок, интегрированный урок ,урок- игра , урок –практикум,
Методы и приемы: проблемный, частично-поисковый, дифференцированный.
Технологии: личностно-ориентированное обучение
Средства обучения: компьютерная презентация, флипчарт
Оборудование: мультимедийный проектор, интерактивная доска, персональные компьютеры, карточки – задания, лист-рефлексии.
Слайд 72) Модулем числа называют расстояние в единичных отрезках от начала отчета
6 КЛАСС
Графический диктант
ДА _ НЕТ Λ
Слайд 8x2-2|x|=0
Решение одного уравнения несколькими методами:
Метод разложения на множители
|x|=x, x≥0
x2-2x=0
x(x-2)=0 x(x+2)=0
x=0, x=2 x=0, x=-2
2) Метод введения новой переменной
Пусть |x|=t, тогда уравнение примет вид:
t2-2t=0
t=0, t=2
|x|=0 |x|=2
x=0 x=-2, x=2
8 КЛАСС
Слайд 10ТЕСТОВЫЕ ЗАДАНИЯ по теме «Решение уравнений с модулем». 1. Какие числа
2. Решите уравнение |х+3|=7: а) 7; б) -4; в) 10; -4; г) 4; -10.
3. Определите координаты точки пересечения графиков функций у=|2х+1| и у=0: а) (0;0); б) (-0,5;0); в) (0;-0,5); г) (0,5;0).
4. Решите уравнение |х+3|+|х-1|=6: а) 3; -2; б) 4; -2; в) -4; 2; г) 2; -3.
5. Сколько точек пересечения имеют графики функций у=||5,5х-4|+2| и у=3? а) 1; б) 2; в) 3; г) 4.
6. Решите уравнение |3х-7|=1-х: а) 2; 3; б) -2; 3; в) -3; 2; г) -2; -3.
7. Сколько решений имеет уравнение (2,5х-5)2=(0,5х-6)2: а) 1; б) 2; в) 3; г) 4.
Слайд 13ЗАДАНИЕ С СОПУТСТВУЮЩИМИ УКАЗАНИЯМИ И ИНСТРУКЦИЯМИ
Решить уравнение |х-2|+|2х-7|=3.
Решение.
Решим
Слайд 16Основные приемы и методы решения логических задач
Теория, мой друг, суха,
зеленеет жизни древо.
И.В.Гете
Известно несколько различных способов решения логических задач:
Метод рассуждений;
Метод таблиц;
Метод графов;
Метод блок-схем;
Метод бильярда;
Метод кругов Эйлера.
Слайд 17Путешествие в математику
План путешествия:
1. Развиваем гибкость ума через решение задач.
2.
3. Без логики нет математики.
4. Точка соприкосновения: “Где же зарыта кошка?”
5. И фокусы покажем,
и секрет расскажем.
28k + 30n + 31m = 365
Слайд 18
7 класс.
У двух зрячих один брат слепой, но
зрячих братьев. Как это может быть?
11 класс.
Известно, что бумеранг можно бросить
так, что он вернется обратно.
А можно как-то ухитриться
и бросить теннисный мяч так,
чтобы он вернулся обратно?
I этап. Развиваем гибкость ума через решение задач.
28k + 30n + 31m = 365
Слайд 19II этап. Ситуации в жизни такие: либо сложные, либо простые
7 класс.
Трём приятелям вручили четыре яблока. Как, не разрезая и не выбрасывая яблок, разделить их между приятелями так, чтобы каждый получил не больше остальных?
11класс
Какое из чисел больше:
3111 или 1714?
28k + 30n + 31m = 365
Слайд 20IIIэтап. Без логики нет математики
7 класс.
В трех мешках
11 класс.
Лошадь съедает воз сена за месяц,
коза — за два месяца, овца —
за три месяца.
За какое время лошадь, коза и
овца вместе съедят такой же
воз сена?
28k + 30n + 31m = 365
Слайд 21
IV этап. В технологию тропинки одолеем без запинки.
7класс
В
11класс
В кафе имеются три первых блюда,
пять вторых и два третьих. Сколькими
способами посетитель кафе может
выбрать обед, состоящий из первого,
второго и третьего блюд?
28k + 30n + 31m = 365
Слайд 22
V этап. Точка соприкосновения: “Где же зарыта кошка?”
7класс
Найти величину угла
биссектрисами смежных и
вертикальных углов.
11класс
Представьте себе, что вы охватили
земной шар по экватору. А теперь
прибавьте к длине окружности 1 метр
и снова охватите земной шар,
у вас должен получиться зазор.
Пролезет ли кошка через этот зазор?
28k + 30n + 31m = 365
Слайд 23
VI этап. И фокусы покажем, и секрет расскажем!
Вопрос:
без чего невозможно
сделать табуретку,
даже если есть
все-все инструменты
и все-все деревяшки,
гвозди, клей?
28k + 30n + 31m = 365
Слайд 24 Лента Мёбиуса
Интересные метаморфозы таит в себе лента Мебиуса,
Что произойдет, если разрезать по центральной линии ленту Мебиуса?
Сколько она имеет поверхностей: одну или две? Догадливый муравей проверит.
А если красить по поверхности, то лента закрасится с одной стороны или с двух?
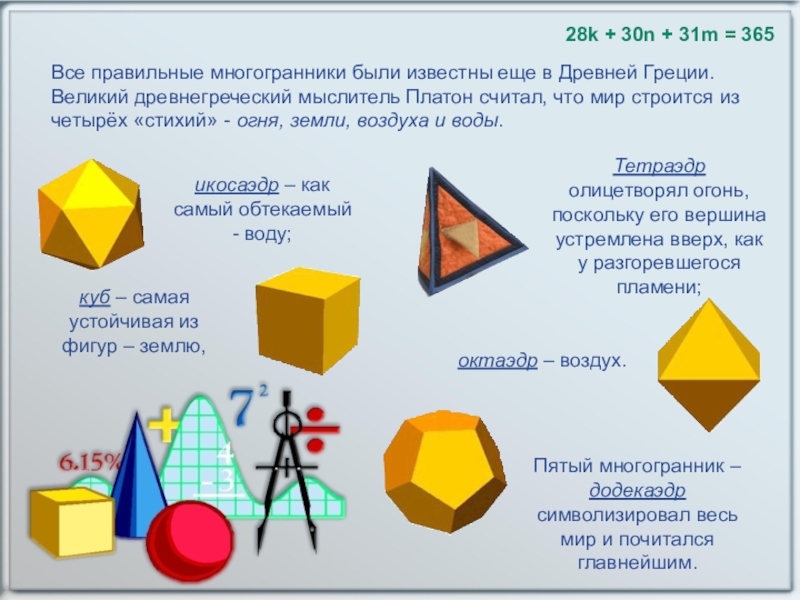
Слайд 2628k + 30n + 31m = 365
Тетраэдр олицетворял огонь, поскольку его
икосаэдр – как самый обтекаемый - воду;
куб – самая устойчивая из фигур – землю,
октаэдр – воздух.
Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.
Все правильные многогранники были известны еще в Древней Греции. Великий древнегреческий мыслитель Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды.