- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Конус
Содержание
- 1. Презентация по математике на тему Конус
- 2. Конус в переводе с греческого «konos» означает
- 3. Много сделала для геометрии школа Платона (428-348
- 4. Конусы вокруг нас
- 5. Карликовое дерево
- 6. Конусообразные дома - трулли
- 7. Мороженное
- 8. Оградительные конусы
- 9. Туфовые дома (высечены в скале)
- 10. Кусты в королевском саду
- 11. Конусы - ракушки
- 12. Крыша-конус
- 13. Надувные конусы
- 14. КонусКонусом называется тело, которое состоит из круга
- 15. А ОВКонус- это геометрическое тело, образованное вращением прямоугольного треугольника вокруг одного из его катетов.
- 16. Элементы конусаОСНОВАНИЕВЕРШИНАВЫСОТА H, ось вращения R РАДИУСОБРАЗУЮЩАЯ LLH
- 17. Выпишите элементы конуса.Ось вращения-АООбразующие-АВ, АD, АЕ, АСВысота- АОРадиусы- ОВ, ОС, ОDДиаметр- ВСВершина- АОснование- круг.ВDСЕОА
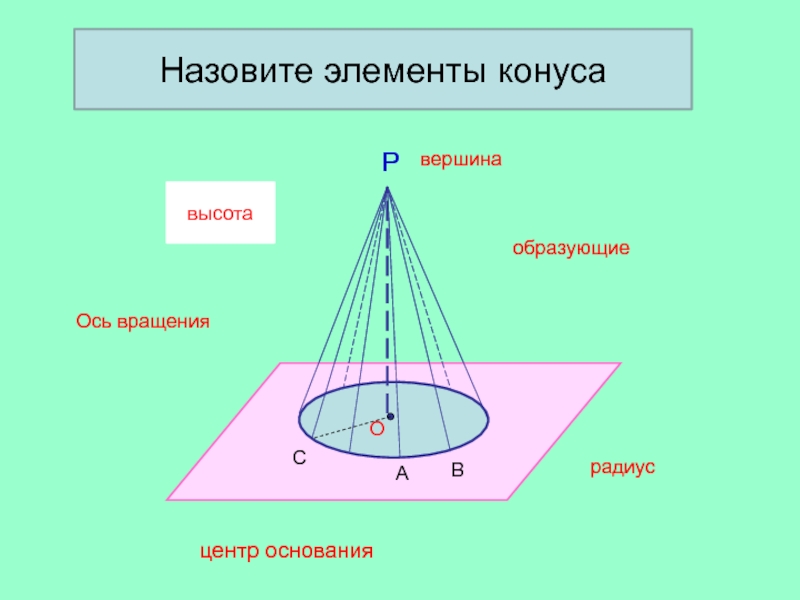
- 18. Рвершина образующиерадиусОцентр основанияВАСвысотаНазовите элементы конусаОсь вращения
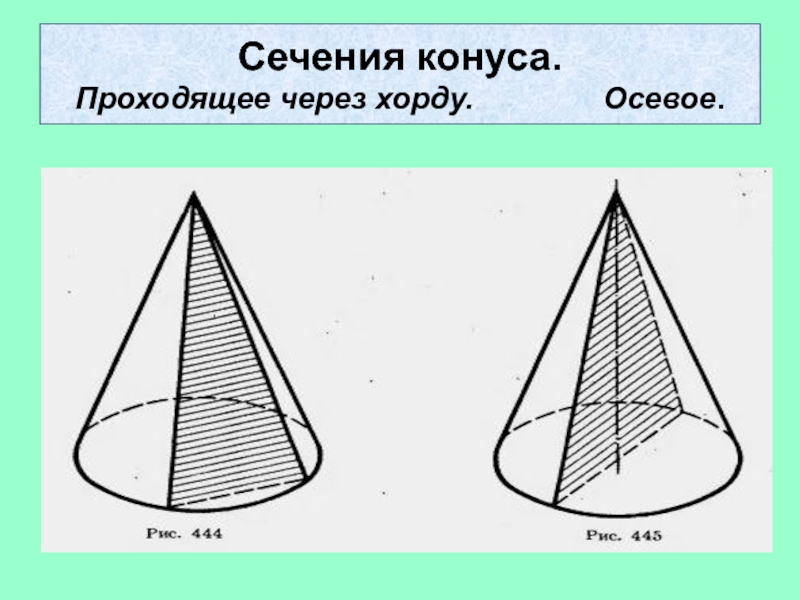
- 19. Сечения конуса. Проходящее через хорду. Осевое.
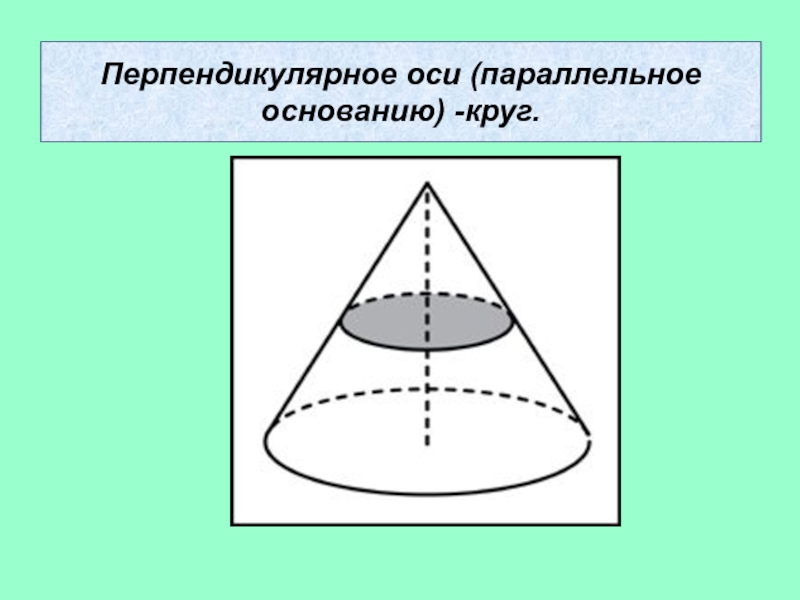
- 20. Перпендикулярное оси (параллельное основанию) -круг.
- 21. Усеченным конусом называется часть конуса, ограниченная его
- 22. Применение конуса и усеченного конуса в повседневной жизни
- 23. Применение конуса и усеченного конуса в повседневной жизни
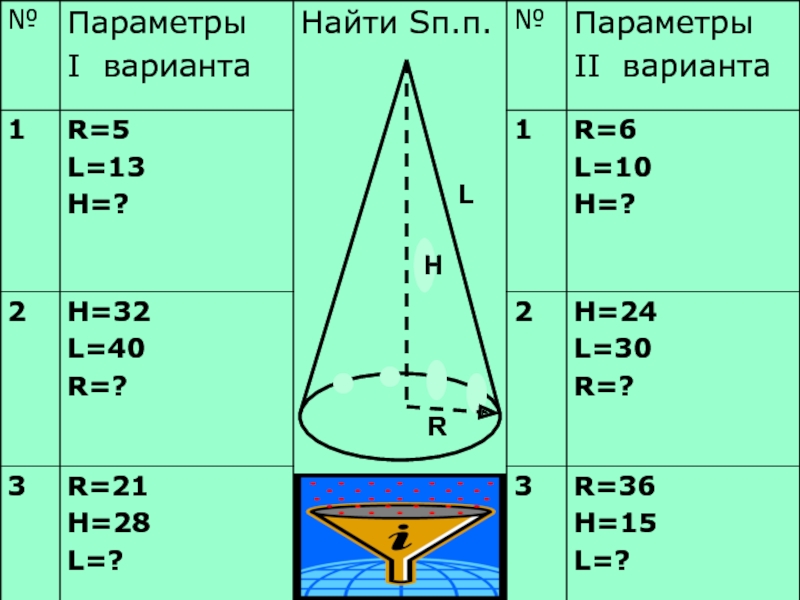
- 24. Площадь полной поверхности конуса
- 25. Боковая поверхность конусаЕсли разрезать конус по образующей,
- 26. Полная поверхность конуса Зная формулу боковой поверхности конуса выведем формулу нахождения полной поверхности конусаRSполн=Sбок+SоснSбок=πRLSосн=πR2Sполн=πRL+πR2Sполн=πR(L+R)
- 27. Площадь боковой поверхности усечённого конусаПлощадь боковой поверхности
- 28. Задача : Конусообразная палатка высотой 4 м
- 29. RLH
- 30. ЗадачиЗадача 1. Образующая конуса равна 18 см
- 31. ЗадачиЗадача 4. Радиусы оснований усеченного конуса 12
- 32. Объем конусаРассмотрим пирамиду вписанную в конусВспомним формулу
- 33. Задача: Стог сена имеет форму цилиндра с
- 34. ОБЪЁМ УСЕЧЁННОГО КОНУСАОбъем v усечённого конуса, высота
Конус в переводе с греческого «konos» означает «сосновая шишка». С конусом люди знакомы с глубокой древности. В 1906 году была обнаружена книга Архимеда (287-212 гг. до н.э.) «О методе», в которой дается решение задачи об объеме
Слайд 2Конус в переводе с греческого «konos» означает «сосновая шишка». С конусом
люди знакомы с глубокой древности. В 1906 году была обнаружена книга Архимеда (287-212 гг. до н.э.) «О методе», в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа Демокриту (470-380 гг. до н.э.) – древнегреческому философу-материалисту. С помощью этого принципа Демокрит получил формулу для вычисления объема пирамиды и конуса.
Слайд 3 Много сделала для геометрии школа Платона (428-348 гг. до н.э.). Платон
был учеником Сократа (470-399 гг. до н.э.). Он в 387 г. до н.э. основал в Африке Академию, в которой работал 20 лет. Каждый, входящий в Академию, читал надпись: «Пусть сюда не входит никто, не знающий геометрии». Школе Платона, в частности, принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.
Большой трактат о конических сечениях был написан Аполлонием Пергским (260-170 гг. до н.э.) – учеником Евклида (III в. До н.э.), который создал великий труд из 15 книг под названием «Начала». Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.
Большой трактат о конических сечениях был написан Аполлонием Пергским (260-170 гг. до н.э.) – учеником Евклида (III в. До н.э.), который создал великий труд из 15 книг под названием «Начала». Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.
Слайд 14Конус
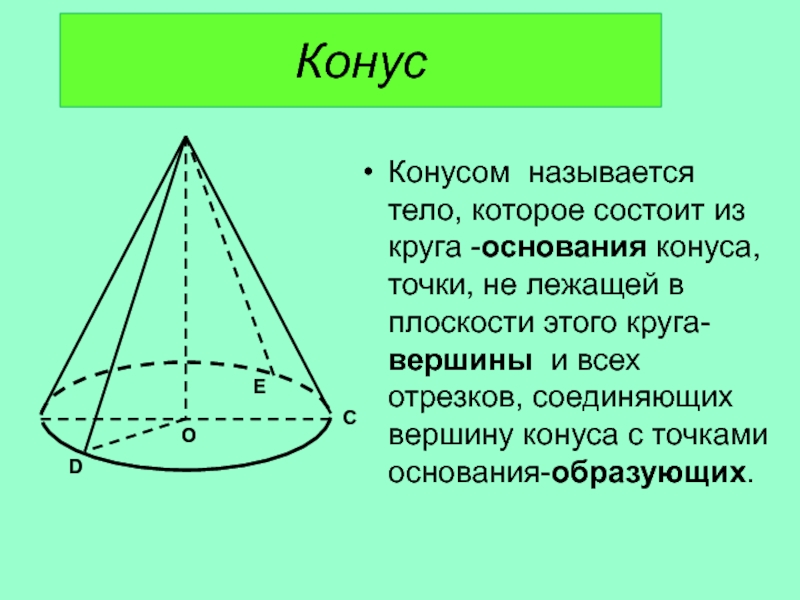
Конусом называется тело, которое состоит из круга -основания конуса, точки, не
лежащей в плоскости этого круга- вершины и всех отрезков, соединяющих вершину конуса с точками основания-образующих.
D
С
Е
О
Слайд 15А
О
В
Конус- это геометрическое тело, образованное вращением прямоугольного треугольника вокруг одного
из его катетов.
Слайд 17Выпишите элементы конуса.
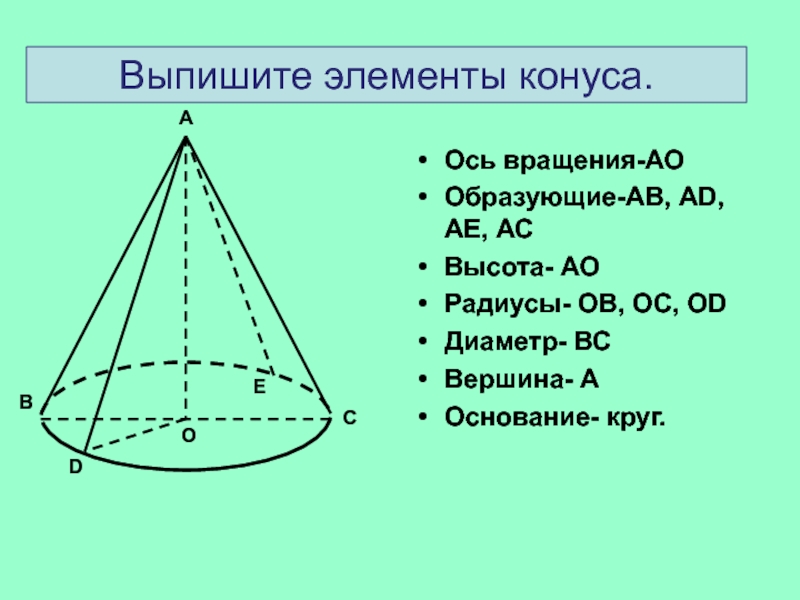
Ось вращения-АО
Образующие-АВ, АD, АЕ, АС
Высота- АО
Радиусы- ОВ, ОС, ОD
Диаметр-
ВС
Вершина- А
Основание- круг.
Вершина- А
Основание- круг.
В
D
С
Е
О
А
Слайд 21Усеченным конусом называется часть конуса, ограниченная его основанием и сечением, плоскость
которого параллельна плоскости основания.
Виды конусов
Тело, образованное вращением прямоугольной трапеции вокруг боковой стороны, являющейся высотой трапеции.
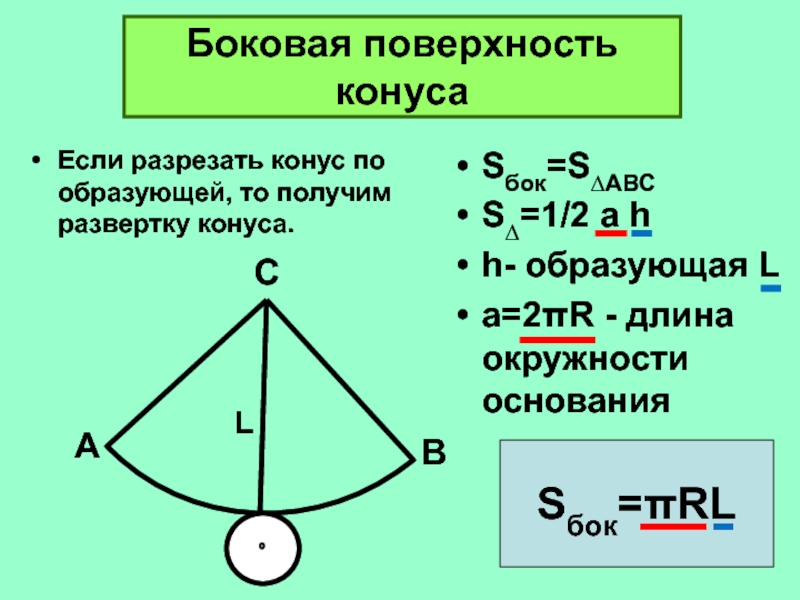
Слайд 25Боковая поверхность конуса
Если разрезать конус по образующей, то получим развертку конуса.
Sбок=S∆АВС
S∆=1/2
a h
h- образующая L
a=2πR - длина окружности основания
h- образующая L
a=2πR - длина окружности основания
L
A
B
C
Sбок=πRL
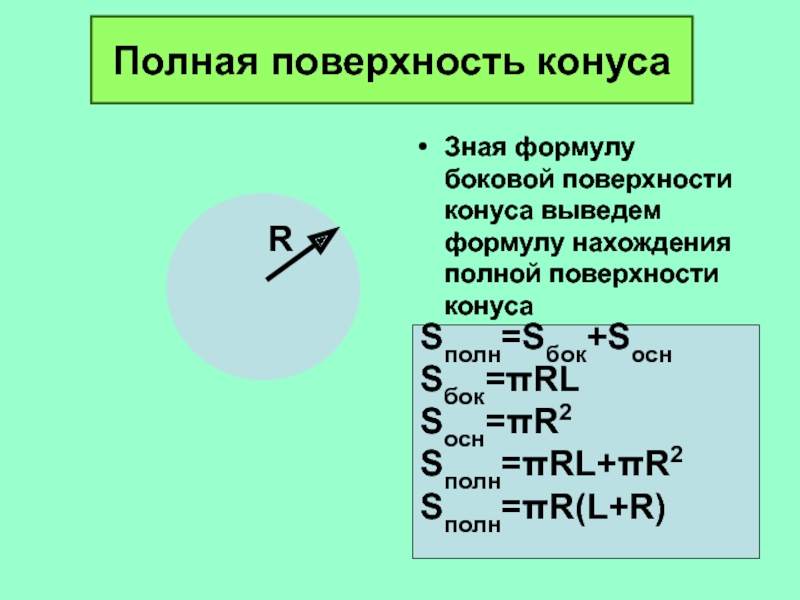
Слайд 26Полная поверхность конуса
Зная формулу боковой поверхности конуса выведем формулу нахождения
полной поверхности конуса
R
Sполн=Sбок+Sосн
Sбок=πRL
Sосн=πR2
Sполн=πRL+πR2
Sполн=πR(L+R)
Слайд 27Площадь боковой поверхности усечённого конуса
Площадь боковой поверхности усечённого конуса равна произведению
полусуммы длин окружностей оснований на образующую.
Sбок= П(r+r1)L
Sбок= П(r+r1)L
Слайд 28Задача : Конусообразная палатка высотой 4 м с диаметром основания 6
м покрыта сверху парусиной. Сколько квадратных метров парусины пошло на палатку?
Слайд 30Задачи
Задача 1. Образующая конуса равна 18 см и наклонена к плоскости
основания под углом 60°. Найдите площадь полной поверхности конуса.
Задача 2. Через вершину конуса и хорду АВ основания конуса, равную 16 см, проведено сечение, образующее с плоскостью основания угол 60°. Радиус основания конуса равен 10 см. Найдите площадь полной поверхности конуса.
Задача 3. Треугольник АВС со сторонами АВ = 41 см, АС = 15 см и ВС = 52 см вращается вокруг прямой, содержащей его большую сторону. Найдите площадь полной поверхности тела вращения.
Задача 2. Через вершину конуса и хорду АВ основания конуса, равную 16 см, проведено сечение, образующее с плоскостью основания угол 60°. Радиус основания конуса равен 10 см. Найдите площадь полной поверхности конуса.
Задача 3. Треугольник АВС со сторонами АВ = 41 см, АС = 15 см и ВС = 52 см вращается вокруг прямой, содержащей его большую сторону. Найдите площадь полной поверхности тела вращения.
Слайд 31Задачи
Задача 4. Радиусы оснований усеченного конуса 12 см и 6 см,
высота его равна 8 см. Найдите площадь боковой и полной поверхности усеченного конуса.
Задача 5. Радиусы оснований усеченного конуса равны 3 см и 6 см, а высота равна 4 см. Найдите площадь осевого сечения и боковой поверхности усеченного конуса.
Задача 6. Тело получено при вращении ромба со стороной 18 см и углом 60° вокруг стороны. Найдите площадь полной поверхности тела вращения.
Задача 5. Радиусы оснований усеченного конуса равны 3 см и 6 см, а высота равна 4 см. Найдите площадь осевого сечения и боковой поверхности усеченного конуса.
Задача 6. Тело получено при вращении ромба со стороной 18 см и углом 60° вокруг стороны. Найдите площадь полной поверхности тела вращения.
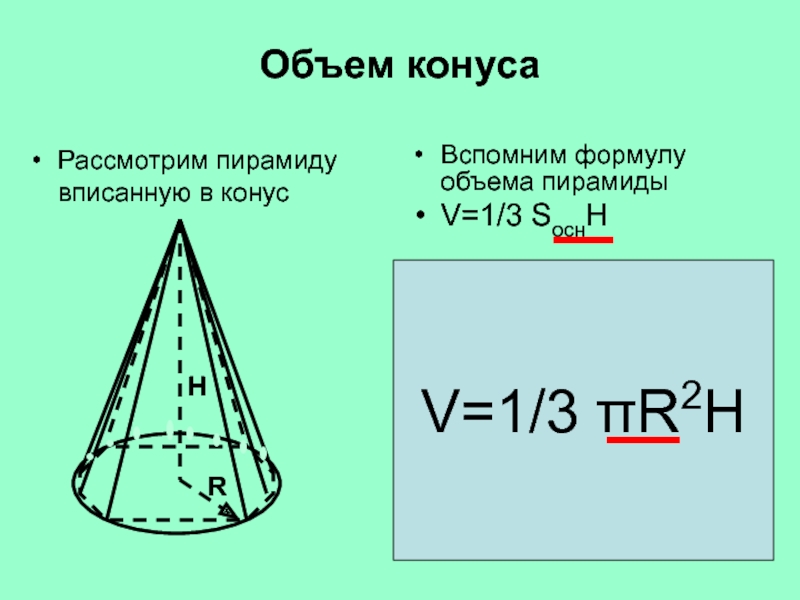
Слайд 32Объем конуса
Рассмотрим пирамиду вписанную в конус
Вспомним формулу объема пирамиды
V=1/3 SоснН
Чем больше
сторон у основания пирамиды тем больше пирамида стремится к конусу, а площадь основания к площади круга.
Выведите самостоятельно формулу объема конуса
Выведите самостоятельно формулу объема конуса
Н
V=1/3 πR2Н
R
Слайд 33Задача: Стог сена имеет форму цилиндра с коническим верхом. Радиус его
основания равен 2,5м, высота 4м, причем цилиндрическая часть стога имеет высоту 2,2м. Плотность сена 0,03г/см3. Определите массу стога сена.
Слайд 34ОБЪЁМ УСЕЧЁННОГО КОНУСА
Объем v усечённого конуса, высота которого равна h, а
площади оснований равны s и s1, вычисляется по формуле
V =1/3пh(R2+r2+Rr)
V =1/3пh(R2+r2+Rr)