- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Комбинаторные конструкции
Содержание
- 1. Презентация по математике на тему Комбинаторные конструкции
- 2. В комбинаторике чаще всего используются следующие построения
- 3. Задача 1. Подсчитать количество слов длины k
- 4. 2. Размещение.Рассмотрим некоторое множество объектов. Приготовим ряд
- 5. В отличии от задачи 1, где букву
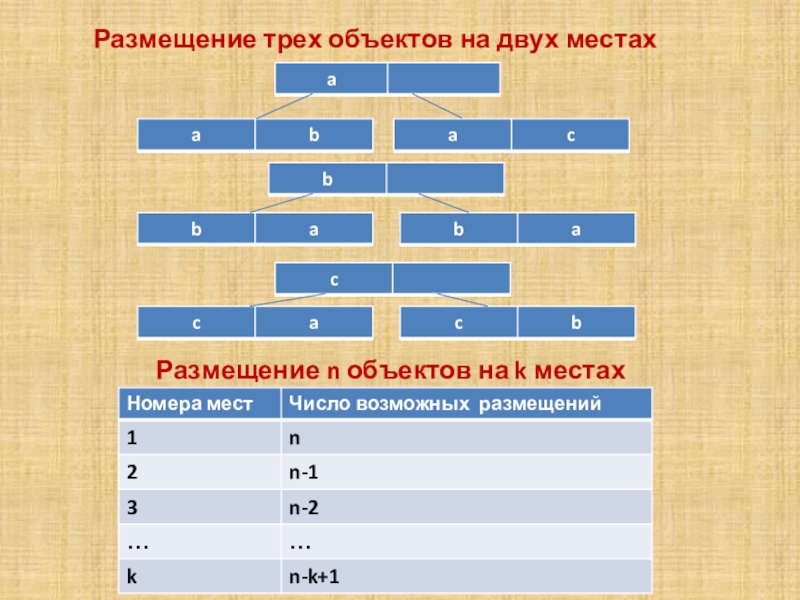
- 6. Размещение трех объектов на двух местахРазмещение n объектов на k местах
- 7. Всего вариантов: n(n-1)(n-2)…(n-k+1)Число размещений n объектов на
- 8. 3. Перестановка.Рассмотрим множество, содержащее n объектов. Мы
- 9. Дерево перестановок
- 10. Главный принцип при решении комбинаторных задач –
- 11. 2. Тесты с выбором ответа. Человеку предложили
- 12. 3. Слова с различными буквами. В алфавите
- 13. ПерестановкаРазмещение
Слайд 2В комбинаторике чаще всего используются следующие построения (конструкции):
Построение слов.
Рассмотрим некоторое
Слово – это последовательность букв данного алфавита.
Длина слова – число букв в данном слове.
Например, алфавит Азбуки Морзе состоит из двух символов : точка • и тире −.
Построение слов:
Слово длины 1 Слово длины 2 Слово длины 3
Каждая буква алфавита может быть использована один раз, несколько раз или ни разу
Слайд 3Задача 1. Подсчитать количество слов длины k в алфавите из n
В слове длины k имеется k мест. На первое ставим любую из n букв. При заполнении очередного места число возможностей увеличивается в n раз.
Ответ:
Число слов длины k в алфавите из n букв равно
Пример. Двухбуквенные слова в алфавите из трех букв
Слайд 42. Размещение.
Рассмотрим некоторое множество объектов. Приготовим ряд из пустых мест. Мы
Ряд, заполненный объектами данного множества, называют размещением. Пусть число объектов в множестве равно n, а длина ряда (число мест в нем) равна k.
Слайд 5В отличии от задачи 1, где букву можно использовать не один
На первое место ставим любой из n объектов. На каждом следующем шаге число возможностей уменьшается на единицу.
Ответ:
Задача 2. Подсчитать число размещений n объектов на k местах.
Обратите внимание, что последний множитель равен n-(k-1)=n-k+1. Заметим, что если k>n, то один из множителей будет равен нулю, поскольку нельзя n объектами занять число мест, большее, чем n.
Слайд 7Всего вариантов: n(n-1)(n-2)…(n-k+1)
Число размещений n объектов на k местах равно произведению
Слайд 83. Перестановка.
Рассмотрим множество, содержащее n объектов. Мы хотим расставить их по
Задача 3. Подсчитать число перестановок n объектов.
Ясно, что эта задача совпадает с задачей о размещениях в том случае, когда число объектов совпадает с числом мест – мы расставляем все n объектов, используя n имеющихся мест. Аналогично задаче 2 получаем ответ
Так как число множителей равно n, то последним будет число 1. Удобно переставить множители и записать результат в виде произведения всех натуральных чисел от 1 до n:
Слайд 10Главный принцип при решении комбинаторных задач – не пытаться применять готовую
Двоичные ответы. Человеку задают 10 вопросов. На каждый из них он отвечает «да» или «нет». Сколько имеется различных вариантов ответов на все 10 вопросов?
Для ответа на первый вопрос есть 2 варианта. Если уже построены ответы на несколько вопросов, то ответ на следующий удвоит число вариантов.
Ответ: . Разумеется в этой задаче встретилась конструкция построения слов в алфавите из 2 букв.
Слайд 112. Тесты с выбором ответа. Человеку предложили тест из 6 вопросов.
Для ответа на первый вопрос есть 5 вариантов ответа. При переходе к очередному вопросу число вариантов будет увеличиваться в 5 раз.
Ответ: . Конструкция сохранилась. Изменилось число букв в алфавите – теперь их стало 5.
Слайд 123. Слова с различными буквами. В алфавите 10 букв. Сколько можно
На первое место ставим любую из 10 букв, на второе – любую, кроме той, которая уже взята первой. Получаем 10*9 вариантов. На трете место можно поставить любую из 8 неиспользованных букв.
Ответ: 10*9*8 = 720. Использована конструкция размещений – на тех местах размещали без повторений 10 букв.
4. Анаграммы слова с различными буквами (Анаграмма – слово с переставленными буквами). Сколько существует анаграмм для слова КАТЕР?
Все пять букв этого слова разные. Переставить 5 букв можно 5! способами.
Ответ: