- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Интегральное исчисление
Содержание
- 1. Презентация по математике на тему Интегральное исчисление
- 2. Из истории интегралов
- 3. Евдокс Книдский.
- 4. Г. ЛейбницВ 1675 г. ввел символ
- 5. К. ФурьеВвел обозначение называемое определенным интегралом
- 6. И. Ньютон
- 7. Строгое изложение теории интеграла появилось в XIX
- 8. Своего нынешнего состояния методы интегрирования в основном
- 9. Первообразная.Функция F называется первообразной для функции f
- 10. Площадь криволинейной трапеции
- 11. На отрезке [a; b] оси Ох задана
- 12. ТеоремаЕсли f – непрерывная и неотрицательная на
- 13. ПРИМЕРВычислить площадь фигуры, ограниченной линиями: у =
- 14. Неопределённый интеграл. Неопределённым интегралом выражения называется общий
- 15. Неопределённые интегралы от тригонометрических функций.
- 16. Неопределённые интегралы от некоторых функций. = 2
- 17. Формула Ньютона - ЛейбницаЕсли F – первообразная для f на отрезке [a; b], то
- 18. ПРИМЕРВычислить интегралРешение:
- 19. Спасибо за внимание!
Слайд 1Интегральное исчисление
СОГБПОУ «Вяземский медицинский колледж
имени Е.О. Мухина»
Подготовила преподаватель математики
Лиманская Н.А.
Слайд 3 Евдокс Книдский.
Задачи нахождения квадратур и кубатур.
Слайд 4Г. Лейбниц
В 1675 г. ввел символ -знак интеграла
И.
В 1696 г. – Интегральное
исчисление (calculus integralis).
Слайд 6 И. Ньютон
Независимо друг от друга установили связь операций дифференцирования и интегрирования.
Слайд 8Своего нынешнего состояния методы интегрирования в основном достигли в работах Л.Эйлера.
го и П.Л.Чебышева завершили развитие этих методов.
Слайд 9Первообразная.
Функция F называется первообразной для функции f на заданном промежутке, если
Слайд 11На отрезке [a; b] оси Ох задана непрерывная функция f, не
Слайд 12Теорема
Если f – непрерывная и неотрицательная на отрезке [a; b] функция,
S = F (b) – F (a).
Слайд 13ПРИМЕР
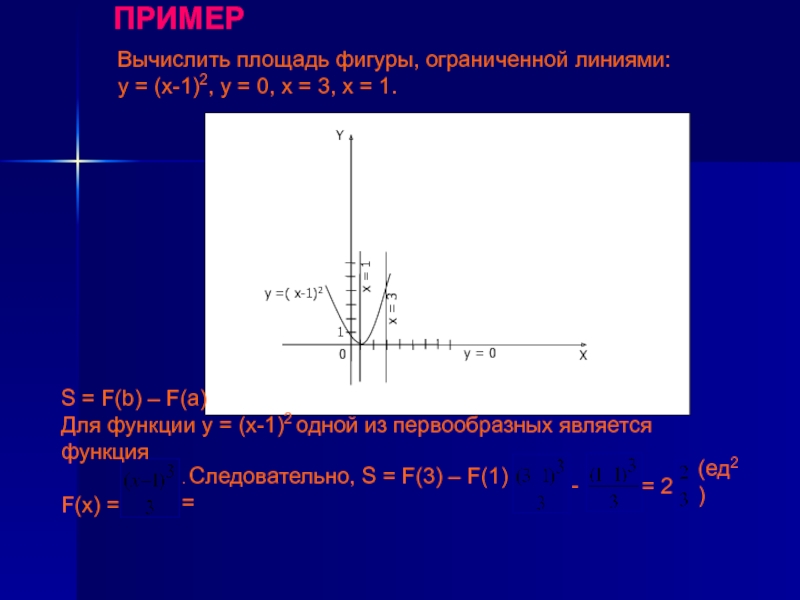
Вычислить площадь фигуры, ограниченной линиями:
у = (х-1)2, у = 0,
y = 0
x = 3
x = 1
y =( x-1)2
S = F(b) – F(a)
Для функции у = (х-1)2 одной из первообразных является функция
F(x) =
. Следовательно, S = F(3) – F(1) =
-
= 2
(ед2)
Слайд 14Неопределённый интеграл.
Неопределённым интегралом выражения
называется общий вид его первообразной функции.
Неопределённый интеграл
Выражение называется подынтегральным выражением.
Функция - подынтегральной функцией ,
переменная x – переменной интегрирования.
Вычисление неопределённого интеграла данной функции называется интегрированием.










![Презентация по математике на тему Интегральное исчисление На отрезке [a; b] оси Ох задана непрерывная функция f, не На отрезке [a; b] оси Ох задана непрерывная функция f, не меняющая на нем знака. Фигуру, ограниченную](/img/thumbs/9ee10ef375c6da8f420bf1da729004b3-800x.jpg)
![Презентация по математике на тему Интегральное исчисление ТеоремаЕсли f – непрерывная и неотрицательная на отрезке [a; b] функция, ТеоремаЕсли f – непрерывная и неотрицательная на отрезке [a; b] функция, а F – ее первообразная на](/img/thumbs/ec6dc8db56dfbe026693eb66adca1091-800x.jpg)



![Презентация по математике на тему Интегральное исчисление Формула Ньютона - ЛейбницаЕсли F – первообразная для f на отрезке [a; b], то Формула Ньютона - ЛейбницаЕсли F – первообразная для f на отрезке [a; b], то](/img/thumbs/bd75d28b1ccbaffe66994b74d6b79716-800x.jpg)







