Выполнила: Асланбекова Марьям, ученица 9 А класса.
Научный руководитель: Асланбекова Лида Сайдаровна,
учитель математики МБОУ «СОШ №50» г. Грозного.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Гипотеза Пуанкаре или доказательство на миллион
Содержание
- 1. Презентация по математике на тему Гипотеза Пуанкаре или доказательство на миллион
- 2. Люди, равнодушные к математике, глухие к ней,
- 3. Актуальность работыЧасто, беседуя со старшеклассниками об исследовательских
- 4. Объект исследования: Гипотеза ПуанкареПредмет исследования: Топология
- 5. Выдвижение гипотезыНеужели гипотеза Пуанкаре(доказательство Перельмана) подтверждает теоретические
- 6. Основополагающий вопросВсе ли великие открытия в математике сделаны, а теоремы доказаны?
- 7. Цели работыВыявить неисследованные области математики;Познакомиться с величайшими математическими задачами тысячелетия;Поделиться информацией со своими сверстниками.
- 8. Задачи Провести социологический опрос;Изучить гипотезу Пуанкаре;Познакомиться с
- 9. Социологический опросВо время исследований я провела социологический
- 10. Онлайн-анкетаА также на сайте я разместила онлайн-анкету «Задачи Тысячелетия», на которую ребята могут ответить по ссылке:http://anketolog.ru/s/118101/qjlOsbIs
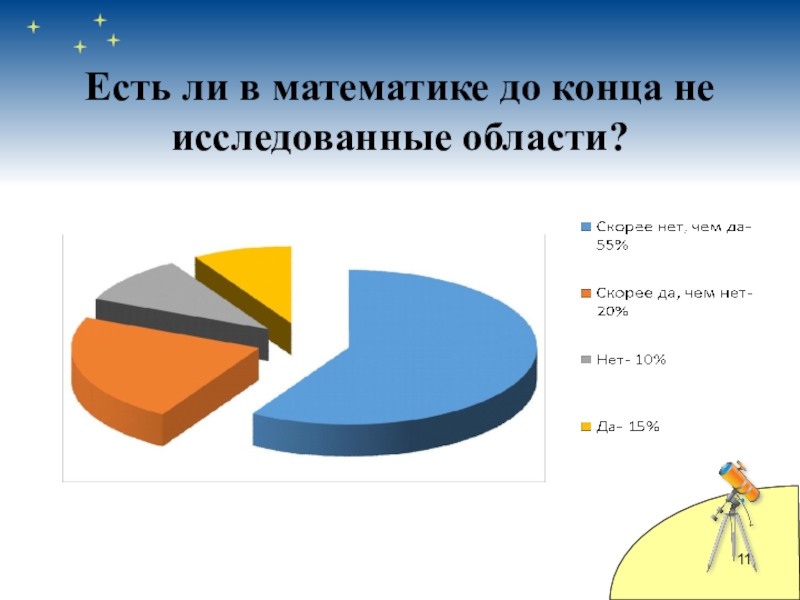
- 11. Есть ли в математике до конца не исследованные области?
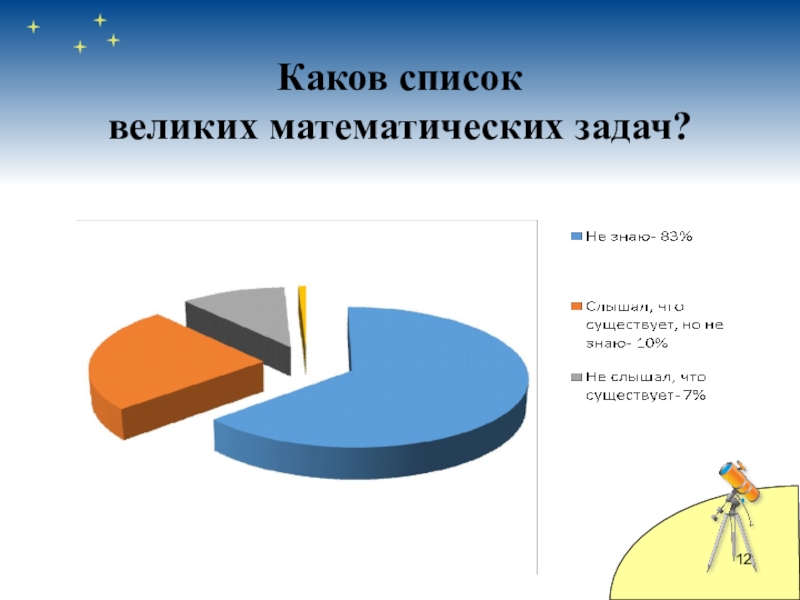
- 12. Каков список великих математических задач?
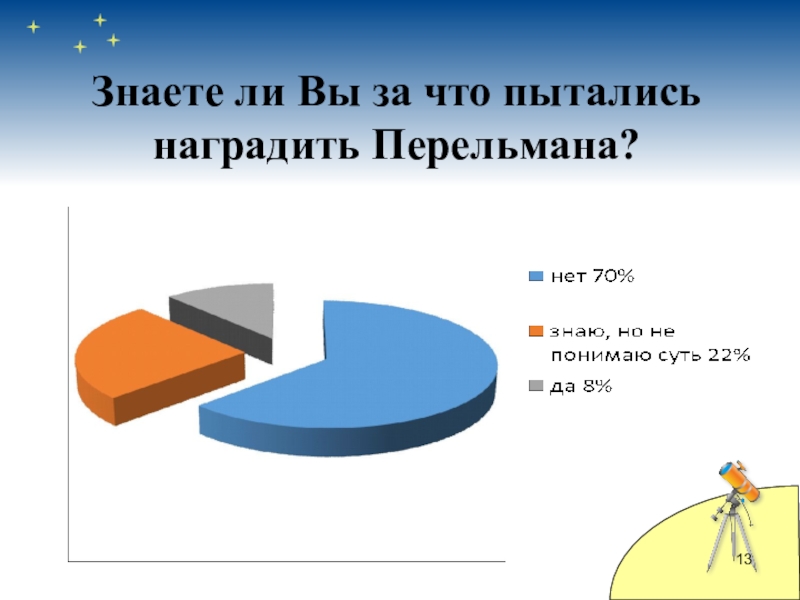
- 13. Знаете ли Вы за что пытались наградить Перельмана?
- 14. Анализ анкетированияСудя по результатам анкетирования, многие
- 15. Немного историиНачнем с 19 века.Жюль Анри Пуанкаре (1854
- 16. Одни из самых крупных достижений ПуанкареСоздание топологии.Разработка новых,
- 17. Гипотеза Пуанкаре«Всякое компактное трехмерное многообразие без края
- 18. Объясняя гипотезу Пуанкаре, начинают так: представьте себе
- 19. Грусть на лице этого животного является следствием
- 20. Что такое топология?Топологию часто определяют как «резиновую
- 21. Доказательство длиною в век…Cогласно гипотезе Пуанкаре,
- 22. Григорий Перельман. Как не стать миллионером.
- 23. Значение гипотезы Пуанкаре "Формулой Вселенной" утверждение Пуанкаре называют
- 24. Семь величайших математических загадок тысячелетияСписок получил
- 25. Уравнение Навье-Стокса Решения этих уравнений неизвестны, и при
- 26. Гипотеза Римана Считается, что распределение простых чисел среди натуральных
- 27. Гипотеза Пуанкаре* Всякое односвязное замкнутое трехмерное многообразие гомеоморфно трехмерной сфере. *Доказана Григорием Перельманом.
- 28. Гипотеза Ходжа В ХХ веке математики открыли
- 29. Теория Янга-МиллсаУравнения квантовой физики описывают мир элементарных
- 30. Гипотеза Берча и Свиннертона-Дайера Связана с описанием
- 31. Проблема Кука Допустим, находясь в большой компании,
- 32. Выводы Математика является необъятной наукой.В школе нужно всячески
- 33. Практическое применение работы Моя работа может бытьИнтересна
- 34. ЗаключениеГипотеза подтвердилась: действительно, в математике есть много
- 35. ЛитератураБолтянский В.Г., Ефремович В. А. Наглядная топология. — М.:
- 36. Спасибо за внимание.Мною изготовлен информационный буклет-приложение.
Люди, равнодушные к математике, глухие к ней, всегда казались мне калеками! Они беднее на целый мир - такой мир! Они даже не догадываются, что он существует!
Слайд 1 «Шаги в науку-2014» Научно-исследовательская работа по математике «Пластилиновая» гипотеза или доказательство на
миллион
Слайд 2Люди, равнодушные к математике, глухие к ней, всегда казались мне калеками!
Они беднее на целый мир - такой мир! Они даже не догадываются, что он существует!
С. Лем
С. Лем
Слайд 3Актуальность работы
Часто, беседуя со старшеклассниками об исследовательских работах по математике, слышу
следующее: "Что можно нового открыть в математике?". А действительно: может быть все великие открытия сделаны, а теоремы уже доказаны?
Проблема, о которой пойдет речь, выбивается из ряда других проблем математики 2000 года: лишь она одна считается уже решенной. Приоритет Григория Перельмана - нашего соотечественника, доказавшего гипотезу Пуанкаре, - неоспорим, его доказательство признано ведущими экспертами мира. Об этой почти детективной истории я узнала недавно. К своему великому удивлению, узнала, что в мире математики существует определенный ряд загадок, которые ждут своего часа.
Проблема, о которой пойдет речь, выбивается из ряда других проблем математики 2000 года: лишь она одна считается уже решенной. Приоритет Григория Перельмана - нашего соотечественника, доказавшего гипотезу Пуанкаре, - неоспорим, его доказательство признано ведущими экспертами мира. Об этой почти детективной истории я узнала недавно. К своему великому удивлению, узнала, что в мире математики существует определенный ряд загадок, которые ждут своего часа.
Слайд 5Выдвижение гипотезы
Неужели гипотеза Пуанкаре(доказательство Перельмана) подтверждает теоретические предположения ученых о строении
Вселенной со времен создания мира!
Гипотеза Пуанкаре настолько сложна для понимания простому обывателю, что я взяла на себя смелость изучить самой и рассказать о ней и других математических задачах тысячелетия своим сверстникам.
Таким образом, ко мне пришла идея о создании этого проекта.
Гипотеза Пуанкаре настолько сложна для понимания простому обывателю, что я взяла на себя смелость изучить самой и рассказать о ней и других математических задачах тысячелетия своим сверстникам.
Таким образом, ко мне пришла идея о создании этого проекта.
Слайд 7Цели работы
Выявить неисследованные области математики;
Познакомиться с величайшими математическими задачами тысячелетия;
Поделиться информацией
со своими сверстниками.
Слайд 8Задачи
Провести социологический опрос;
Изучить гипотезу Пуанкаре;
Познакомиться с топологией;
Рассмотреть доказательство Перельмана;
Исследовать роль
гипотезы Пуанкаре в изучении космоса и строении мироздания;
Изготовить информационный буклет.
Изготовить информационный буклет.
Слайд 9Социологический опрос
Во время исследований я провела социологический опрос, чтобы понять, насколько
мои сверстники знакомы с данной темой. Было проведено анкетирование среди учащихся МБОУ«СОШ №50».
Слайд 10Онлайн-анкета
А также на сайте
я разместила онлайн-анкету «Задачи Тысячелетия», на которую
ребята могут ответить по ссылке:
http://anketolog.ru/s/118101/qjlOsbIs
http://anketolog.ru/s/118101/qjlOsbIs
Слайд 14 Анализ анкетирования
Судя по результатам анкетирования, многие практически не посвящены в
вопросы, математических задач тысячелетия. Но порадовали ответы оптимистично настроенных и заинтересованных ребят. Это дает мне стимул для дальнейших исследований.
Слайд 15Немного истории
Начнем с 19 века.
Жюль Анри Пуанкаре (1854 – 1912) французский математик, физик, астроном и
философ. В 1887 году Пуанкаре представил работу на математический конкурс, посвященный 60-летию короля Швеции Оскара II. В ней обнаружилась ошибка, которая привела к появлению теории хаоса.
В 1904 году он сформулировал гипотезу уже в современном виде.
Независимо от Эйнштейна выдвинул основные положения специальной теории относительности. Он считается учёным, способным охватить все математические результаты своего времени. Его перу принадлежат более 500 статей и книг.
Слайд 16Одни из самых крупных достижений Пуанкаре
Создание топологии.
Разработка новых, чрезвычайно эффективных методов небесной механики.
Создание
математических основ теории относительности.
В 1900 г. сформулировал топологическую характеристику объекта, названную гомотопией*.
В 1900 г. сформулировал топологическую характеристику объекта, названную гомотопией*.
Слайд 17Гипотеза Пуанкаре
«Всякое компактное трехмерное многообразие без края гомеоморфно трехмерной сфере».
Простыми словами
гипотезу Пуанкаре можно изложить так: если трехмерная поверхность в чем-то похожа на сферу, то ее можно расправить сферу.
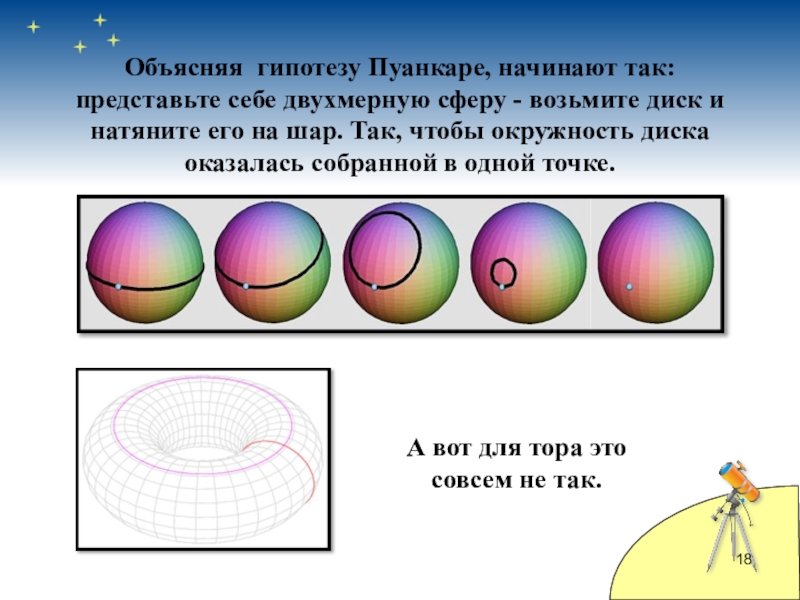
Слайд 18Объясняя гипотезу Пуанкаре, начинают так: представьте себе двухмерную сферу - возьмите
диск и натяните его на шар. Так, чтобы окружность диска оказалась собранной в одной точке.
А вот для тора это
совсем не так.
Слайд 19Грусть на лице этого животного является следствием осознания того, что желаемый
кусочек сыра находится на нестягиваемой петле.
Слайд 20Что такое топология?
Топологию часто определяют как «резиновую геометрию», т.е. как науку
о свойствах геометрических фигур, которые не меняются при плавных деформациях без разрывов и склеек. Главную идею проще всего объяснить на классическом примере кружки и бублика. Кружку можно превратить в бублик непрерывной деформацией.
Слайд 21 Доказательство длиною в век…
Cогласно гипотезе Пуанкаре, трехмерная сфера - это
единственная трехмерная штуковина, поверхность которой может быть стянута в одну точку неким гипотетическим «гипершнуром». Жюль Анри Пуанкаре предположил такое в 1904 году. Теперь Перельман убедил всех понимающих, что французский тополог был прав. И превратил его гипотезу в теорему. Доказательство помогает понять, какая форма у нашей Вселенной. И позволяет весьма обоснованно предположить, что она и есть та самая трехмерная сфера. Но если Вселенная – такая «фигура», которую можно стянуть в точку, то, наверное, можно и растянуть из точки. Что служит косвенным подтверждением теории Большого взрыва, которая утверждает: как раз из точки Вселенная и произошла.
Слайд 22Григорий Перельман. Как не стать миллионером.
В 2002-2003 годах
русский математик Григорий Перельман опубликовал в интернете доказательство гипотезы Пуанкаре, которое не давалось ни одному из его коллег в течение почти ста лет. Перельмана ждали слава, многочисленные награды и приз в $1 млн, назначенный за решение этой задачи благотворительным Институтом Клэя. Перельман, однако, отказался и от почестей и от денег, а через несколько лет и вовсе ушел из математики. На вопрос о миллионе, который так волновал всех удивлённых и любопытных, Перельман ответил: «Я знаю, как управляют Вселенной. И скажите – зачем же мне бежать за миллионом?» Кинокомпания «Президент-фильм» с согласия Перельмана планирует снять о нем художественную ленту «Формула Вселенной».
Слайд 23Значение гипотезы Пуанкаре
"Формулой Вселенной" утверждение Пуанкаре называют из-за его важности в
изучении сложных физических процессов в теории мироздания и из-за того, что оно дает ответ на вопрос о форме Вселенной. Играет свою роль это открытие и в развитии нанотехнологий. Доказательство гипотезы Пуанкаре важно не только в описании формы Вселенной, но и помогает сделать прорыв в развитии теории происхождения Вселенной.
Слайд 24Семь величайших математических
загадок тысячелетия
Список получил название
Millennium Prize Problems.
Институт математики Клея объявил о награде в $1 млн за решение каждой из этих главных математических проблем.
24 мая 2000 года эксперты института выбрали семь проблем - по числу миллионов долларов, выделенных на премии.
24 мая 2000 года эксперты института выбрали семь проблем - по числу миллионов долларов, выделенных на премии.
Слайд 25Уравнение Навье-Стокса
Решения этих уравнений
неизвестны, и при этом даже неизвестно, как
их решать. Необходимо показать, что решение существует и является достаточно гладкой функцией. Это позволит существенно изменить способы проведения гидро- и аэродинамических расчетов.
Слайд 26Гипотеза Римана
Считается, что распределение
простых чисел среди натуральных не подчиняется никакой закономерности.
Однако немецкий математик Риман высказал предположение, касающееся свойств последовательности простых чисел. Если гипотеза Римана будет доказана, то это приведет к революционному изменению наших знаний в области шифрования и к невиданному прорыву в области безопасности Интернета.
Слайд 27Гипотеза Пуанкаре*
Всякое односвязное замкнутое трехмерное многообразие гомеоморфно трехмерной сфере.
*Доказана
Григорием Перельманом.
Слайд 28Гипотеза Ходжа
В ХХ веке математики
открыли мощный метод исследования формы
сложных объектов - использование вместо самого объекта простых "кирпичиков", которые склеиваются между собой и образуют его подобие. Гипотеза Ходжа связана с некоторыми предположениями относительно свойств таких "кирпичиков" и объектов.
Слайд 29Теория Янга-Миллса
Уравнения квантовой физики описывают мир элементарных частиц. Физики Янг и Миллс, обнаружив связь между
геометрией и физикой элементарных частиц, написали свои уравнения. Тем самым они нашли путь к объединению теорий электромагнитного, слабого и сильного взаимодействий. Из уравнений Янга-Миллса следовало существование частиц, которые действительно наблюдались в лабораториях, поэтому теория Янга - Миллса принята большинством физиков, несмотря на то, что в рамках этой теории до сих пор не удается предсказывать массы элементарных частиц.
Слайд 30Гипотеза Берча и Свиннертона-Дайера
Связана с описанием множества
решений некоторых алгебраических
уравнений от нескольких переменных с целыми коэффициентами.
Примером подобного уравнения является выражение
x2 + y2 = z2.
Примером подобного уравнения является выражение
x2 + y2 = z2.
Слайд 31Проблема Кука
Допустим, находясь в большой компании,
Вы хотите убедиться что
там же находится Ваш знакомый. Если Вам скажут, что он сидит в углу, то Вам достаточно доли секунды, чтобы, бросив взгляд, убедиться в истинности информации. В отсутствии этой информации Вы будете вынуждены обойти всю комнату, рассматривая гостей. Эти примеры иллюстрируют общие явления: решение какой-либо задачи часто занимает больше времени, чем проверка правильности решения. Стивен Кук сформулировал проблему: может ли проверка правильности решения задачи быть более длительной, чем само получение решения, независимо от алгоритма проверки.
Слайд 32Выводы
Математика является необъятной наукой.
В школе нужно всячески повышать познавательный интерес
учащихся к математике.
Все средства массовой информации должны способствовать появлению интереса к математике у молодежи, как к самой перспективной науке.
Не все открытия в математике сделаны и не все теоремы доказаны.
Спешите их осталось еще 6!!!
Все средства массовой информации должны способствовать появлению интереса к математике у молодежи, как к самой перспективной науке.
Не все открытия в математике сделаны и не все теоремы доказаны.
Спешите их осталось еще 6!!!
Слайд 33Практическое
применение работы
Моя работа может быть
Интересна учащимся увлеченным математикой.
Использована на факультативных
занятиях.
Применена в работе математического кружка.
Наглядным материалом на уроках для активации познавательного интереса к математике у учащихся.
Применена в работе математического кружка.
Наглядным материалом на уроках для активации познавательного интереса к математике у учащихся.
Слайд 34Заключение
Гипотеза подтвердилась: действительно, в математике есть много нерешенных задач и недоказанных
теорем. Впереди нас ждут уникальные эксперименты, научные открытия, прорывы в самых современных научных сферах. Главное, чтобы это давало дополнительный стимул развития нашей стране. Как бы ни сложилось мое будущее, какую бы профессию не выбрала, я уверена, что работа над этим проектом является для меня первым, но уже уверенным шагом в мир большой науки.
Мы надеемся, что задачи тысячелетия будут решены в ближайшее время и это принесет мировой науке только пользу!!!
Мы надеемся, что задачи тысячелетия будут решены в ближайшее время и это принесет мировой науке только пользу!!!
Слайд 35Литература
Болтянский В.Г., Ефремович В. А. Наглядная топология. — М.: Наука, 1982.
Васильев В.А. Введение
в топологию. — М.: ФАЗИС, 1997.
Вербицкий М. Лекции и задачи по топологии. — 2009.
Виро О.Я., Иванов О.А., Харламов В.М., Нецветаев,Н.Ю. Элементарная топология. — 2007.
Коснёвски Ч. Начальный курс алгебраической топологии. — М.: Мир, 1983.
Милнор Дж., Уоллес А. Дифференциальная топология. Начальный курс. — М.: Мир, 1972.
Милнор Дж., Сташеф Дж. Характеристические классы. — М.: Мир, 1979.
Прасолов В.В. Наглядная топология. — М.: МЦНМО, 1995.
Стюарт Я. Топология.Стюарт Я. Топология. // Квант, № 7, 1992.
Топология, видео.
Интернет-ресурсы.
Вербицкий М. Лекции и задачи по топологии. — 2009.
Виро О.Я., Иванов О.А., Харламов В.М., Нецветаев,Н.Ю. Элементарная топология. — 2007.
Коснёвски Ч. Начальный курс алгебраической топологии. — М.: Мир, 1983.
Милнор Дж., Уоллес А. Дифференциальная топология. Начальный курс. — М.: Мир, 1972.
Милнор Дж., Сташеф Дж. Характеристические классы. — М.: Мир, 1979.
Прасолов В.В. Наглядная топология. — М.: МЦНМО, 1995.
Стюарт Я. Топология.Стюарт Я. Топология. // Квант, № 7, 1992.
Топология, видео.
Интернет-ресурсы.