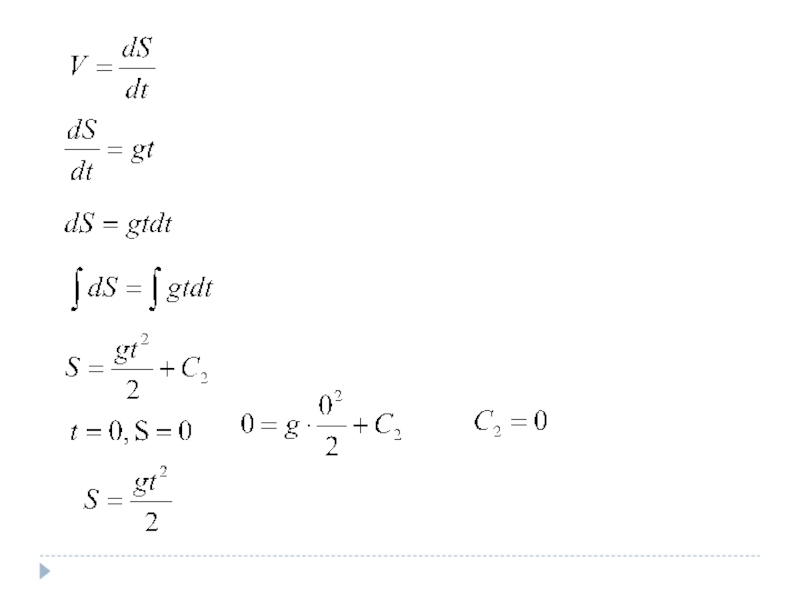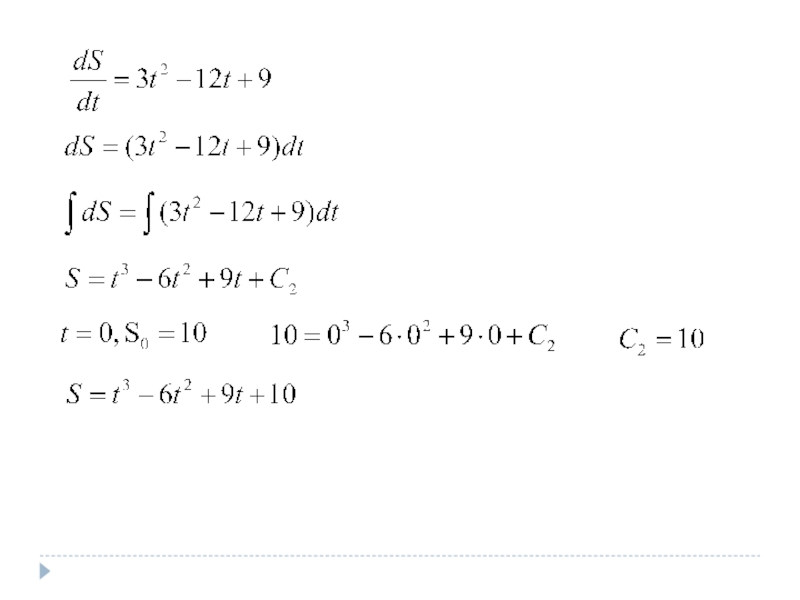- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Геометрическое и физическое приложение неопределенного интеграла
Содержание
- 1. Презентация по математике на тему Геометрическое и физическое приложение неопределенного интеграла
- 2. Цель урока:Формирование представлений о геометрическом и физическом
- 3. 1. Нахождение первообразной по начальным условиям.При интегрировании
- 4. Примеры.Найти функцию, производная которой: y′=3x² - 6x +2.Решение.
- 5. 2. Найти функцию, производная которой: y′=2x –
- 6. 3. Найти ∫(cos x – sin x)dx, если при x=π/2 значение первообразной функции равно 6.Решение.
- 7. 2. Выделение из семейства кривых с одинаковым
- 8. Этому уравнению на плоскости соответствует бесконечное множество
- 9. Примеры.Найти уравнение кривой, если угловой коэффициент касательной
- 10. 2. Составить уравнение линии, если угловой коэффициент
- 11. 3. Найти уравнение кривой, проходящей через точку
- 12. 3. Составление уравнения движения тела по заданному
- 13. Примеры.1. Скорость прямолинейного движения точки изменяется по
- 14. 2. Скорость прямолинейного движения точки изменяется по
- 15. 3. Найти закон движения свободно падающего тела
- 16. Слайд 16
- 17. 4. Точка движется прямолинейно с ускорением a=6t–12.
- 18. Слайд 18
- 19. 2) При t=2 c:3) Исследуем функцию, определяющую
Слайд 1Геометрическое и физическое приложение неопределенного интеграла.
Преподаватель ГАПОУ «ЛНТ»
Шаммасова А.А.
Слайд 2Цель урока:
Формирование представлений о геометрическом и физическом приложениях неопределенного интеграла.
Формирование умений
Слайд 31. Нахождение первообразной по начальным условиям.
При интегрировании функции получается совокупность (множество)
С может принимать любые числовые значения, если на первообразную функцию не наложено никаких начальных условий.
Чтобы из множества первообразных функций выделить одну определенную функцию, должны быть заданы начальные условия.
Начальные условия – это задание частных значений x и y для первообразной функции y=F(x)+C, по которым находится определенное значение С, удовлетворяющее этим начальным условиям.
Слайд 52. Найти функцию, производная которой: y′=2x – 3, если при x=2
Решение.
Слайд 72. Выделение из семейства кривых с одинаковым наклоном линии, проходящей через
Вспомним:
Наклон k кривой y=(x) – угловой коэффициент касательной – это тангенс угла наклона касательной к этой кривой в данной точке. Он равен значению производной в этой точке: k=y′.
Обратная задача:
Зная наклон k кривой в любой ее точке как функцию абсциссы этой точки: k=f(x), найти уравнение кривой.
Получили уравнение, содержащее произвольную постоянную С.
Слайд 8Этому уравнению на плоскости соответствует бесконечное множество кривых (семейство кривых), уравнения
Графики функций, получающихся в результате интегрирования, называются интегральными кривыми.
Каждый интеграл дает семейство интегральных кривых. Интегральные кривые одного семейства имеют одну и ту же форму и смещены друг относительно друга по вертикали. Сдвиг кривой зависит от постоянной С.
Из семейства этих кривых, имеющих один и тот же наклон, нам нужно уметь выделять ту, которая проходит через данную точку.
Слайд 9Примеры.
Найти уравнение кривой, если угловой коэффициент касательной в каждой ее точке
Решение.
k=2x
Мы нашли семейство кривых, для которых угловой коэффициент касательной в любой точке равен 2x. Эти кривые отличаются друг от друга на постоянное слагаемое С. При С=0 получим параболу y=x² с вершиной в начале координат, при С=1 – параболу y=x²+1 с вершиной в точке (0;1), при С=-2 – параболу y=x²-2 с вершиной в точке (0;-2) и т.д.
Слайд 102. Составить уравнение линии, если угловой коэффициент касательной в любой точке
Решение.
k=y/x
Потенцируя, получим: y=Cx – уравнение семейств прямых, проходящих через начало координат.
Слайд 113. Найти уравнение кривой, проходящей через точку А(0;1), у которой касательная
Решение.
Слайд 123. Составление уравнения движения тела по заданному уравнению скорости или ускорения
Вспомним (из дифференциального исчисления):
V=S′(t) – скорость движущегося тела
a(t)=V′(t)=S′′(t) – ускорение движущегося тела
S(t) – путь
Тогда закон движения тела S(t) по заданной скорости можно найти интегрированием, а по заданному ускорению – двукратным интегрированием.
Слайд 13Примеры.
1. Скорость прямолинейного движения точки изменяется по закону V=3t² - 2t.
Решение.
Слайд 142. Скорость прямолинейного движения точки изменяется по закону V=3t² +4. Найти
Решение.
Слайд 153. Найти закон движения свободно падающего тела при постоянном ускорении g,
Решение.
Слайд 174. Точка движется прямолинейно с ускорением a=6t–12. В момент времени t=0
Решение.
1)
Слайд 192) При t=2 c:
3) Исследуем функцию, определяющую изменение скорости, на максимум
Следовательно, скорость является наименьшей при t=2 с.