- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Элементарные функции, их свойства и графики
Содержание
- 1. Презентация по математике на тему Элементарные функции, их свойства и графики
- 2. Две взаимно перпендикулярные числовые оси с общим
- 3. Координатная плоскость делится осями на четыре части,
- 4. Пусть М - произвольная точка координатной плоскости.Координата
- 5. Функция может быть задана с помощью ее
- 6. Свойства функцииЧисловое множество называется симметричным относительно начала
- 7. Свойства функции2) Для любого x из области
- 8. Свойства функцииIV. Промежутки знакопостоянства функции. Промежутки в
- 9. Линейная функцияЛинейной называется функция вида у =
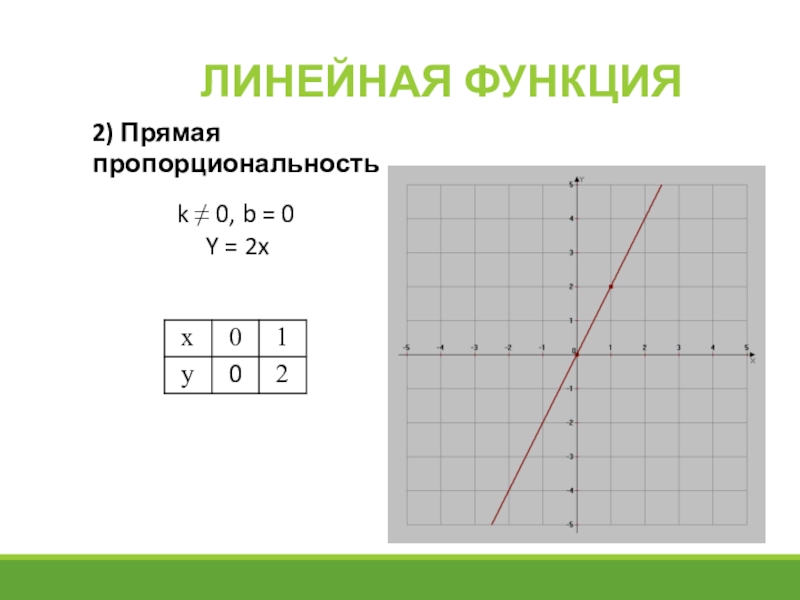
- 10. Линейная функция2) Прямая пропорциональность k 0, b = 0Y = 2x
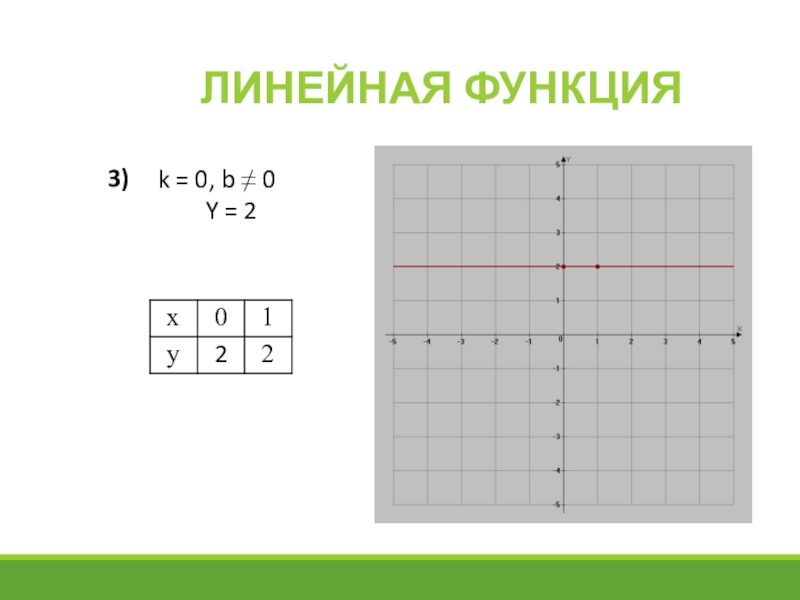
- 11. Линейная функция3) k = 0, b 0Y = 2
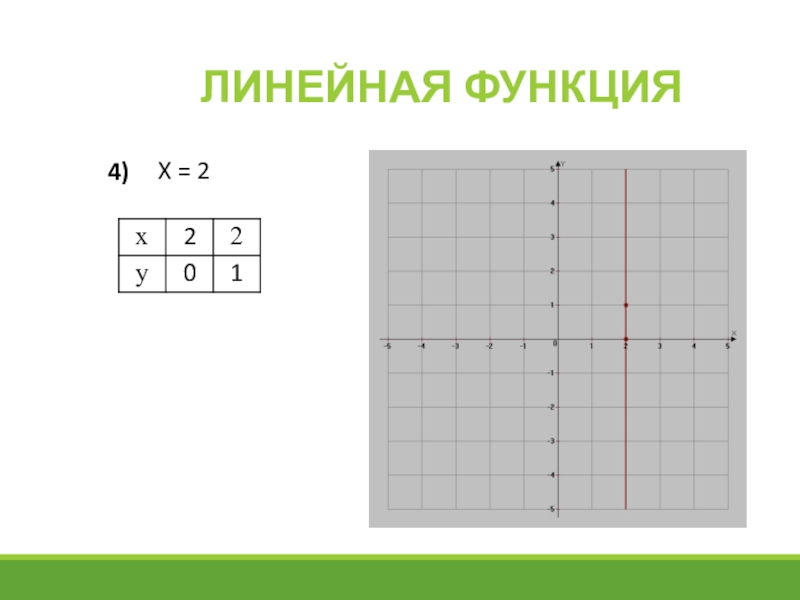
- 12. Линейная функция4) X = 2
- 13. Квадратичная функция
- 14. Квадратичная функция
- 15. Квадратичная функцияПостроим график функцииa = 1, ветви
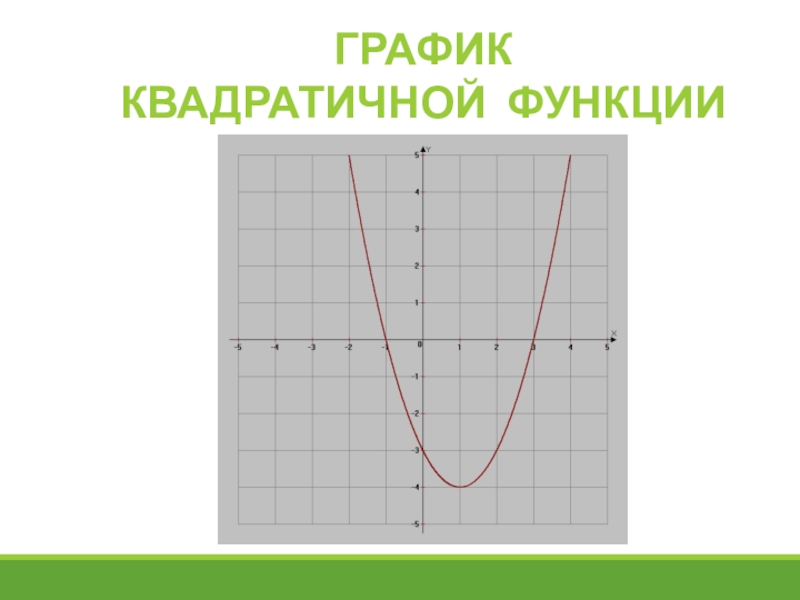
- 16. ГрафикКвадратичной функции
- 17. Кубическая функцияГрафик функции — кубическая параболаСоставим таблицу
- 18. график функции
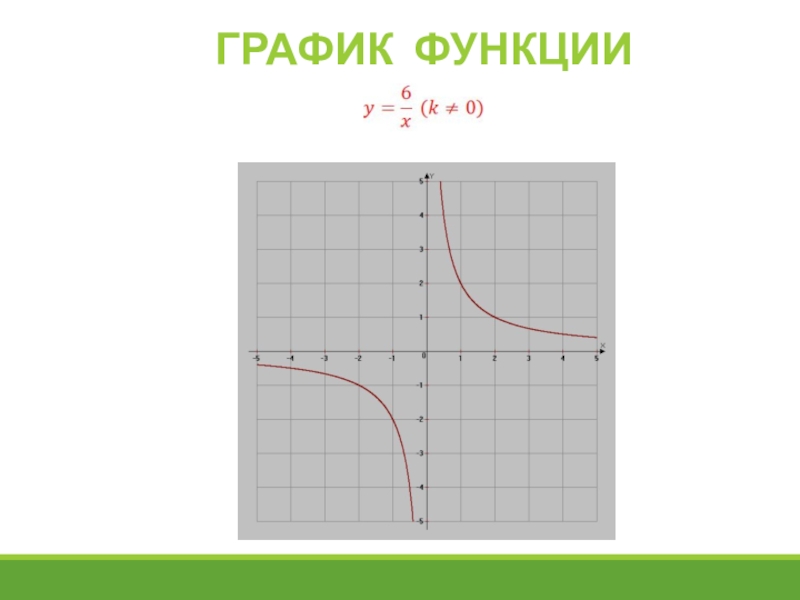
- 19. функцияГрафик функции — гипербола.При построении графика функции
- 20. Нулей нет.Промежутки монотонности:Если k>0, то функция убывает
- 21. график функции
- 22. функцияПри построении графика удобно брать те значения
- 23. График функции
- 24. Слайд 24
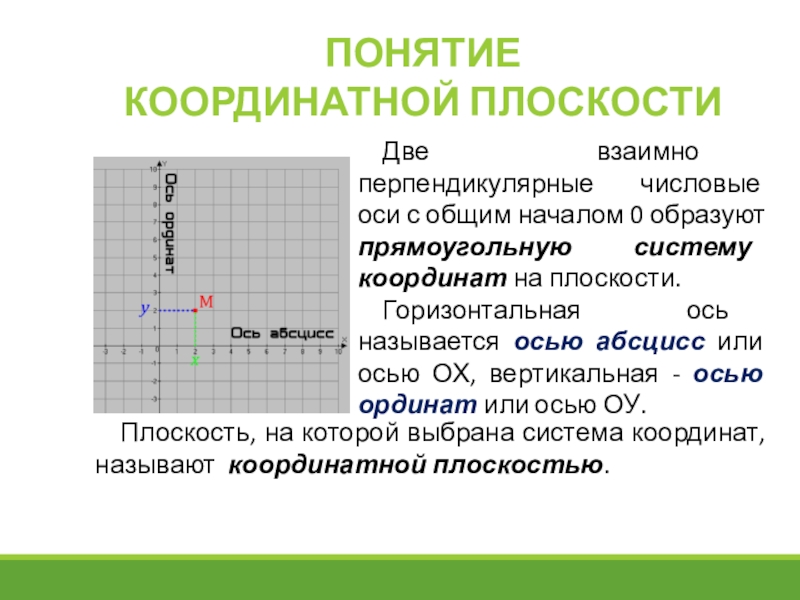
Слайд 2Две взаимно перпендикулярные числовые оси с общим началом 0 образуют прямоугольную
Горизонтальная ось называется осью абсцисс или осью ОХ, вертикальная - осью ординат или осью ОУ.
Плоскость, на которой выбрана система координат, называют координатной плоскостью.
Понятие
координатной плоскости
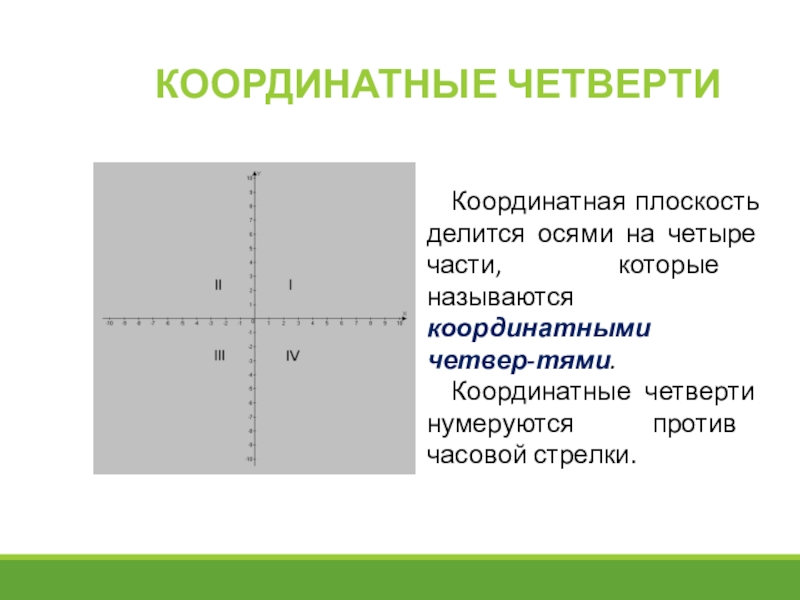
Слайд 3Координатная плоскость делится осями на четыре части, которые называются координатными четвер-тями.
Координатные
координатные четверти
Слайд 4Пусть М - произвольная точка координатной плоскости.
Координата проекции точки М на
Абсциссу и ординату точки М называют координатами точки М. При этом записывают М (х, у) (на первом месте всегда пишут абсциссу).
! Каждой паре чисел х и у соответствует единственная точка М координатной плоскости с координатами (х, у). Значит, координаты х и у определяют положение точки на плоскости.
Точка на координатной
плоскости
Слайд 5Функция может быть задана с помощью ее графика.
На координатной плоскости 0ХУ
Графический способ
Задания функции
Слайд 6Свойства функции
Числовое множество называется симметричным относительно начала координат, если этому множеству
Функция у = f(x) называется
если выполняются два условия:
1)
Слайд 7Свойства функции
2) Для любого x из области определения функции выполняется равенство:
III. Возрастание и убывание функции
Функция у = f(х) называется возрастающей (убывающей) на некотором промежутке, если для любых двух значений х из этого промежутка большему значению аргумента соответствует большее (меньшее) значение функции, т.е. из условия х1< х2 следует, что f(х1)
Слайд 8Свойства функции
IV. Промежутки знакопостоянства функции. Промежутки в которых функция сохраняет свой
V. Нули функции.
Значения аргумента х в которых f(х)=0 называются нулями функции.
Слайд 9Линейная функция
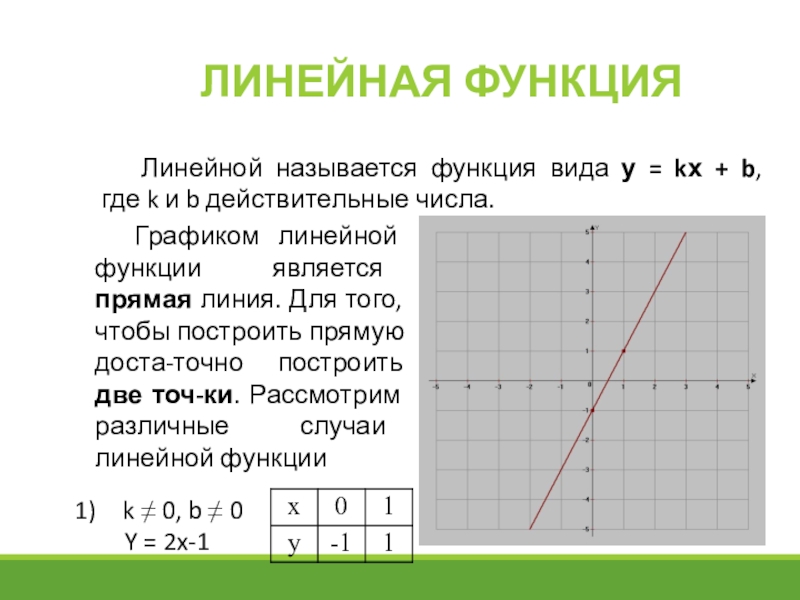
Линейной называется функция вида у = kх + b,
где
k 0, b 0
Y = 2x-1
Графиком линейной функции является прямая линия. Для того, чтобы построить прямую доста-точно построить две точ-ки. Рассмотрим различные случаи линейной функции
Слайд 15Квадратичная функция
Построим график функции
a = 1, ветви параболы направлены вверх
Найдем координаты
Ось симметрии параболы x = 1
Найдем координаты точек пересечения с осью ОХ. Для этого решим уравнение
Координаты точки пересечения с осью OY x=0; y = -3;
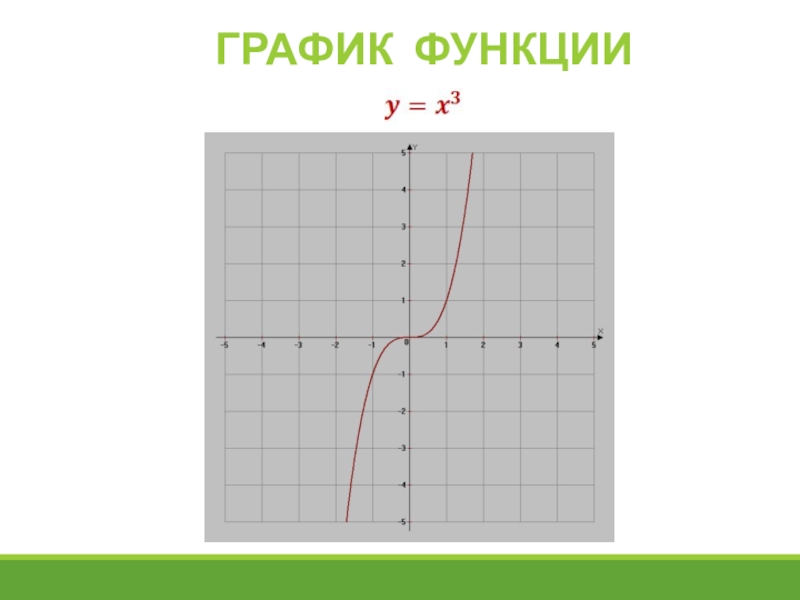
Слайд 17Кубическая функция
График функции — кубическая парабола
Составим таблицу значения функции в 5-ти
Свойства функции y=x3
Область определения: множество всех действительных чисел
Множество значений: множество всех действительных чисел
Функция нечетная
Нули функции: y=0 при x=0
Функция возрастает на всей области определения
Слайд 19функция
График функции — гипербола.
При построении графика функции удобно брать те значения
Если k<0, то график функции расположен во II и IV координатных областях
Свойства функции:
Область определения: промежутки (-; 0) и (0; )
Множество значений: x0
Функция нечетная.
Слайд 20Нулей нет.
Промежутки монотонности:
Если k>0, то функция убывает на промежутках
(-; 0)
Если k<0, то функция возрастает на промежутках (-; 0) и (0; )
Промежутки знакопостоянства
Если k>0, то
Если k<0, то
Свойства функции
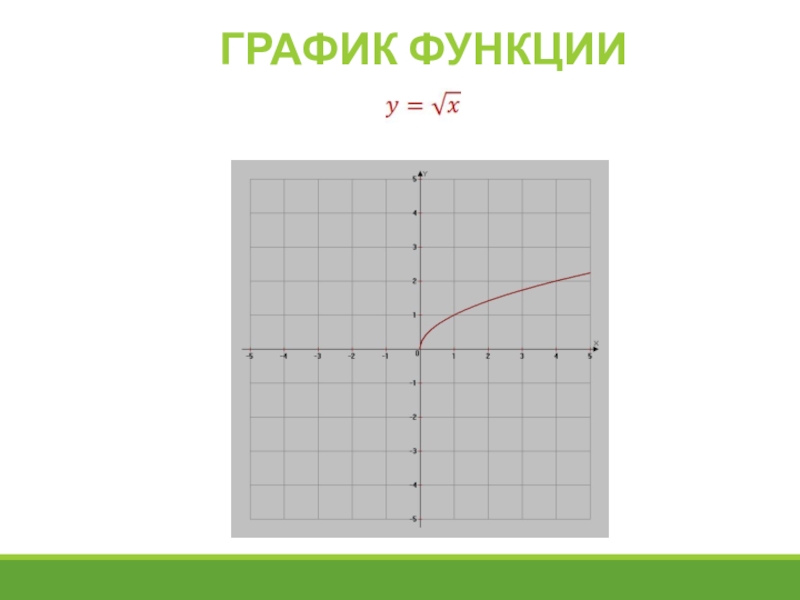
Слайд 22функция
При построении графика удобно брать те значения аргумента, из которых легко
Свойства функции:
Область определения: x0
Множество значений: y0
Функция не является четной и не является нечетной
Нули: y=0, при x=0
Промежутки монотонности: функция возрастает на всей области определения
Промежутки знакопостоянства: y>0, при x>0