- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Арккосинус, арксинус
Содержание
- 1. Презентация по математике на тему Арккосинус, арксинус
- 2. xπ/2аSin-π/2arc sin a – a-11Арксинус числа а
- 3. Ищу число из отрезка [-π/2; π/2], синус которого равен …Вычислите:-π/2π/2
- 4. CosSin-11π0Арккосинус числа а , |а | ≤
- 5. Ищу число из отрезка [0; π], косинус которого равен…..Вычислите:
- 6. Имеет ли смысл выражение?аrcsin (-1/2)
- 7. Историческая справка. Современные обозначения arcsin и arccos
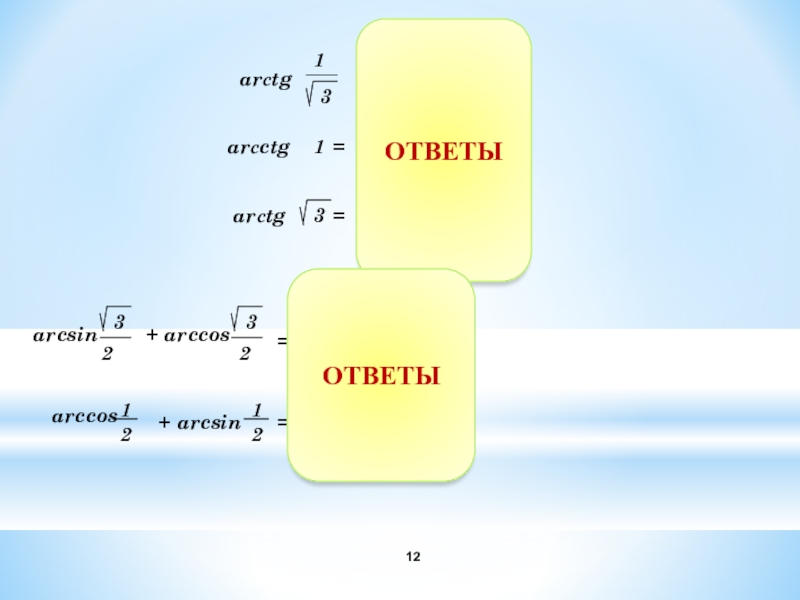
- 8. =arcsin1 =ОТВЕТЫ
- 9. ()()π ̶ ОТВЕТЫ
- 10. Арктангенс числа а есть число (угол) α
- 11. 0Арккотангенс числа а есть число (угол) α
- 12. +=+=ОТВЕТЫОТВЕТЫ
xπ/2аSin-π/2arc sin a – a-11Арксинус числа а , |а | ≤ 1 есть такое число α из промежутка [– π / 2; π / 2 ], синус которого равен числу а arc sin (– a)α– αarc
Слайд 1
Разработчик: Северинова С.Б.
Преподаватель математике ГБПОУ ВО «Павловский техникум»
Определение арксинуса,
арккосинуса
числа а
Слайд 2
x
π/2
а
Sin
-π/2
arc sin a
– a
-1
1
Арксинус числа а , |а | ≤
1 есть такое число α из промежутка [– π / 2; π / 2 ], синус которого равен числу а
arc sin (– a)
α
– α
arc sin (– a) = – arc sin a
Слайд 4
Cos
Sin
-1
1
π
0
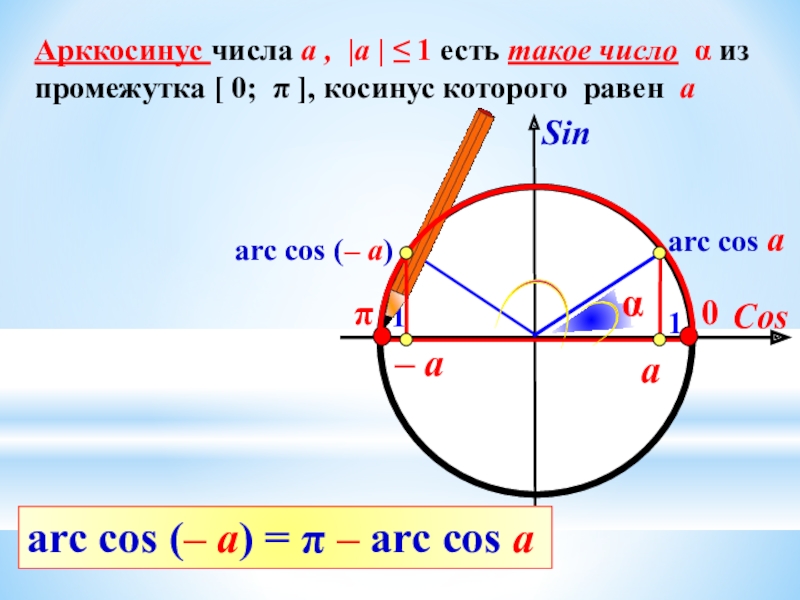
Арккосинус числа а , |а | ≤ 1 есть такое число
α из промежутка [ 0; π ], косинус которого равен а
а
arc cos a
arc соs (– a)
– a
α
arc cos (– a) = π – arc cos a
Слайд 6Имеет ли смысл выражение?
аrcsin (-1/2)
arccos arcsin
да нет нет
аrcsin 1,5 arccos arccos
нет да да
да нет нет
аrcsin 1,5 arccos arccos
нет да да
Слайд 7Историческая справка.
Современные обозначения arcsin и arccos появляются в 1772 в работах
великого математика Шерфера и известного французского ученого Ж.Л. Лагранжа, хотя несколько ранее их уже рассматривал Д. Бернули, который употреблял иную символику. Но общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга), что вполне согласуется со смыслом понятия: arcsin x, например, - это угол (а можно сказать и дуга), синус которого равен x.
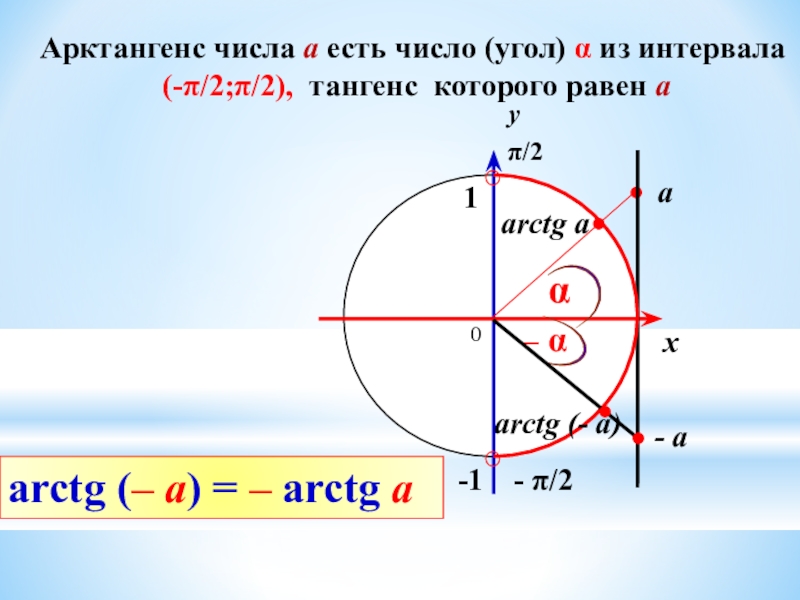
Слайд 10Арктангенс числа а есть число (угол) α из интервала
(-π/2;π/2), тангенс
которого равен а
arctg a
а
π/2
- π/2
у
х
α
– α
- а
arctg (- a)
arctg (– a) = – arctg a
Слайд 110
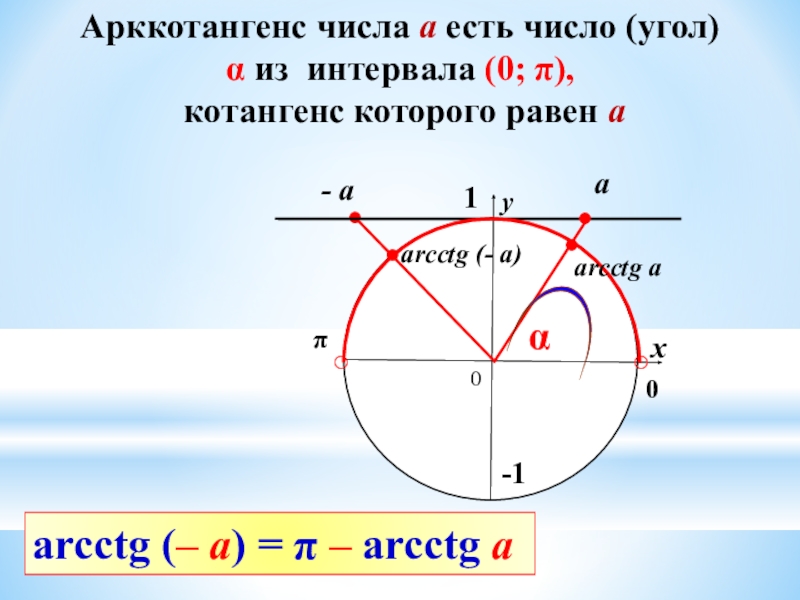
Арккотангенс числа а есть число (угол)
α из интервала (0; π),
котангенс которого равен а
а
arcctg (- a)
у
○
○
π
α
arcctg a
- а
arcctg (– a) = π – arcctg a


![Презентация по математике на тему Арккосинус, арксинус Ищу число из отрезка [-π/2; π/2], синус которого равен …Вычислите:-π/2π/2 Ищу число из отрезка [-π/2; π/2], синус которого равен …Вычислите:-π/2π/2](/img/thumbs/018cb064180497390fd3db7a3ee60542-800x.jpg)
![Презентация по математике на тему Арккосинус, арксинус Ищу число из отрезка [0; π], косинус которого равен…..Вычислите: Ищу число из отрезка [0; π], косинус которого равен…..Вычислите:](/img/thumbs/8250672c542014fcdc65931738cd600f-800x.jpg)