Вера Васильевна
2016 год
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Аликвотные дроби
Содержание
- 1. Презентация по математике на тему Аликвотные дроби
- 2. Необходимость в дробных числах
- 3. Первой дробью была половина
- 4. Единичные дроби встречаются в древнейших дошедших до нас математических текстах, составленных более 5000 лет тому назад
- 5. Египетская дробь — в математике сумма нескольких дробей вида 1/n
- 6. Древнем Египте математики «настоящими» дробями считали только аликвотные дроби
- 7. Египтяне все дроби записывали как суммы долей, то есть дробей вида 1/n.
- 8. Объект исследования: аликвотные дроби Цель исследования:
- 9. Происхождение аликвотных дробейЕгиптяне записывали все дроби
- 10. Египтяне ставили иероглиф «Глаз Хора» - единица для измерения ёмкостей и объемов, представляла собой дробь 63/64
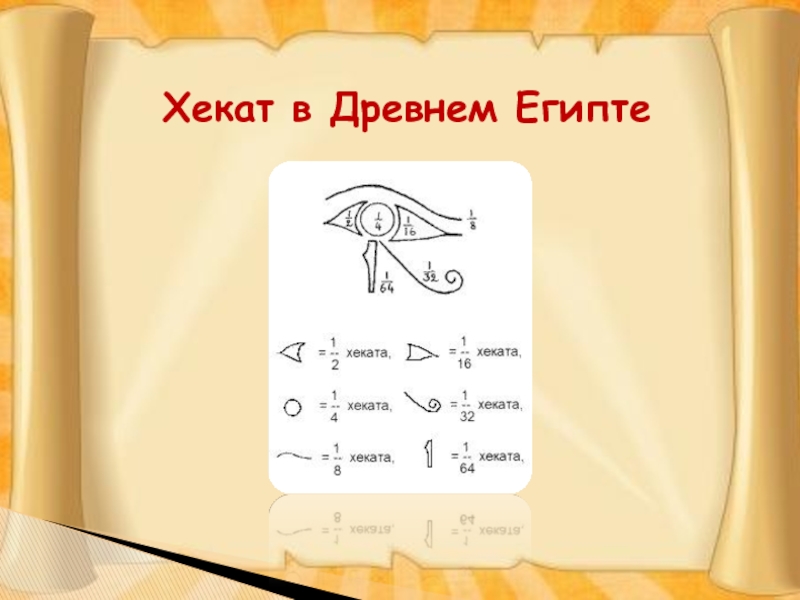
- 11. Хекат в Древнем Египте
- 12. Задача 1Разделить 7 хлебов между 8 людьми.
- 13. Математик VIII века Фибоначчи
- 14. Аликвотные струны
- 15. Представить число 2/43 в виде суммы аликвотных дробей2/43= 1/42 +1/86 +1/129 +1/301
- 16. Формула разложения дробей1/n=(1/(n+1)) +(1/n*(n+1))Примеры разложения дробей:1/3=1/(3+1)+1/3*(3+1)=1/4 +1/12;1/5=1/(5+1)+1/5*(5+1)=1/6 +1/30;1/8=1/(8+1)+1/8*(8+1)=1/9+ 1/72.
- 17. Преобразование дроби1/(n*(n+1)) =1/n -1/(n+1)1/6=1/(2*3)=1/2 -1/3½=1/(1*2) =1/1 -1/2
- 18. Доказательство равенства 1/n=(1/(n+1)) +(1/n*(n+1)) (1/(n+1)) +(1/n*(n+1)),
- 19. Задача 2Найди сумму1/2+1/(2*3)+1/(3*4)+1/(4*5)+…….+1/(19*20) =????Решение½=1/(1*2) =1/1 -1/21/6=1/(2*3)=1/2-1/31/12=1/(3*4)=1/3-1/41/20=1/(4*5) =1/4-1/5 и т.д.Подставив, уже разложенные выражения в наш пример, получаем:1/1-1/2+1/2-1/3+1/3-1/4+1/4-1/5……..+1/19-1/19-1/20=1/1-1/20=19/20.
- 20. Разложение 1 на слагаемые На 2 слагаемых1=1/2+1/2
- 21. Открытые проблемы Для всякого целого числа n ≥ 2, существуют положительные целые x, y и z такие, что4/n=1/x+ 1/y+ 1/zГипотеза Эрдёша-Страуса
- 22. Задача 3Представить число 1 в виде сумм
- 23. Задача 4Найди сумму1/(10*11)+1/(11*12)+…+1/(98*99)+1/(99*100)=?РешениеНайти сумму1/(1*2)+1/(2*3)+…+1/(98*99)+1/(99*100)=99/100И вычесть из нее сумму 1/(1*2)+1/(2*3)+…+1/(8*9)+1/(9*10)=9/1099/100-9/10 = (99-90)/100=9/100=0.09
- 24. Задача 5Чтобы узнать год празднования 100летия Российского
- 25. Заключение Разложение на три, четыре, пять и
- 26. Заключение Аликвотные дроби (с числителем 1) долгое
- 27. «Попал в дроби»
- 28. Спасибо за внимание!
Необходимость в дробных числах
Слайд 1Аликвотные дроби
Работу выполнил ученик 6 класса
МОУ «Яльгелевская школа»
Сапронов Дмитрий
Учитель: Дектярева
Слайд 4Единичные дроби встречаются в древнейших дошедших до нас математических текстах, составленных
более 5000 лет тому назад
Слайд 8Объект исследования: аликвотные дроби Цель исследования: Выяснить, какое значение имеют аликвотные дроби в нашей
жизни.
Задачи исследования:
Узнать происхождение аликвотных дробей.
Рассмотреть основные операции с аликвотными дробями.
Решать олимпиадные задачи с помощью
аликвотных дробей.
Составлять и решать задачи практического содержания.
Слайд 9
Происхождение аликвотных дробей
Египтяне записывали все дроби в виде суммы дробей.
Например,
8/15 = 1/3+1/5
Аликвотная дробь – это дробь вида 1/n (числитель – 1, а n – любое натуральное число).
Аликвотная дробь – это дробь вида 1/n (числитель – 1, а n – любое натуральное число).
Слайд 10Египтяне ставили иероглиф «Глаз Хора» - единица для измерения ёмкостей и
объемов, представляла собой дробь 63/64
Слайд 12Задача 1
Разделить 7 хлебов между 8 людьми. Если разрезать каждый хлеб
на 8 частей, придется провести 49 разрезов. А по-египетски эта задача решалась так:
7/8= 1/2 +1/4 +1/8.
Значит, каждому человеку дать пол хлеба, четверть хлеба и восьмушку хлеба. Придется сделать почти в три раза меньше разрезов.
7/8= 1/2 +1/4 +1/8.
Значит, каждому человеку дать пол хлеба, четверть хлеба и восьмушку хлеба. Придется сделать почти в три раза меньше разрезов.
Слайд 16Формула разложения дробей
1/n=(1/(n+1)) +(1/n*(n+1))
Примеры разложения дробей:
1/3=1/(3+1)+1/3*(3+1)=1/4 +1/12;
1/5=1/(5+1)+1/5*(5+1)=1/6 +1/30;
1/8=1/(8+1)+1/8*(8+1)=1/9+ 1/72.
Слайд 18Доказательство равенства
1/n=(1/(n+1)) +(1/n*(n+1))
(1/(n+1)) +(1/n*(n+1)), приведя дроби к общему знаменателю,
получаем:
(n+1)/((n+1)*n)
после сокращения получаем: 1/n.
Вывод: 1/n=1/n.
(n+1)/((n+1)*n)
после сокращения получаем: 1/n.
Вывод: 1/n=1/n.
Слайд 19Задача 2
Найди сумму
1/2+1/(2*3)+1/(3*4)+1/(4*5)+…….+1/(19*20) =????
Решение
½=1/(1*2) =1/1 -1/2
1/6=1/(2*3)=1/2-1/3
1/12=1/(3*4)=1/3-1/4
1/20=1/(4*5) =1/4-1/5 и т.д.
Подставив, уже разложенные
выражения в наш пример, получаем:
1/1-1/2+1/2-1/3+1/3-1/4+1/4-1/5……..+1/19-1/19-1/20=1/1-1/20=19/20.
1/1-1/2+1/2-1/3+1/3-1/4+1/4-1/5……..+1/19-1/19-1/20=1/1-1/20=19/20.
Слайд 20Разложение 1 на слагаемые
На 2 слагаемых
1=1/2+1/2
На 3 слагаемых
½=1/3+1/6 =½=1/3+1/6
=> 1=1/2+1/3+1/6
На 4 слагаемых
1/3=1/4+1/12 => 1=1/2+1/4+1/12+1/6
На 5 слагаемых
1/6=1/7+1/42 => 1=1/2+1/4+1/12+1/7+1/42
На 4 слагаемых
1/3=1/4+1/12 => 1=1/2+1/4+1/12+1/6
На 5 слагаемых
1/6=1/7+1/42 => 1=1/2+1/4+1/12+1/7+1/42
Слайд 21Открытые проблемы
Для всякого целого числа
n ≥ 2, существуют положительные целые x, y и z такие, что
4/n=1/x+
1/y+ 1/z
Гипотеза Эрдёша-Страуса
Слайд 22Задача 3
Представить число 1 в виде сумм различных аликвотных дробей
А) трех
слагаемых
1=1/2+1/2=1/2+(1/3+1/6)=1/2+1/3+1/6
Б) четырех слагаемых
1=1/2+1/2=1/2+(1/3+1/6)=1/2+1/3+1/6=1/2+1/3+(1/7+1/42)= 1/2+1/3+1/7+1/42
B) 5-и слагаемых
1=1/2+1/2=1/2+(1/3+1/6)=1/2+1/3+1/6=1/2+1/3+(1/7+1/42)=
1/2+1/3+1/7+1/42=1/2+(1/4+1/12) +1/7+1/42=
1/2+1/4+1/12 +1/7+1/42
1=1/2+1/2=1/2+(1/3+1/6)=1/2+1/3+1/6
Б) четырех слагаемых
1=1/2+1/2=1/2+(1/3+1/6)=1/2+1/3+1/6=1/2+1/3+(1/7+1/42)= 1/2+1/3+1/7+1/42
B) 5-и слагаемых
1=1/2+1/2=1/2+(1/3+1/6)=1/2+1/3+1/6=1/2+1/3+(1/7+1/42)=
1/2+1/3+1/7+1/42=1/2+(1/4+1/12) +1/7+1/42=
1/2+1/4+1/12 +1/7+1/42
Слайд 23Задача 4
Найди сумму
1/(10*11)+1/(11*12)+…+1/(98*99)+1/(99*100)=?
Решение
Найти сумму
1/(1*2)+1/(2*3)+…+1/(98*99)+1/(99*100)=99/100
И вычесть из нее сумму
1/(1*2)+1/(2*3)+…+1/(8*9)+1/(9*10)=9/10
99/100-9/10 = (99-90)/100=9/100=0.09
Слайд 24Задача 5
Чтобы узнать год празднования 100летия Российского государственного академического Большого драматического
театра имени Г. А. Товстоногова (Санкт-Петербург) нужно год проведения в Санкт-Петербурге Чемпионата мира по футболу разделить на сумму аликвотных дробей
1/(1*2) +1/(2*3) +1/(3*4) +…+1/(2018*2019) .
Решение
1/(1*2)+1/(2*3)+1/(3*4)+…+1/(2018*2019)=2018/2019
2018 : 2018/2019 = 2019
1/(1*2) +1/(2*3) +1/(3*4) +…+1/(2018*2019) .
Решение
1/(1*2)+1/(2*3)+1/(3*4)+…+1/(2018*2019)=2018/2019
2018 : 2018/2019 = 2019
Слайд 25Заключение
Разложение на три, четыре, пять и т.д. аликвотных дробей можно
произвести, разложив одно из слагаемых на две дроби, следующее слагаемое еще на две аликвотные дроби и т.д.
Разложение на три, четыре, пять и т.д. аликвотных дробей можно произвести, разложив одно из слагаемых на две дроби, следующее слагаемое еще на две аликвотные дроби и т.д.
Разложение на три, четыре, пять и т.д. аликвотных дробей можно произвести, разложив одно из слагаемых на две дроби, следующее слагаемое еще на две аликвотные дроби и т.д.
Слайд 26Заключение
Аликвотные дроби (с числителем 1) долгое время были единственными дробями,
с которыми как-то умел оперировать человек, а правила действий с произвольными дробями разработаны «сравнительно недавно».
В современной математике вместо египетских дробей используются простые и десятичные дроби, однако египетские дроби продолжают изучаться в теории чисел и истории математики.
В современной математике вместо египетских дробей используются простые и десятичные дроби, однако египетские дроби продолжают изучаться в теории чисел и истории математики.