Презентация, доклад по математике на тему: Алгоритм Евклида

Содержание

1. Презентация по математике на тему: Алгоритм Евклида
2. АЛГОРИТМ ЕВКЛИДААлгоритм Евклида - это алгоритм нахождения
3. Вычисление НОД НОД = наибольший общий делитель
4. Однако существует способ нахождения НОД, не требующий
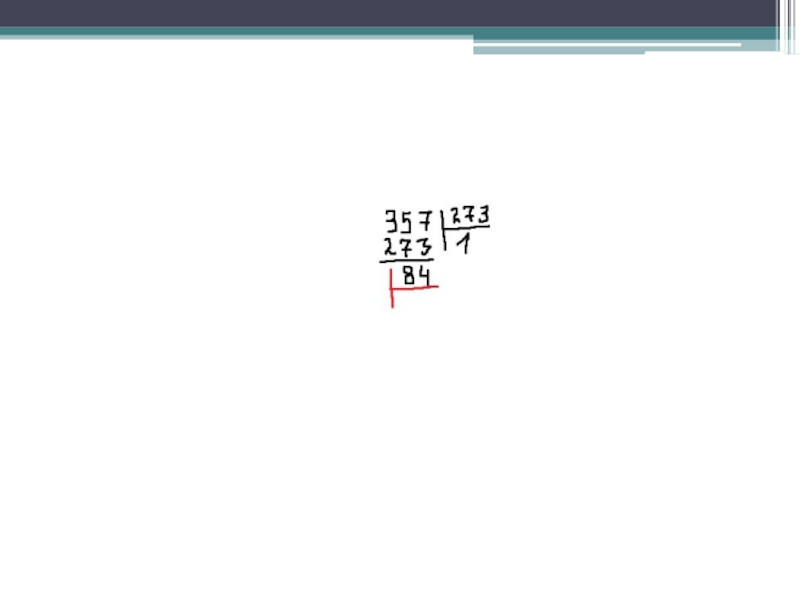
5. Найти НОД (357;273).
6. Слайд 6
7. Слайд 7
8. Слайд 8
9. Слайд 9
10. Слайд 10
11. Слайд 11
12. Слайд 12
13. Слайд 13
14. Слайд 14
15. Слайд 15
16. Слайд 16
17. Слайд 17
18. Слайд 18
19. Слайд 19
20. Слайд 20
21. Слайд 21
22. НОД(357,273) =21
23. Что называется многочленом, одночленом, приведите пример?Что называется степенью многочлена?
24. Пример 2. Найти НОД многочленов Р(х)
25. Слайд 25
26. Слайд 26
27. Слайд 27
28. Слайд 28
29. Слайд 29
30. Слайд 30
31. Слайд 31
32. Слайд 32
33. Слайд 33
34. Слайд 34
35. Слайд 35
36. Слайд 36
37. Слайд 37
38. Слайд 38
39. Слайд 39
40. Слайд 40
41. Слайд 41
42. Слайд 42
43. Слайд 43
44. Слайд 44
45. Слайд 45
46. Слайд 46
47. Слайд 47
48. Слайд 48
49. Слайд 49
50. Слайд 50
51. Слайд 51
52. Слайд 52
53. Слайд 53
54. Слайд 54
55. Слайд 55
56. Слайд 56
57. Таким образом НОД (P,Q)=3х-3
58. Задание по вариантамНайти НОД многочленов:Вариант 1. х4
59. Подведение итогов урокаИтак, на этом уроке вы
60. Домашнее задание:1.Найдите НОД многочленов ((x 6 – 1);(x 8 – 1)) 2.Узнайте, делится ли

АЛГОРИТМ ЕВКЛИДААлгоритм Евклида - это алгоритм нахождения наибольшего общего делителя (НОД) двух целых неотрицательных чисел.Евклид(365-300 до. н. э.)

Главная
Математика
Презентация по математике на тему: Алгоритм Евклида

Слайд 1АЛГОРИТМ ЕВКЛИДА

Слайд 2АЛГОРИТМ ЕВКЛИДА
Алгоритм Евклида - это алгоритм нахождения наибольшего общего делителя (НОД)

двух целых неотрицательных чисел.

Евклид
(365-300 до. н. э.)

Слайд 3Вычисление НОД
НОД = наибольший общий делитель двух натуральных чисел – это

наибольшее число, на которое оба исходных числа делятся без остатка.

НОД(a, b)= НОД(a-b, b)= НОД(a, b-a)

Заменяем большее из двух чисел разностью большего и меньшего до тех пор, пока они не станут равны. Это и есть НОД.

НОД (18, 45) = НОД (18, 45-18) = НОД (18, 27)= НОД (18, 9) = =НОД(9,9)=9

Пример :

Вычисление НОД НОД = наибольший общий делитель двух натуральных чисел – это наибольшее число, на которое оба

Слайд 4Однако существует способ нахождения НОД, не требующий знания всех простых множителей

этих чисел. Этот способ называется алгоритмом Евклида:
большее число делят на меньшее,
затем меньшее на первый остаток,
затем первый остаток – на второй остаток и т.д., пока не получится 0.
Тогда последний остаток – это НОД.