- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Математическая спартакиада.
Содержание
- 1. Презентация по математике Математическая спартакиада.
- 2. Цель мероприятия – пробуждение и развитие
- 3. Слайд 3
- 4. Блез
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. «РАЗМИНКА».
- 9. «ОЛИМПИЙСКИЕ КОЛЬЦА».
- 10. Задача №1: На олимпиаду в Сочи
- 11. Задача
- 12. Задача №3: Олимпийский огонь должен побывать на
- 13. Задача №4: Команда
- 14. Задача №5: Олимпийский
- 15. Черный 528 км/день. Красный: 64 самолетаОранжевый: 329 Желтый: 6400 кмЗеленый: 56,429 метраСиний: 23 м
- 16. «ЕДИНЕНИЕ КОНТИНЕНТОВ». Америка 7649 * 203 =1552747
- 17. Слайд 17
- 18. Олимпийский флаг
- 19. Слайд 19
- 20. «ЭСТАФЕТА».
- 21. Первой команде.1) В тупоугольном треугольнике все углы
- 22. Второй команде.1) Через точку, не лежащую на
- 23. Третьей команде.1) Если угол острый, то смежный
- 24. Слайд 24
- 25. (ок. 580 – ок. 500 г. до н.э.)Пифагор Самосский
- 26. «ГЕОМЕТРИЧЕСКОЕ ЗАДАНИЕ».
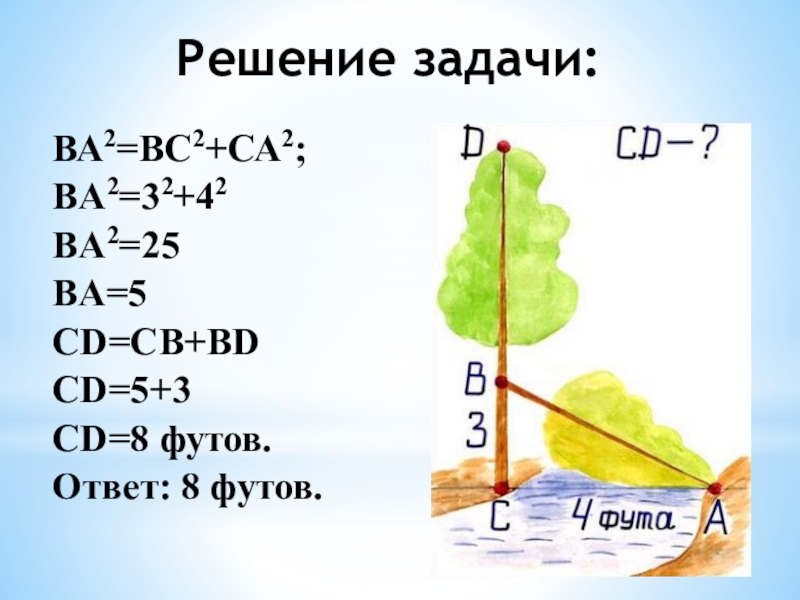
- 27. «На берегу реки рос тополь одинокий.Вдруг ветра
- 28. Решение задачи:ВА2=ВС2+СА2;BA2=32+42BA2=25BA=5CD=CB+BDCD=5+3CD=8 футов.Ответ: 8 футов.
- 29. Слайд 29
- 30. «СОСТЯЗАНИЕ КАПИТАНОВ».
- 31. Карточка №1. В таблице
- 32. Карточка №2. В таблице даны результаты забега
- 33. Карточка №3. В таблице даны результаты
- 34. Слайд 34
- 35. «НАЗВАНИЯ В ДРЕВНОСТИ».
- 36. Как назывались победители Олимпийских
- 37. Слайд 37
- 38. Слайд 38
- 39. Олимпиада
- 40. Слайд 40
- 41. СПАСИБО ЗА ВНИМАНИЕ!
Цель мероприятия – пробуждение и развитие устойчивого познавательного интереса обучающихся к математике и олимпийским играм, используя игровую форму. Задачи: образовательные: - расширить круг знаний учащихся; - раскрыть межпредметную связь математики и
Слайд 2 Цель мероприятия – пробуждение и развитие устойчивого познавательного интереса обучающихся к
математике и олимпийским играм, используя игровую форму.
Задачи:
образовательные:
- расширить круг знаний учащихся;
- раскрыть межпредметную связь математики и физической культуры;
- способствовать выявлению знаний и умений у учащихся в нестандартных ситуациях;
воспитательные:
- воспитание патриотических чувств, гордости за свою страну и россиян;
- воспитание у учащихся инициативности, смекалки;
- развитие умения управлять своим поведением, следовать требованиям коллектива;
развивающие:
- нацелить на сотрудничество и творчество;
- повысить познавательный интерес к математике и здоровому образу жизни;
- учить умению логически мыслить, анализировать и обобщать.
Слайд 4 Блез Паскаль: “Предмет математики столь
серьезен, что не следует упускать ни одной возможности сделать его более занимательным”.
Слайд 10 Задача №1: На олимпиаду в Сочи аккредитовано
14000 представителей прессы
и фотографов.
Сколько самолетов типа ТУ-154 потребуется
для их перевозки, если вместимость
одного самолета 220 человек?
Сколько самолетов типа ТУ-154 потребуется
для их перевозки, если вместимость
одного самолета 220 человек?
Слайд 11 Задача №2: Эстафета олимпийского огня
продлилась 123 дня и была самой протяженной в истории олимпиад – 65 тыс. км. Какова средняя скорость движения факелоносцев? (Ответ округлите до целых.)
Слайд 12Задача №3: Олимпийский огонь должен побывать на космической станции. Средняя высота
полета станции над поверхностью земли 320 км, что составляет 5 % радиуса Земли. Вычислите радиус Земли.
Слайд 13 Задача №4: Команда альпинистов, которая 1 февраля
2014 года поднимала Олимпийский факел на Эльбрус, состояла из ста человек – представителей региональных федераций альпинизма России. Высота горы Эльбрус 5642,9м. Сколько метров нес факел каждый факелоносец?
Слайд 14 Задача №5: Олимпийский факел побывал на дне
самого глубокого озера в мире – Байкала. К середине озера факел доставили на специальном катере «Мангуст». Место погружения находилось неподалеку от истоков реки Ангары. Над водой при помощи специальной установки «прилетел» человек – Жар –птица, который держал в руках символ сочинских игр. Он с помощью летающего ранца Sky Jet (устройство выбрасывает водяные струи) поднялся над поверхностью Байкала и вышел на берег. От него зажгли другой факел, который опустился под воду. Наибольшая глубина озера Байкал 1642м. Олимпийский факел опустили на 1,4 %. На какую глубину был опущен олимпийский факел? (Ответ округлите до целых)
Слайд 15Черный 528 км/день.
Красный: 64 самолета
Оранжевый: 329
Желтый: 6400 км
Зеленый:
56,429 метра
Синий: 23 м
Синий: 23 м
Слайд 16«ЕДИНЕНИЕ КОНТИНЕНТОВ».
Америка 7649 * 203 =1552747
Африка 20134 * 356 =
7167704
Азия 5243 * 128 = 671104
Австралия 1342 * 483 = 648186
Оставшееся кольцо символизирует Европу
Азия 5243 * 128 = 671104
Австралия 1342 * 483 = 648186
Оставшееся кольцо символизирует Европу
Слайд 18 Олимпийский флаг — белое шёлковое полотнище
с вышитыми на нём пятью переплетёнными кольцами голубого, чёрного, красного (верхний ряд), жёлтого и зелёного (нижний ряд) цветов. Идея олимпийского флага проста: пять колец — это пять континентов. Распространена версия, что Европа — синий, Америка — красный, Азия — желтый, Африка — черный, Австралия — зеленый. Пьер де Кубертен говорил, что ни одно из колец не соответствует определённому континенту: шесть цветов (вместе с белым фоном полотна) скомбинированы так, что являют собой национальные цвета всех без исключения стран мира.
Слайд 21Первой команде.
1) В тупоугольном треугольнике все углы тупые. (Нет)
2) В любом
параллелограмме диагонали точкой пересечения делятся пополам. (Да)
3) Диагонали любого прямоугольника равны. (Да)
4) Если точка не лежит на биссектрисе угла, то она равноудалена от сторон этого угла. (Нет)
5) Если в треугольнике есть один острый угол, то этот треугольник остроугольный. (Нет)
3) Диагонали любого прямоугольника равны. (Да)
4) Если точка не лежит на биссектрисе угла, то она равноудалена от сторон этого угла. (Нет)
5) Если в треугольнике есть один острый угол, то этот треугольник остроугольный. (Нет)
Слайд 22Второй команде.
1) Через точку, не лежащую на данной прямой, можно провести
прямую, параллельную этой прямой. (Да)
2) Треугольник со сторонами 1, 2, 4 существует. (Нет)
3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат. (Да)
4) Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла. (Да)
5) Диагонали любого прямоугольника не равны. (Нет)
2) Треугольник со сторонами 1, 2, 4 существует. (Нет)
3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат. (Да)
4) Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла. (Да)
5) Диагонали любого прямоугольника не равны. (Нет)
Слайд 23Третьей команде.
1) Если угол острый, то смежный с ним угол также
является острым. (Нет)
2) Диагонали квадрата взаимно перпендикулярны. (Да)
3) В плоскости все точки, равноудалённые от заданной точки, не лежат на одной окружности. (Нет)
4) Параллелограмм у которого все стороны равны является ромбом. (Да)
5) Любой прямоугольник можно вписать в окружность. (Да)
2) Диагонали квадрата взаимно перпендикулярны. (Да)
3) В плоскости все точки, равноудалённые от заданной точки, не лежат на одной окружности. (Нет)
4) Параллелограмм у которого все стороны равны является ромбом. (Да)
5) Любой прямоугольник можно вписать в окружность. (Да)
Слайд 27
«На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный
тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
Слайд 31 Карточка №1. В таблице даны результаты забега мальчиков
9-го класса на дистанцию 60 м.
Зачёт выставляется, если показано время не хуже 9,8 с. Выпишите номера дорожек, по которым бежали мальчики, получившие зачёт.
Ответ: 2,4
Зачёт выставляется, если показано время не хуже 9,8 с. Выпишите номера дорожек, по которым бежали мальчики, получившие зачёт.
Ответ: 2,4
Слайд 32 Карточка №2. В таблице даны результаты забега мальчиков 5-го класса на
дистанцию 30 м.
Зачёт выставляется, если показано время не хуже 5,9 с. Выпишите номера дорожек, по которым бежали мальчики, получившие зачёт.
Ответ: 2,4
Зачёт выставляется, если показано время не хуже 5,9 с. Выпишите номера дорожек, по которым бежали мальчики, получившие зачёт.
Ответ: 2,4
Слайд 33 Карточка №3. В таблице даны результаты забега мальчиков 8-го класса
на дистанцию 60 м.
Зачёт выставляется, если показано время не хуже 10,5 с. Выпишите номера дорожек, по которым бежали мальчики, получившие зачёт.
Ответ: 1,4
Зачёт выставляется, если показано время не хуже 10,5 с. Выпишите номера дорожек, по которым бежали мальчики, получившие зачёт.
Ответ: 1,4
Слайд 36 Как назывались победители Олимпийских игр в древности:
5007 *(
11815 : 85 – (4806 – 4715))=
Как назывались судьи и распорядители игр:
6003 * (24396 : 76 – 319 + 26)=
Как назывались судьи и распорядители игр:
6003 * (24396 : 76 – 319 + 26)=