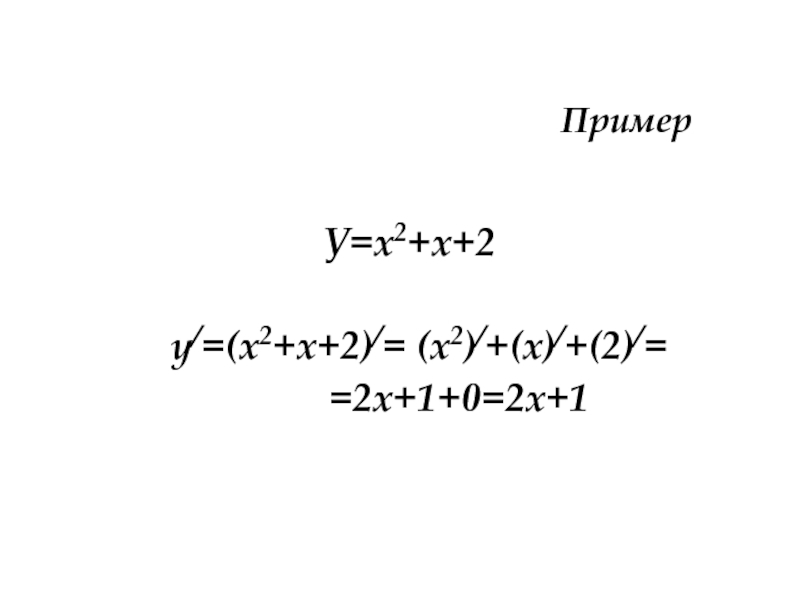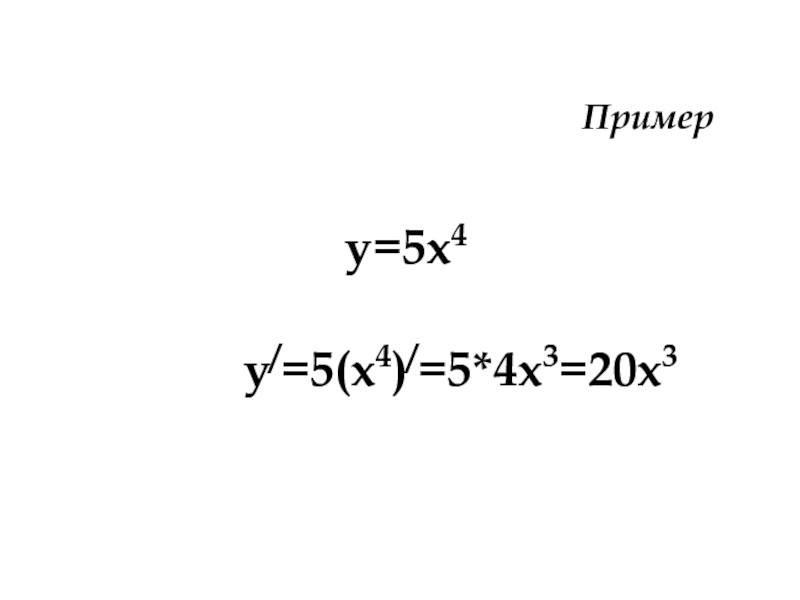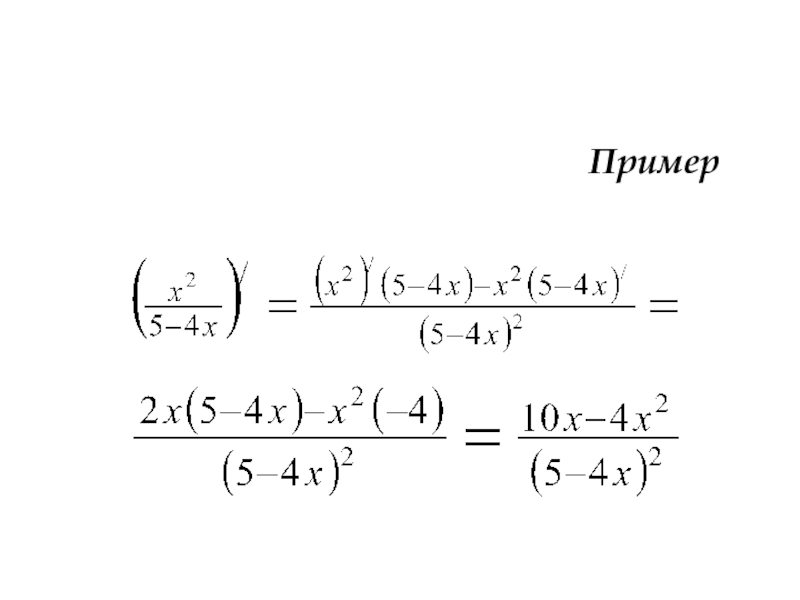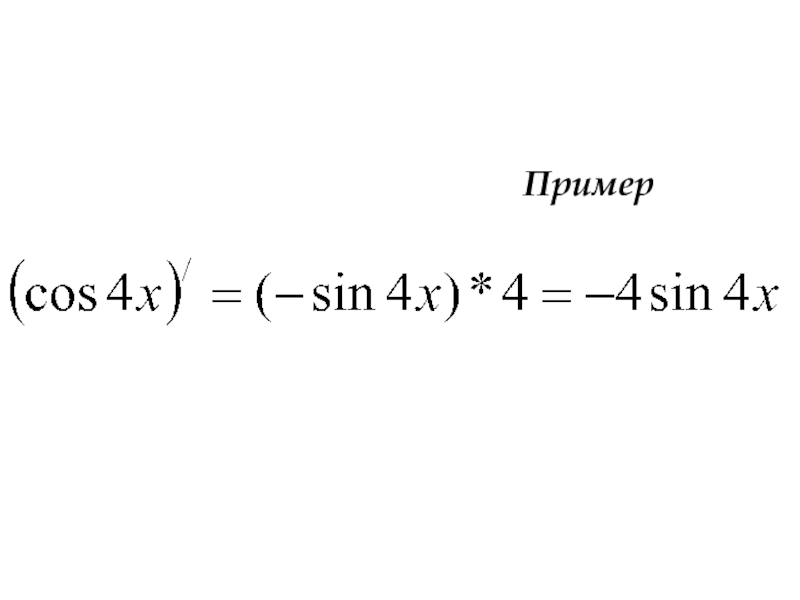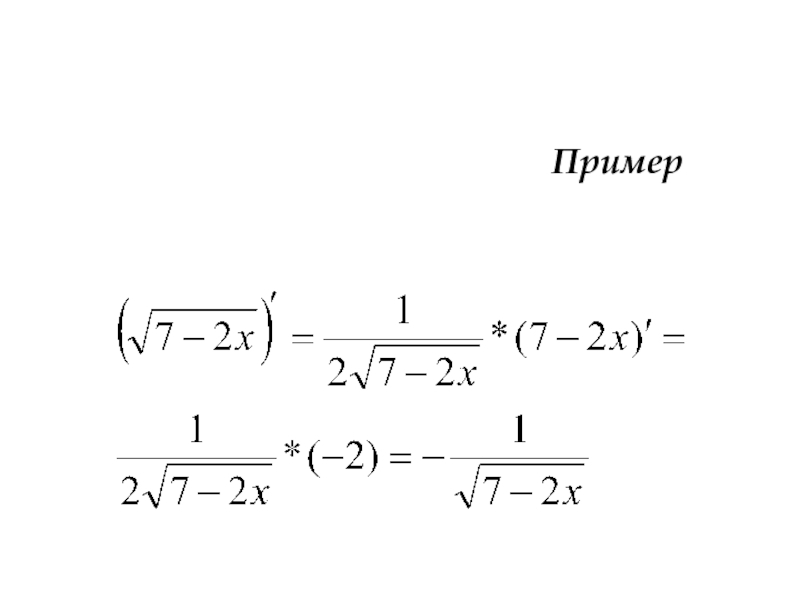- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Интерактивная лекция по теме Производная
Содержание
- 1. Презентация по математике Интерактивная лекция по теме Производная
- 2. Числовой функцией называется соответствие (зависимость), при котором
- 3. 1. Функция , т.к. каждому значению переменной
- 4. График функции Графиком функции f называют
- 5. Касательная к кривой= tg ααα – угол
- 6. Слайд 6
- 7. Слайд 7
- 8. Выражение вида f появилось уже
- 9. Механический смысл производной «Когда величина является максимальной
- 10. Раздел математики, в котором изучаются производные и
- 11. «…нет ни одной области в математике, которая
- 12. Производная в физике Механический смысл производной
- 13. Задача Пусть
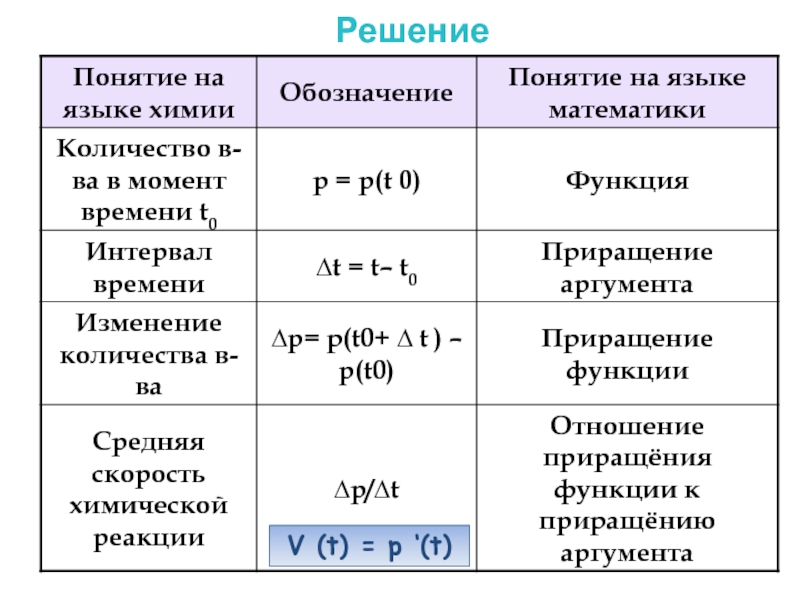
- 14. V (t) = p ‘(t)Решение
- 15. Задача По известной зависимости численности популяции
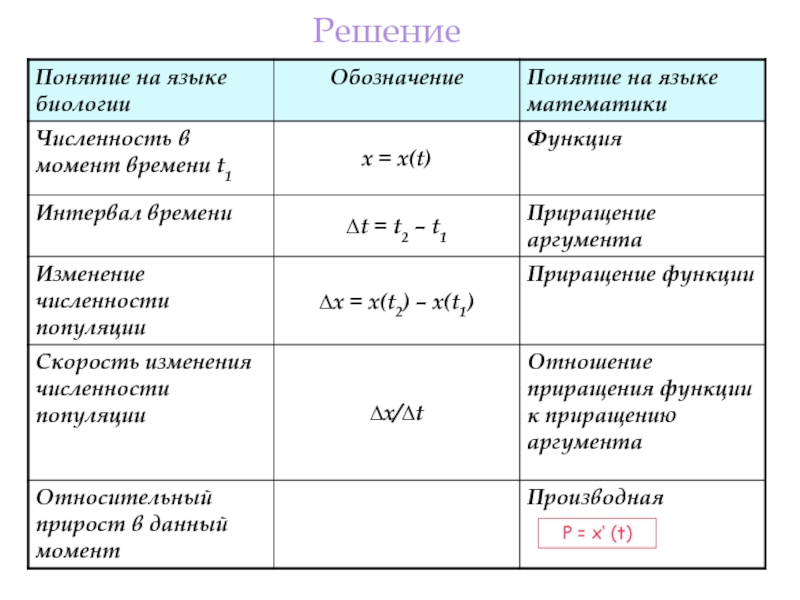
- 16. РешениеР = х‘ (t)
- 17. Задача Вывести формулу для вычисления численности населения на ограниченной территории в момент времени t.Производная в географии
- 18. Решение Пусть у=у(t)- численность населения.Рассмотрим прирост
- 19. Правила дифференцирования
- 20. Производная суммы равна
- 21. Постоянный множитель можно вынести за знак производной
- 22. Производная произведения
- 23. Производная частного
- 24. Пример У=х2+х+2 у/=(х2+х+2)/= (х2)/+(х)/+(2)/= =2х+1+0=2х+1
- 25. Пример у=5х4 у/=5(х4)/=5*4х3=20х3
- 26. Пример У=(2х+3)sinхУ/=((2х+3)sinх)/= (2х+3)/ sinх + (2х+3)( sinх)/=
- 27. Пример
- 28. Производная сложной функции
- 29. Пример
- 30. Пример
- 31. Пример
- 32. Проверь себя!!!Выполните самостоятельную работу
- 33. Найдите производную функции
- 34. Каким вопросам было посвящено занятие?Чему научились на занятии?Какие теоретические факты обобщались на уроке?Подведение итогов урока
- 35. Дальнейшихуспехов в достижении поставленной цели !!!
Слайд 2
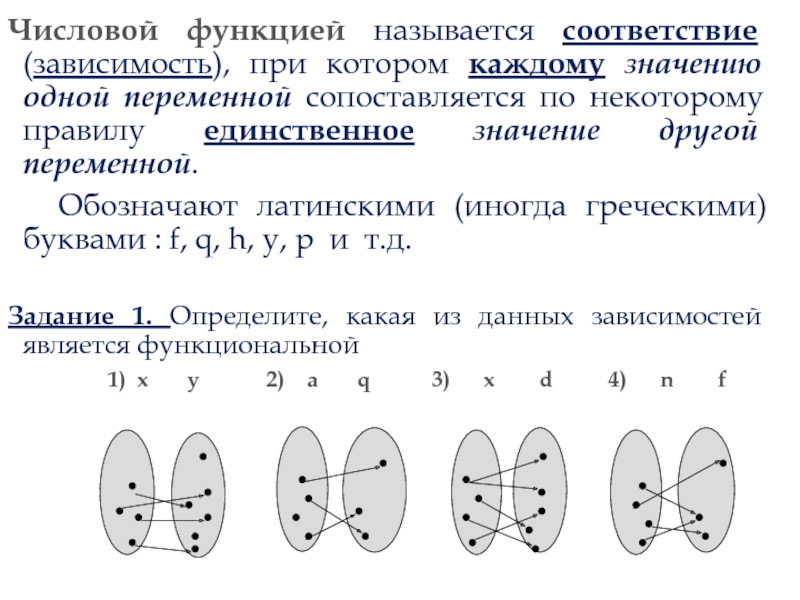
Числовой функцией называется соответствие (зависимость), при котором каждому значению одной переменной
Обозначают латинскими (иногда греческими) буквами : f, q, h, y, p и т.д.
Задание 1. Определите, какая из данных зависимостей является функциональной
1) x y 2) a q 3) x d 4) n f
Слайд 3
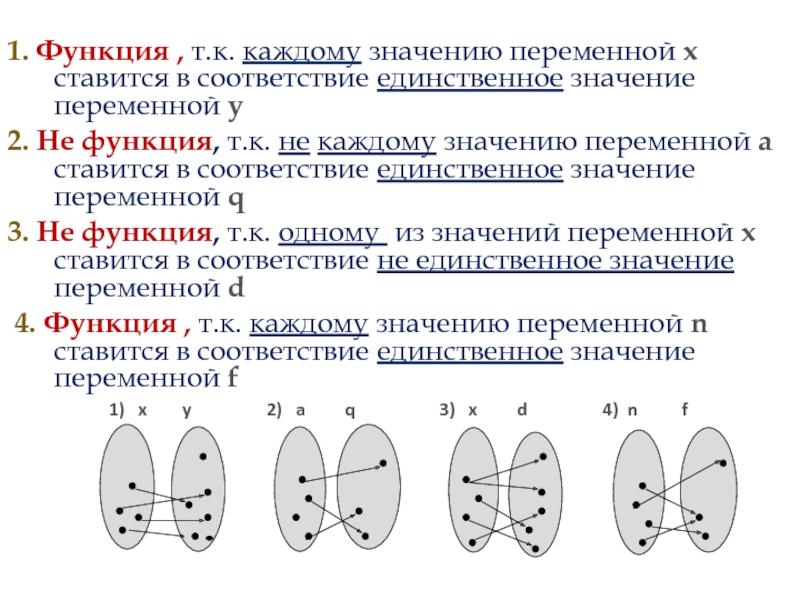
1. Функция , т.к. каждому значению переменной х ставится в соответствие
2. Не функция, т.к. не каждому значению переменной а ставится в соответствие единственное значение переменной q
3. Не функция, т.к. одному из значений переменной х ставится в соответствие не единственное значение переменной d
4. Функция , т.к. каждому значению переменной n ставится в соответствие единственное значение переменной f
1) x y 2) a q 3) x d 4) n f
Слайд 4График функции
Графиком функции f называют множество всех точек (х;
Задание 2. Определите, какой из данных графиков является графиком функции
Рис.1 Рис.2 Рис.3 Рис.4
у
у
у
у
х
х
х
х
НЕ ЯВЛЯЮТСЯ графиками функций рис.1, рис. 3,рис. 4
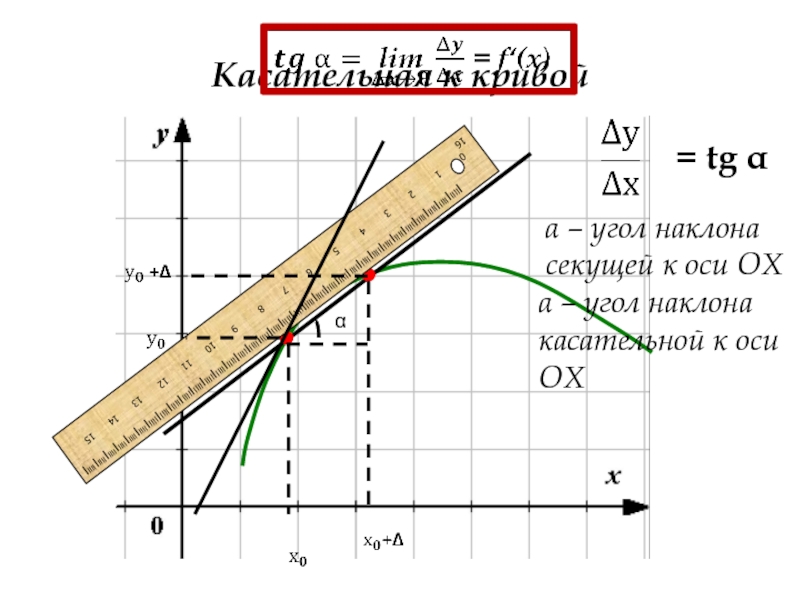
Слайд 5Касательная к кривой
= tg α
α
α – угол наклона секущей к оси
α – угол наклона касательной к оси ОХ
Слайд 8 Выражение вида f появилось уже в конце 17 в.
Термин производная ввел в 1797г. Ж. Лагранж
И. Ньютон называл производную функцию флюксией , а саму функцию – флюентой.
Историческая страничка
1736-1813гг.
1643-1727гг.
Слайд 9Механический смысл производной
«Когда величина является максимальной или минимальной, в этот
Исаак Ньютон (1643 – 1727)
Слайд 10Раздел математики, в котором изучаются производные и их применения к исследованию
Дифференциальное исчисление создано Ньютоном и Лейбницем
в конце 17 столетия.
1646-1716гг.
Слайд 11«…нет ни одной области в математике, которая когда-либо не окажется применимой
Н.И. Лобачевский
Слайд 13Задача
Пусть количество вещества, вступившего в
р(t) = t2/2 + 3t –3 (моль)
Найти скорость химической реакции через 3 секунды.
Производная в химии
Слайд 15Задача
По известной зависимости численности популяции x (t) определить относительный
Производная в биологии
Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.
Слайд 17Задача
Вывести формулу для вычисления численности населения на ограниченной территории в
Производная в географии
Слайд 18Решение
Пусть у=у(t)- численность населения.
Рассмотрим прирост населения за t=t-t0
y=k y
кс – коэффициент смертности)
y/ t=k y
При t0 получим lim y/ t=у’
у’=к у
Слайд 34Каким вопросам было посвящено занятие?
Чему научились на занятии?
Какие теоретические факты обобщались
Подведение итогов урока