стихи С. Погорельского
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Графы и их применение при решении задач (6 класс)
Содержание
- 1. Презентация по математике Графы и их применение при решении задач (6 класс)
- 2. Графы и их применение при решении задачУчитель
- 3. Что такое граф?Графом называют схему, состоящую из
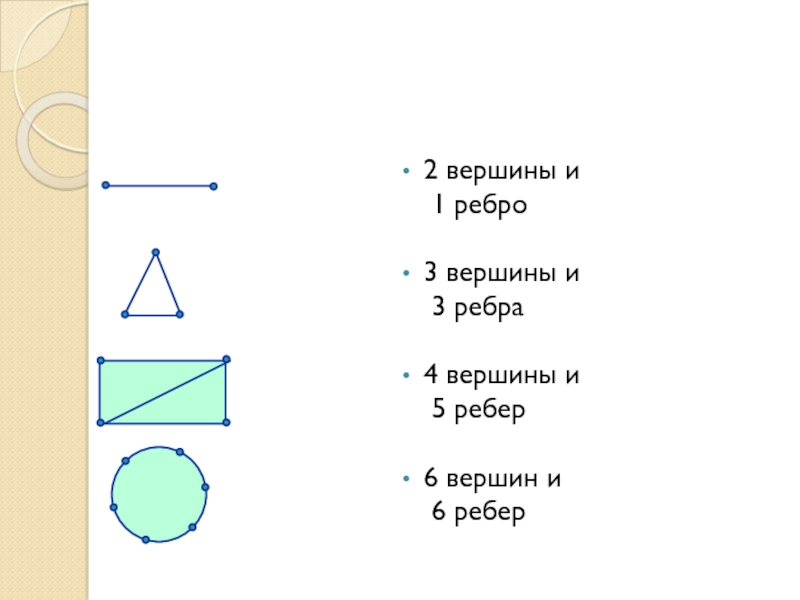
- 4. 2 вершины и 1 ребро3 вершины и 3 ребра4 вершины и 5 ребер6 вершин и 6 ребер
- 5. Число ребер, выходящих из вершины графа,
- 6. Попробуйте начертить каждую из предложенных фигур, не
- 7. Какие буквы русского алфавита можно нарисовать одним
- 8. Задача о Кенигсбергских мостахБывший Кенигсберг (ныне Калининград)
- 9. Задача о Кенигсбергских мостахКенигсбергцы предлагали приезжим следующую
- 10. Задача о Кенигсбергских мостахПройти по Кенигсбергским мостам,
- 11. Задача о Кенигсбергских мостахНо, поскольку граф на
- 12. Одним росчеркомГраф, который можно нарисовать, не отрывая
- 13. Художник-авангардист нарисовал картину "Контур квадрата и его
- 14. Одним росчеркомГраф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком». ?
- 15. Можно ли нарисовать эту картинку, не отрывая
- 16. Задачи Алеша, Боря и Витя учатся в одном
- 17. В компании из семи мальчиков каждый имеет
- 18. Между 9 планетами Солнечной системы введено космическое
- 19. «Если задуманное число умножить на 5 и
- 20. Слайд 20
- 21. Машина ехала 3 часа со скоростью 65
- 22. Слайд 22
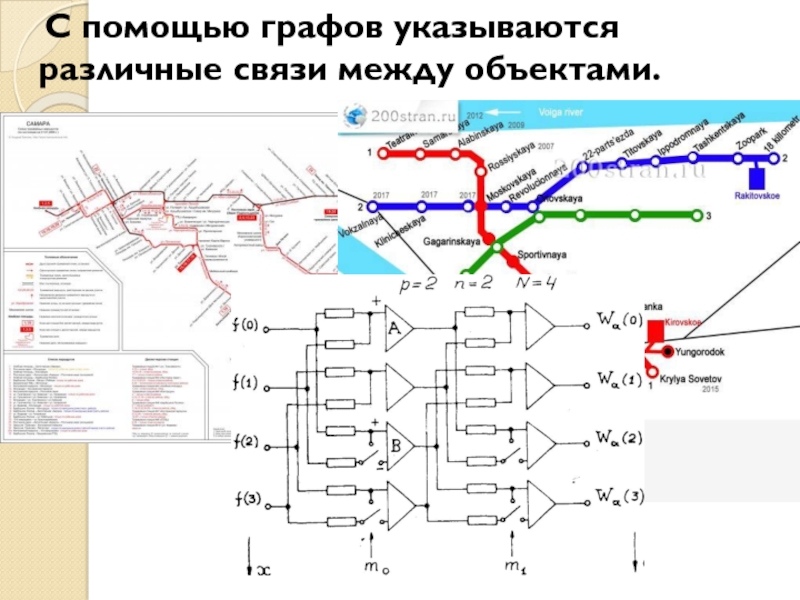
- 23. С помощью графов указываются различные связи между объектами.
- 24. Инженер чертит схемы электрических цепей.Химик рисует структурные
- 25. (География 10 кл. В.П. Максаковский)
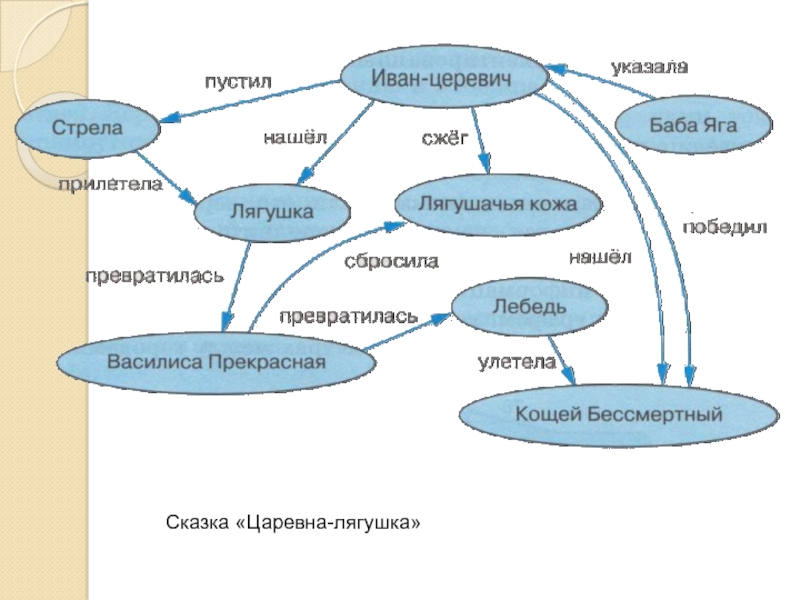
- 26. Сказка «Царевна-лягушка»
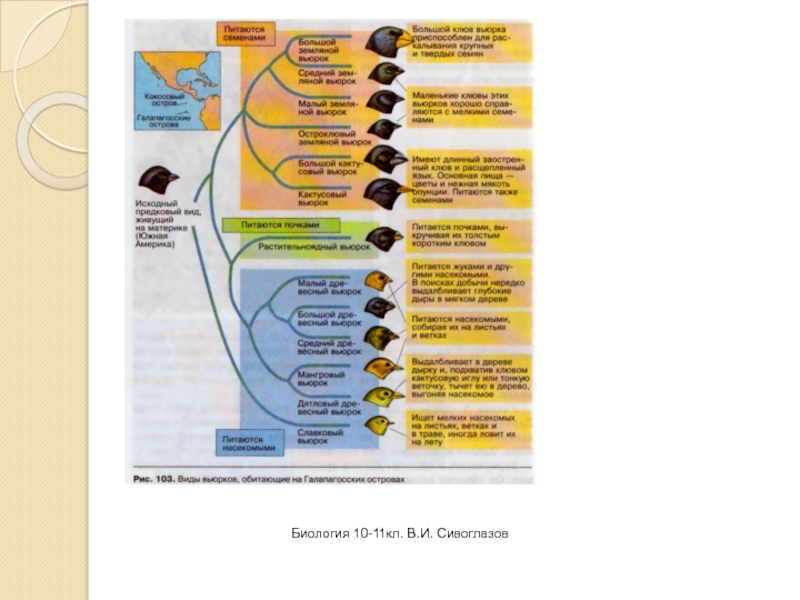
- 27. Биология 10-11кл. В.И. Сивоглазов
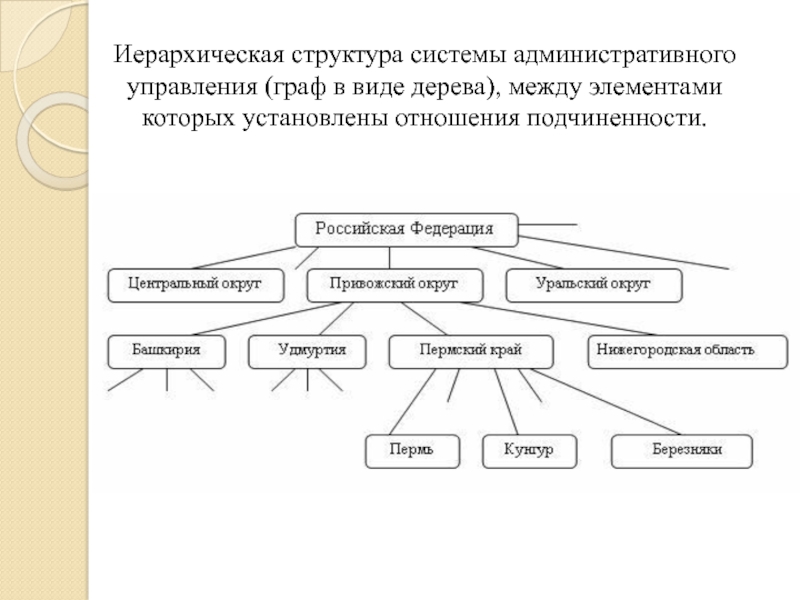
- 28. Иерархическая структура системы административного управления (граф в виде дерева), между элементами которых установлены отношения подчиненности.
- 29. Изучение графов позволяет:Развивать интерес к предмету математика.Сформировать
- 30. Спасибо за внимание!!!!
Графы и их применение при решении задачУчитель математики МБОУ СОШ № 121 г. о. СамараМусалимова Людмила Петровна
Слайд 1 В столярке работает четверо нас: Беляев, Гуляев, Анютка, Тарас. Вот как-то профорг заглянул
на минутку:
- Кто ходит на лыжах?
- Тарас и Анютка.
- Кто плавать умеет?
- Анютка, Тарас.
- Кто в теннис играет?
- Они же, как раз.
- Есть шахматисты?
- Беляев, Гуляев.
- Мотоциклисты?
- Беляев, Гуляев.
- Бывал ли в походе кто-либо из вас?
- Беляев, Гуляев, Анютка, Тарас.
Устроили наши ответы профорга,
Он все записал, не скрывая восторга.
А вскоре весьма и весьма озадачены,
Читали в стенновке мы рапорт такой:
«Пятнадцатью видами спорта охвачены
Все сорок рабочих у нас в мастерской!»
Слайд 2Графы и их применение при решении задач
Учитель математики МБОУ СОШ №
121 г. о. Самара
Мусалимова Людмила Петровна
Мусалимова Людмила Петровна
Слайд 3Что такое граф?
Графом называют схему, состоящую из точек (вершины графа) и
соединяющих эти точки отрезков, прямых или кривых (ребра графов)
Рёбра графа
Вершины графа
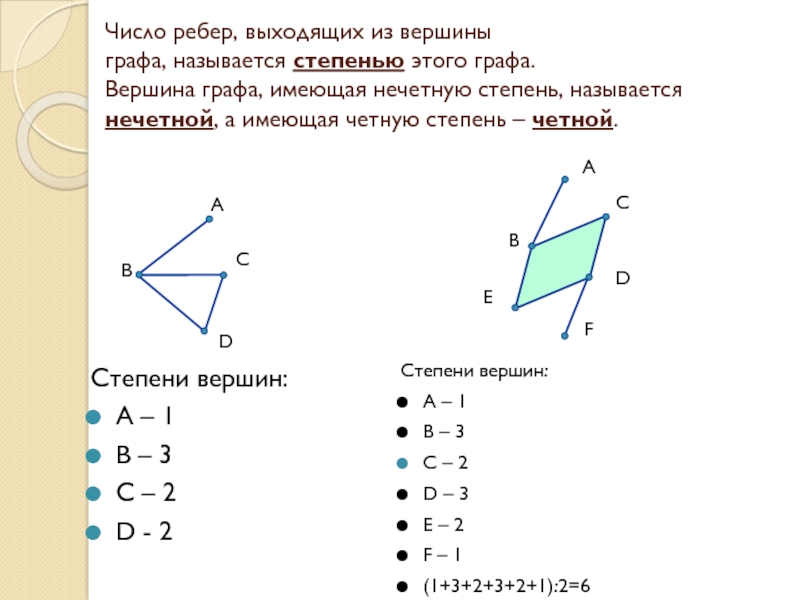
Слайд 5Число ребер, выходящих из вершины графа, называется степенью этого графа. Вершина графа,
имеющая нечетную степень, называется нечетной, а имеющая четную степень – четной.
Степени вершин:
А – 1
В – 3
С – 2
D - 2
Степени вершин:
А – 1
В – 3
С – 2
D – 3
E – 2
F – 1
(1+3+2+3+2+1):2=6
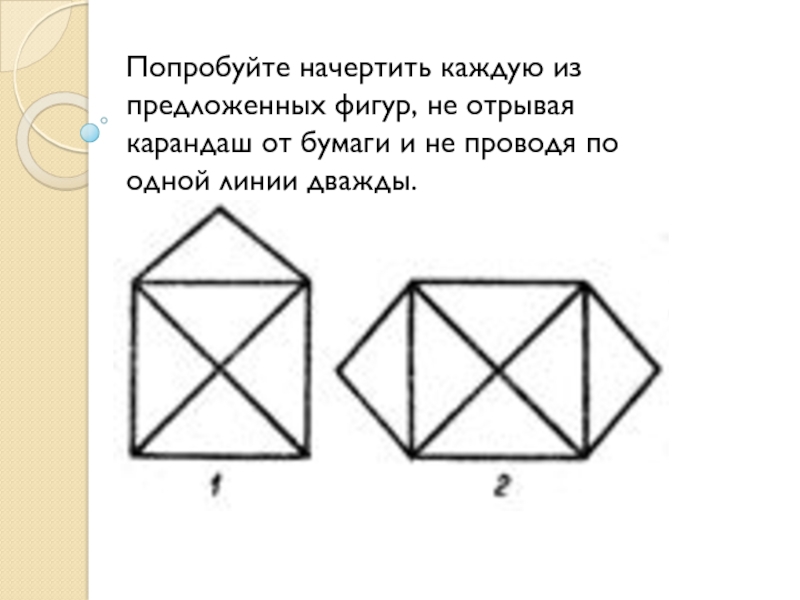
Слайд 6Попробуйте начертить каждую из предложенных фигур, не отрывая карандаш от бумаги
и не проводя по одной линии дважды.
Слайд 7Какие буквы русского алфавита можно нарисовать одним росчерком?
Б, В, Г, З,
И, Л, М, О, П, Р, С, Ф, Ъ, Ь, Я.
Слайд 8Задача о Кенигсбергских мостах
Бывший Кенигсберг (ныне Калининград) расположен на реке Прегель.
В пределах города река омывает два острова. С берегов на острова были перекинуты мосты. Старые мосты не сохранились, но осталась карта города, где они изображены.
Слайд 9Задача о Кенигсбергских мостах
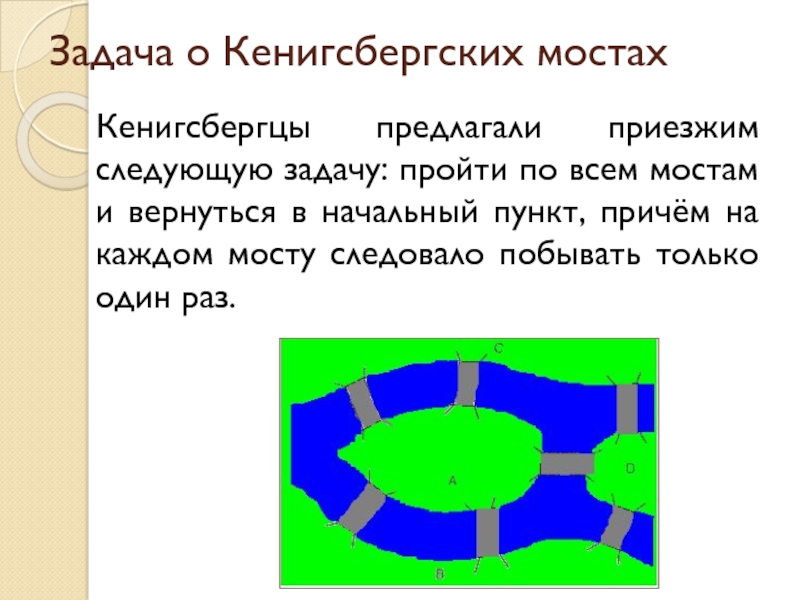
Кенигсбергцы предлагали приезжим следующую задачу: пройти по всем
мостам и вернуться в начальный пункт, причём на каждом мосту следовало побывать только один раз.
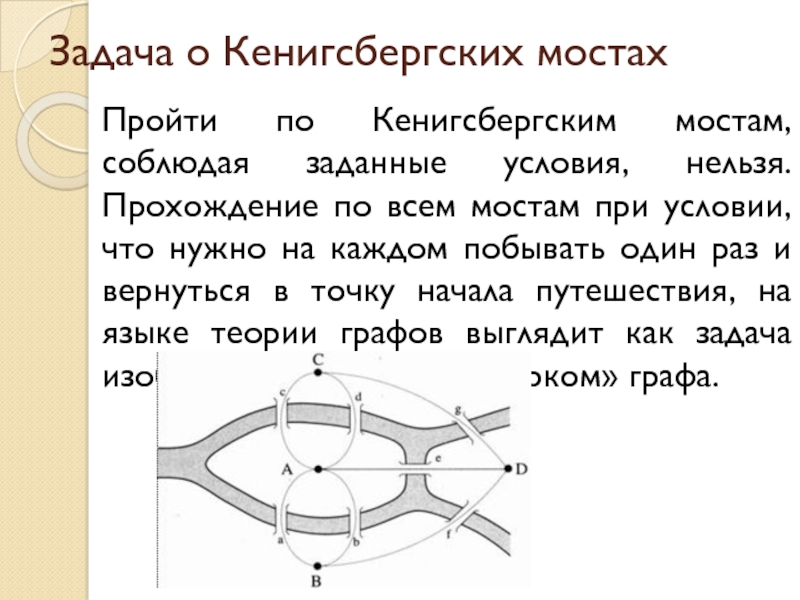
Слайд 10Задача о Кенигсбергских мостах
Пройти по Кенигсбергским мостам, соблюдая заданные условия, нельзя.
Прохождение по всем мостам при условии, что нужно на каждом побывать один раз и вернуться в точку начала путешествия, на языке теории графов выглядит как задача изображения «одним росчерком» графа.
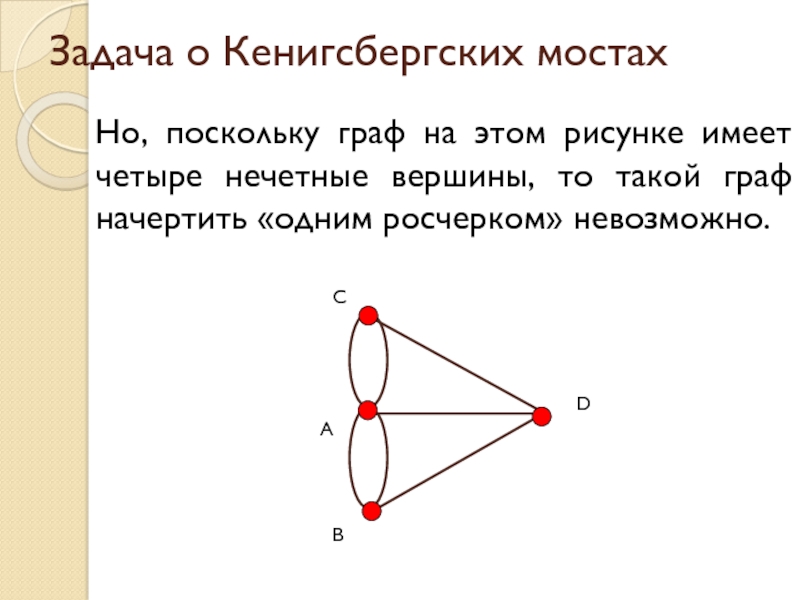
Слайд 11Задача о Кенигсбергских мостах
Но, поскольку граф на этом рисунке имеет четыре
нечетные вершины, то такой граф начертить «одним росчерком» невозможно.
С
В
D
A
Слайд 12Одним росчерком
Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется
эйлеровым.
Решая задачу О кенигсбергских мостах, Эйлер сформулировал свойства графа:
Невозможно начертить граф с нечетным числом нечетных вершин.
Решая задачу О кенигсбергских мостах, Эйлер сформулировал свойства графа:
Невозможно начертить граф с нечетным числом нечетных вершин.
Слайд 13Художник-авангардист нарисовал картину "Контур квадрата и его диагонали". Мог ли он
нарисовать свою картину не отрывая карандаша от бумаги и не проводя одну линию дважды?
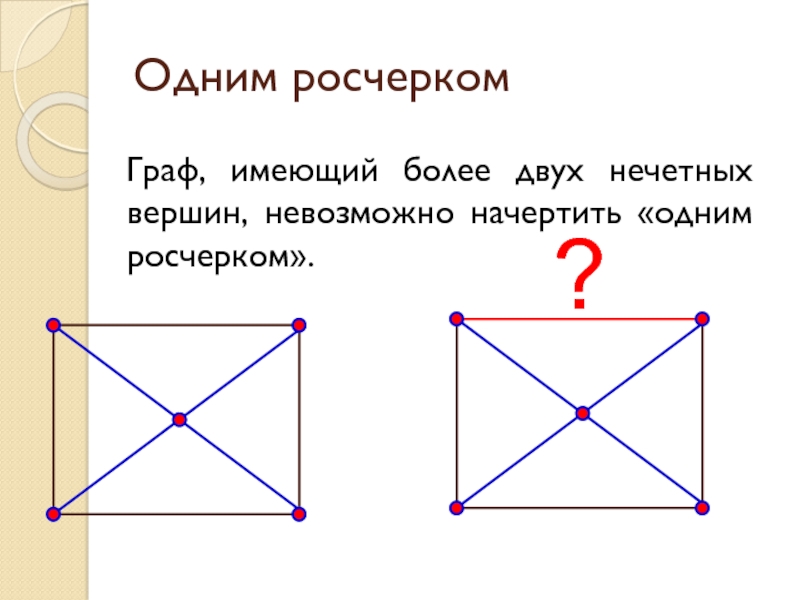
Слайд 14Одним росчерком
Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком».
?
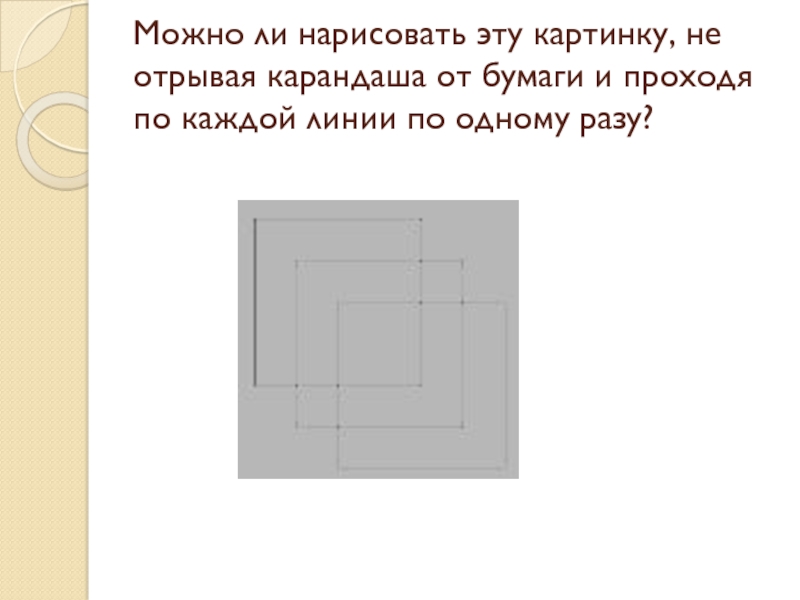
Слайд 15Можно ли нарисовать эту картинку, не отрывая карандаша от бумаги и
проходя по каждой линии по одному разу?
Слайд 16Задачи
Алеша, Боря и Витя учатся в одном классе. Один ездит домой
из школы на автобусе, другой – на трамвае, третий – на троллейбусе. Однажды после уроков Алеша пошел проводить друга до остановки автобуса. Когда мимо них проходил троллейбус, третий друг крикнул из окна: «Боря, ты забыл в школе тетрадь!» Кто на чем ездит домой?
Слайд 17В компании из семи мальчиков каждый имеет среди остальных не менее
трёх братьев. Докажите, что все семеро – братья.
Слайд 18 Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают по
следующим маршрутам: Земля-Меркурий, Плутон-Венера, Земля-Плутон, Плутон-Меркурий, Меркурий-Венера, Уран-Нептун, Нептун-Сатурн, Сатурн-Юпитер, Юпитер-Марс и Марс-Уран. Можно ли добраться с Земли до Марса?
Слайд 19 «Если задуманное число умножить на 5 и к полученному результату прибавить
1, потом полученную сумму умножить на 7 и полученное произведение увеличить на 4, то получим число, которое в 16 раз больше числа 135. Найдите задуманное число».
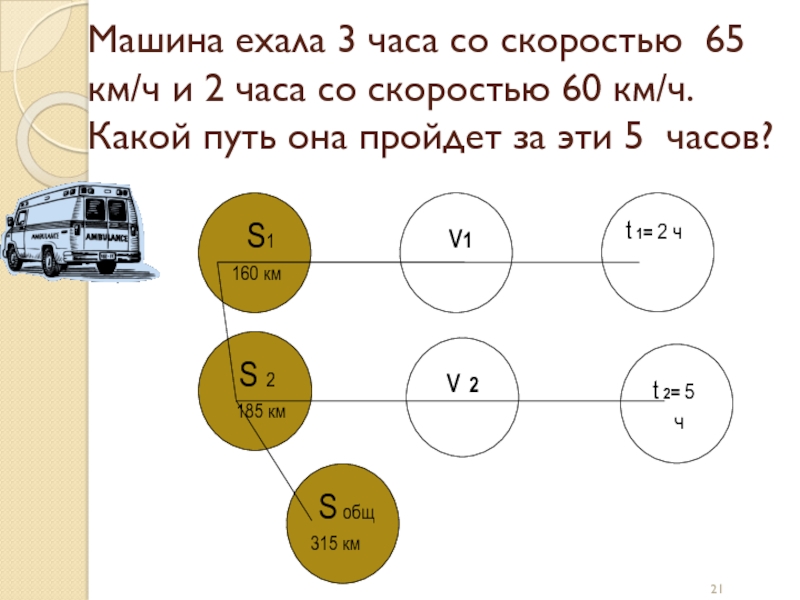
Слайд 21Машина ехала 3 часа со скоростью 65 км/ч и 2 часа
со скоростью 60 км/ч.
Какой путь она пройдет за эти 5 часов?
S1
160 км
t 1= 2 ч
S 2
185 км
v 2
t 2= 5 ч
v1
S общ
315 км
Слайд 24Инженер чертит схемы электрических цепей.
Химик рисует структурные формулы, чтобы показать, как
в сложной молекуле с помощью валентных связей соединяются друг с другом атомы.
Историк прослеживает родословные связи по генеалогическому дереву.
Военачальник наносит на карту сеть коммуникаций, по которым из тыла к передовым частям доставляется подкрепление.
Социолог по сложнейшей диаграмме показывает, как подчиняются друг другу различные отделы одной огромной корпораций.
Историк прослеживает родословные связи по генеалогическому дереву.
Военачальник наносит на карту сеть коммуникаций, по которым из тыла к передовым частям доставляется подкрепление.
Социолог по сложнейшей диаграмме показывает, как подчиняются друг другу различные отделы одной огромной корпораций.
Слайд 28Иерархическая структура системы административного управления (граф в виде дерева), между элементами
которых установлены отношения подчиненности.
Слайд 29Изучение графов позволяет:
Развивать интерес к предмету математика.
Сформировать представление о значении теории
графов как средства описания действительности
Развивать логическое мышление, умение анализировать при решении задач.
Применять элнменты теории графов в других предметах.
Развивать логическое мышление, умение анализировать при решении задач.
Применять элнменты теории графов в других предметах.