- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Функции вокруг нас или мы в мире функций.
Содержание
- 1. Презентация по математике Функции вокруг нас или мы в мире функций.
- 2. Теория без практики мертва или бесплодна: практика
- 3. Математика – одна из древнейших наук. За
- 4. Они внесли особый вклад в развитие математики!Л.В.
- 5. Функция – одно из основных общенаучных понятий;
- 6. Периодические процессыВ природе и технике часто встречаются
- 7. Показательная функция в наукеВ биологии есть законы,
- 8. Рост различных видов микроорганизмов и бактерий, дрожжей,
- 9. Закон органического затухания: подобен размножению,
- 10. В физике тоже есть величины и законы
- 11. Также широко применяется показательная функция при описании
- 12. При прохождении света через мутную среду каждый
- 13. Широкое применение нашла логарифмическая функция в астрономии:
- 14. Понятие логарифмической спирали: Логарифмическая спираль – это
- 15. Если взглянуть на форму многих галактик, то
- 16. Логарифмическая спираль нередко используется в технических устройствах.
- 17. Слайд 17
- 18. Логарифмическая спираль в природе
- 19. Раковины морских животных могут расти лишь в
- 20. Рога таких млекопитающих как архары (горные козлы),
- 21. Один из наиболее распространенных пауков ЭПЕЙРА, сплетая
- 22. Пушки и ученые.Траекториями метательных снарядов интересовался знаменитый философ древности Аристотель.
- 23. В ХII веке н.э монах Бертольд Шварц
- 24. Первым из математиков решал эту задачу в
- 25. Размышляя над движением артиллерийских снарядов,Тарталья пришел к
- 26. «Сближение теории с практикой дает самые благотворные
- 27. Основная область применения производной функций - задачи на оптимизацию!
- 28. "Наибольший" стакан и "наибольшая" консервная банка rhЧтобы
- 29. Не только люди стремятся оптимизировать свой труд.Например,
Слайд 2Теория без практики мертва или бесплодна: практика без теории невозможна или
Для теории нужны знания, для практики сверх всего того, - и умения
А. Н. Крылов
Слайд 3Математика – одна из древнейших наук. За долгую историю своего существования
Чрезвычайно расширились связи математики с другими науками. Теперь она с успехом используется и в таких областях научного знания, о которых ещё недавно думали, что они не допускают внедрения математических методов. Такое мнение существовало о биологии, медицине, языкознании и некоторых отраслях общественных наук.
Возможности использовать математику для решения практических задач промышленности, сельского хозяйства и транспорта ныне представляются неограниченными.
Слайд 4Они внесли особый вклад в развитие математики!
Л.В. Канторович
Выдающийся советский математик, ныне
А.Н. Колмогоров
Герой Социалистического Труда, академик. Создал новую область математики -теорию информации.
А.Н. Крылов
Российский математик, академик Герой Социалистического Труда. Впервые в истории науки сформулировал один из принципов вычислительной культуры.
Слайд 5Функция – одно из основных общенаучных понятий;
оно выражает взаимосвязь между
принадлежит Лейбницу и происходит от латинского слова functio,что означает «выполнение», «осуществление».
Слайд 6Периодические процессы
В природе и технике часто встречаются процессы, которые периодически повторяются
Например, если маятник делает одно полное колебание за Т секунд, то его отклонение от положения равновесия в моменты времени t, t+T, t+2T и т.д. будет одним и тем же.
Периодически с периодом в 1 год меняется расстояние Земли от Солнца.
С периодом в 1 лунный месяц меняются фазы Луны.
Периодически изменяющиеся величины описывают с помощью периодических функций.
Слайд 7Показательная функция в науке
В биологии есть законы, которые можно описать с
показательной функции. Например:
1. Закон органического размножения: при благоприятных условиях
(отсутствие) врагов, большое количество пищи) живые организмы
размножались бы по закону показательной функции.
Например: одна комнатная муха может за лето произвести 8× 1014 особей
потомства. Их вес составил бы несколько миллионов тонн
(а вес потомства пары мух превысил бы вес нашей планеты), они бы заняли огромное
пространство, а если выстроить их в цепочку, то её длинна будет больше,
чем расстояние от Земли до Солнца.
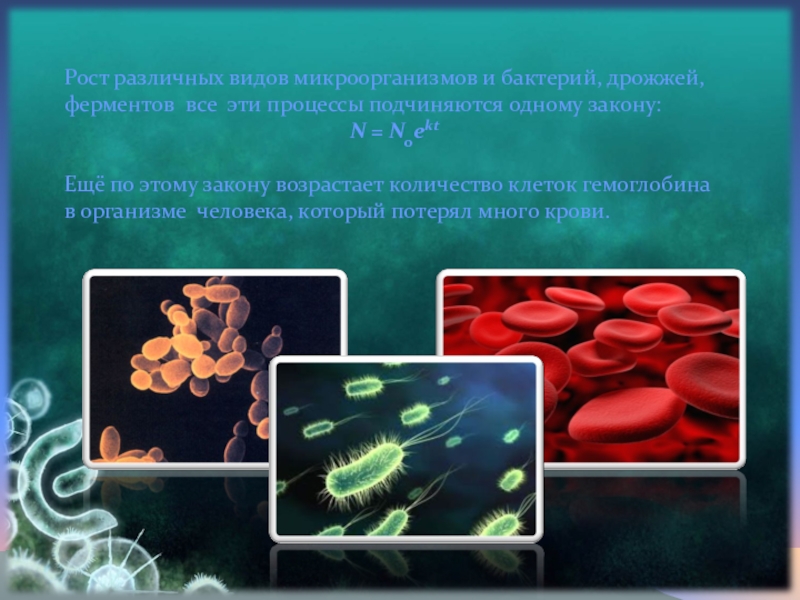
Слайд 8Рост различных видов микроорганизмов и бактерий, дрожжей,
ферментов все эти процессы
Ещё по этому закону возрастает количество клеток гемоглобина
в организме человека, который потерял много крови.
Слайд 9Закон органического затухания: подобен размножению,
происходит с
происходит в обратную сторону.
Закон выравнивания: он тоже описывается показательной
функцией и присутствует при таких процессах, как разрушение
адреналина в крови и уменьшение количества радиоактивных
веществ, выводимых почками.
Слайд 10В физике тоже есть величины и законы
подчиненные показательной функции:
Например процесс
температуры чайника при кипении выражается формулой:
T = T0+ (100 - T0)e-kt - это пример
процесса выравнивания, который
в физике также можно наблюдать
при включении и выключении
электрических цепей, и при
падении тела с парашютом.
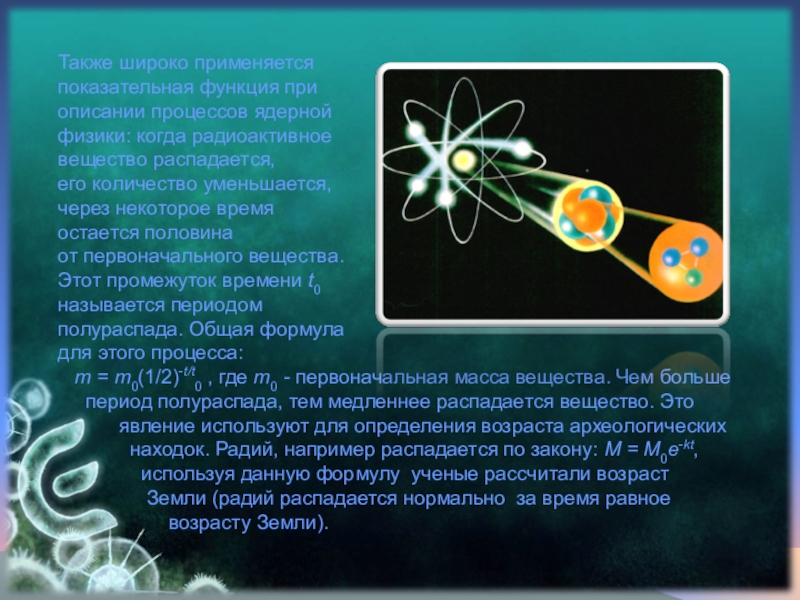
Слайд 11Также широко применяется
показательная функция при
описании процессов ядерной
физики: когда
вещество распадается,
его количество уменьшается,
через некоторое время
остается половина
от первоначального вещества.
Этот промежуток времени t0
называется периодом
полураспада. Общая формула
для этого процесса:
m = m0(1/2)-t/t0 , где m0 - первоначальная масса вещества. Чем больше
период полураспада, тем медленнее распадается вещество. Это
явление используют для определения возраста археологических
находок. Радий, например распадается по закону: M = M0e-kt,
используя данную формулу ученые рассчитали возраст
Земли (радий распадается нормально за время равное
возрасту Земли).
Слайд 12При прохождении света через мутную среду каждый слой этой среды поглощает
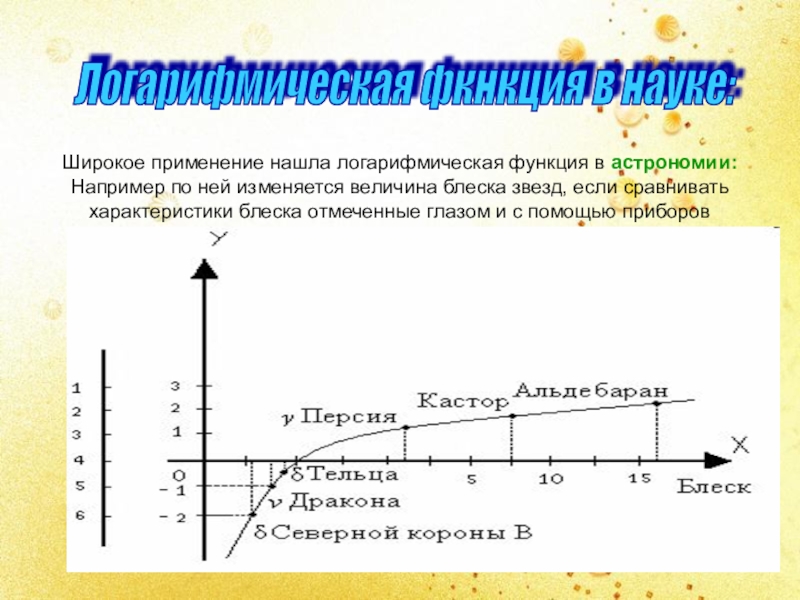
Слайд 13Широкое применение нашла логарифмическая функция в астрономии:
Например по ней изменяется
Логарифмическая фкнкция в науке:
Слайд 14Понятие логарифмической спирали:
Логарифмическая спираль – это линии в геометрии, отличные
Логарифмическую спираль называют равноугольной спиралью. Это её название отражает тот факт, что в любой точке логарифмической спирали угол между касательной к ней и радиус – вектором сохраняет постоянное значение.
Слайд 15Если взглянуть на форму многих галактик, то можно обнаружить, что некоторые
Галактика млечный путь - типичная спиральная галактика.
Слайд 16Логарифмическая спираль нередко используется в технических
устройствах. Например, вращающиеся ножи
нередко
логарифмической спирали
– под постоянным углом к разрезаемой поверхности, благодаря чему лезвие ножа стачивает равномерно.
Слайд 17
Если же он полетит на восток, то, ______ облетев параллель, вернётся в тот же _______ пункт, из которого вылетел.
Предположим теперь, что самолёт будет лететь, пересекая все меридианы под одним и тем же углом, отличным от прямого, т.е. держась всё время одного и того же курса. Когда он облетит земной шар, то попадёт в точку, имеющую ту же долготу, что и точка вылета, но расположенную ближе к Северному полюсу. После следующего облёта он окажется ещё ближе к полюсу и, продолжая лететь указанным образом, будет описывать вокруг полюса сужающуюся спираль.
Слайд 19Раковины морских животных могут расти лишь в одном направлении.
Чтобы не
А такой рост может совершаться лишь по логарифмической спирали.
Можно сказать, что эта спираль является математическим символом соотношения форм роста.
Слайд 20Рога таких млекопитающих как архары (горные козлы), закручены по логарифмической спирали.
Семечки подсолнуха
расположены по дугам, близким к
логарифмической спирали
Слайд 21Один из наиболее распространенных пауков ЭПЕЙРА, сплетая паутину, закручивает нити вокруг
Цепочки молекулы ДНК закручены по логарифмической спирали
Слайд 22Пушки и ученые.
Траекториями метательных снарядов интересовался знаменитый философ древности Аристотель.
Слайд 23В ХII веке н.э монах Бертольд Шварц изобрел порох. Это повлекло революцию
Слайд 24Первым из математиков решал эту задачу в XVI веке гениальный самоучка
Он занимался многими вопросами математики и механики:открыл формулу для решения кубического уравнения,изучил некоторые комбинаторные задачи т.д.
Однако его не признавали университетские ученые,и открытия носили имена других математиков.
Слайд 25Размышляя над движением артиллерийских снарядов,Тарталья пришел к выводу,что снаряд пролетит наибольшее
Слайд 26«Сближение теории с практикой дает самые благотворные результаты, и не одна
П. Л. Чебышев
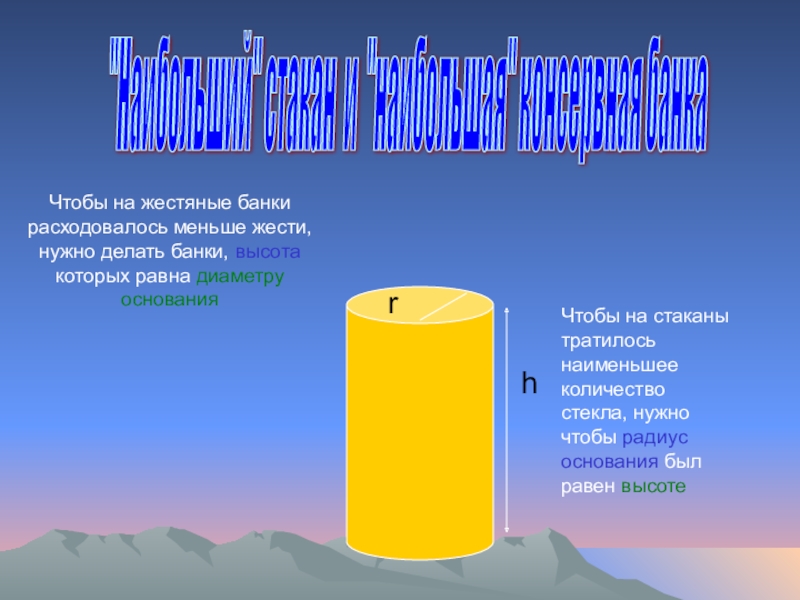
Слайд 28"Наибольший" стакан и "наибольшая" консервная банка
r
h
Чтобы на жестяные банки расходовалось
Чтобы на стаканы тратилось наименьшее количество стекла, нужно чтобы радиус основания был равен высоте
Слайд 29Не только люди стремятся оптимизировать свой труд.
Например, форма ячеек пчелиных сот
что при заданном объёме на них идёт
наименьшее количество воска.
«Но и самый плохой архитектор от наилучшей пчелы с самого начала отличается тем, что прежде чем строить ячейку из воска, он уже построил её в своей голове».
К. Маркс.