- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по предмету Теория вероятностей и математическая статистика Основы математической статистики
Содержание
- 1. Презентация по предмету Теория вероятностей и математическая статистика Основы математической статистики
- 2. Основные понятияВариационный ряд – ряд, в котором сопоставлены
- 3. формы вариационного рядаРазличают три формы вариационного ряда:
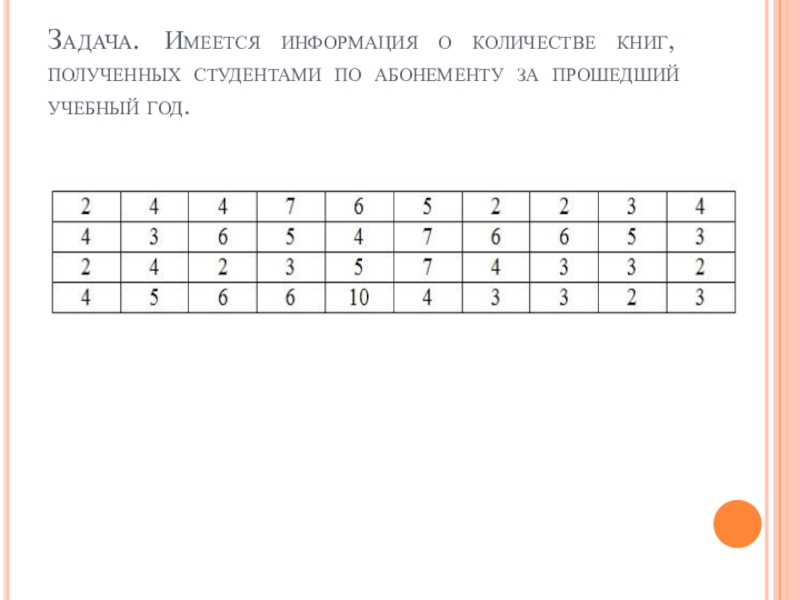
- 4. Задача. Имеется информация о количестве книг, полученных студентами по абонементу за прошедший учебный год.
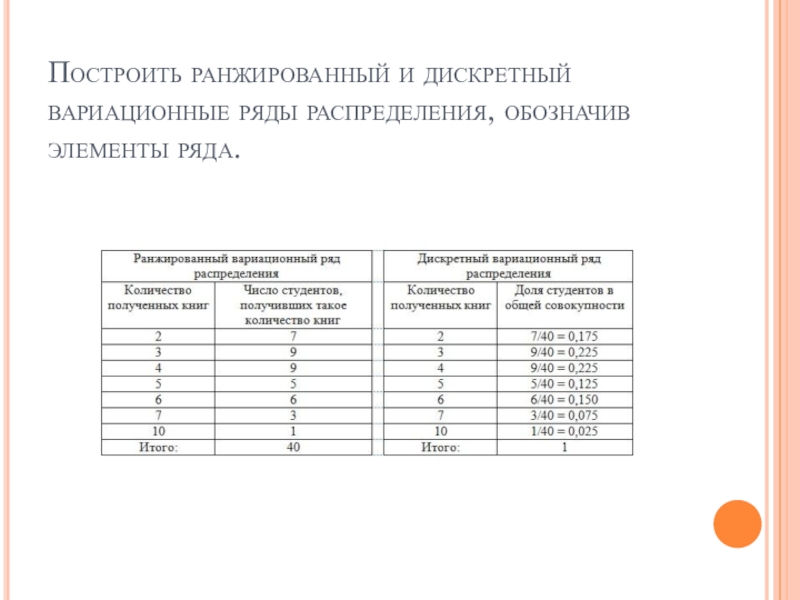
- 5. Построить ранжированный и дискретный вариационные ряды распределения, обозначив элементы ряда.
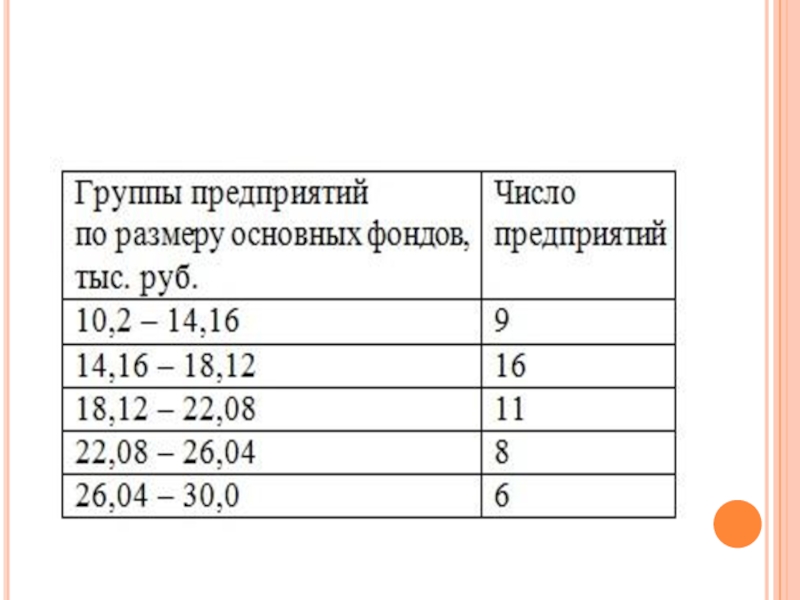
- 6. Задача 2. Имеются данные о стоимости основных фондов у 50 предприятий, тыс. р.
- 7. Построить ряд распределения, выделив 5 групп предприятий
- 8. Слайд 8
- 9. Показатели вариационного рядаСредняя арифметическая - это обобщающий показатель,
- 10. Мода – еще одна средняя величина вариационного ряда,
Основные понятияВариационный ряд – ряд, в котором сопоставлены (по степени возрастания или убывания)варианты и соответствующие им частоты .Варианты – отдельные количественные выражения признака.Частота – число, показывающее, сколько раз повторяется варианта. Частостями называются частоты, выраженные в долях единицы или в процентах к
Слайд 2Основные понятия
Вариационный ряд – ряд, в котором сопоставлены (по степени возрастания или
убывания)варианты и соответствующие им частоты .
Варианты – отдельные количественные выражения признака.
Частота – число, показывающее, сколько раз повторяется варианта.
Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частостей равна 1 или 100%.
Варианты – отдельные количественные выражения признака.
Частота – число, показывающее, сколько раз повторяется варианта.
Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частостей равна 1 или 100%.
Слайд 3формы вариационного ряда
Различают три формы вариационного ряда: ранжированный ряд, дискретный ряд
и интервальный ряд.
Ранжированный вариационный ряд - это распределение отдельных единиц совокупности в порядке возрастания или убывания исследуемого признака.
Дискретный вариационный ряд характеризует распределение единиц совокупности по дискретному признаку, принимающему только целые значения.
Если признак имеет непрерывное изменение, которые в определенных границах могут принимать любые значения («от - до»), то для этого признака нужно строить интервальный вариационный ряд.
Ранжированный вариационный ряд - это распределение отдельных единиц совокупности в порядке возрастания или убывания исследуемого признака.
Дискретный вариационный ряд характеризует распределение единиц совокупности по дискретному признаку, принимающему только целые значения.
Если признак имеет непрерывное изменение, которые в определенных границах могут принимать любые значения («от - до»), то для этого признака нужно строить интервальный вариационный ряд.
Слайд 4Задача. Имеется информация о количестве книг, полученных студентами по абонементу за
прошедший учебный год.
Слайд 5Построить ранжированный и дискретный вариационные ряды распределения, обозначив элементы ряда.
Слайд 7Построить ряд распределения, выделив 5 групп предприятий (с равными интервалами).
Решение
Для решения
выберем наибольшее и наименьшее значения стоимости основных фондов предприятий. Это 30,0 и 10,2 тыс. руб.
Найдем размер интервала: h = (30,0-10,2):5= 3,96 тыс. руб.
Тогда в первую группу будут входить предприятия, размер основных фондов которых составляет от 10,2 тыс. руб. до 10,2+3,96=14,16 тыс. руб. Таких предприятий будет 9. Во вторую группу войдут предприятия, размер основных фондов которых составит от 14,16 тыс. руб. до 14,16+3,96=18,12 тыс. руб. Таких предприятий будет 16. Аналогично найдем число предприятий, входящих в третью, четвертую и пятую группы.
Найдем размер интервала: h = (30,0-10,2):5= 3,96 тыс. руб.
Тогда в первую группу будут входить предприятия, размер основных фондов которых составляет от 10,2 тыс. руб. до 10,2+3,96=14,16 тыс. руб. Таких предприятий будет 9. Во вторую группу войдут предприятия, размер основных фондов которых составит от 14,16 тыс. руб. до 14,16+3,96=18,12 тыс. руб. Таких предприятий будет 16. Аналогично найдем число предприятий, входящих в третью, четвертую и пятую группы.
Слайд 9Показатели вариационного ряда
Средняя арифметическая - это обобщающий показатель, характеризующий размер изучаемого признака.
Средняя арифметическая обозначается как M, представляет собой самый распространенный вид средней. Средняя арифметическая рассчитывается как отношение суммы значений показателей всех единиц наблюдения к числу всех исследуемых. Методика расчета средней арифметической различается для простого и взвешенного вариационного ряда.
Формула для расчета взвешенной средней арифметической:
M = Σ(V * P)/ n, V-варианта, Р- частота, n- объем выборки
Формула для расчета взвешенной средней арифметической:
M = Σ(V * P)/ n, V-варианта, Р- частота, n- объем выборки
Слайд 10Мода – еще одна средняя величина вариационного ряда, соответствующая наиболее часто повторяющейся
варианте. Или, если выразиться по другому, это варианта, которой соответствует наибольшая частота. Обозначается как Мо.
Например, в вариационном ряду значений частоты сердечных сокращений:
80, 84, 84, 86, 86, 86, 90, 94;
значение моды составляет 86, так как данная варианта встречается 3 раза, следовательно ее частота - наибольшая.
Медиана – значение варианты, делящей вариационный ряд пополам: по обе стороны от нее находится равное число вариант. Медиана также, как и средняя арифметическая и мода, относится к средним величинам. Обозначается как Me
Например, в вариационном ряду значений частоты сердечных сокращений:
80, 84, 84, 86, 86, 86, 90, 94;
значение моды составляет 86, так как данная варианта встречается 3 раза, следовательно ее частота - наибольшая.
Медиана – значение варианты, делящей вариационный ряд пополам: по обе стороны от нее находится равное число вариант. Медиана также, как и средняя арифметическая и мода, относится к средним величинам. Обозначается как Me