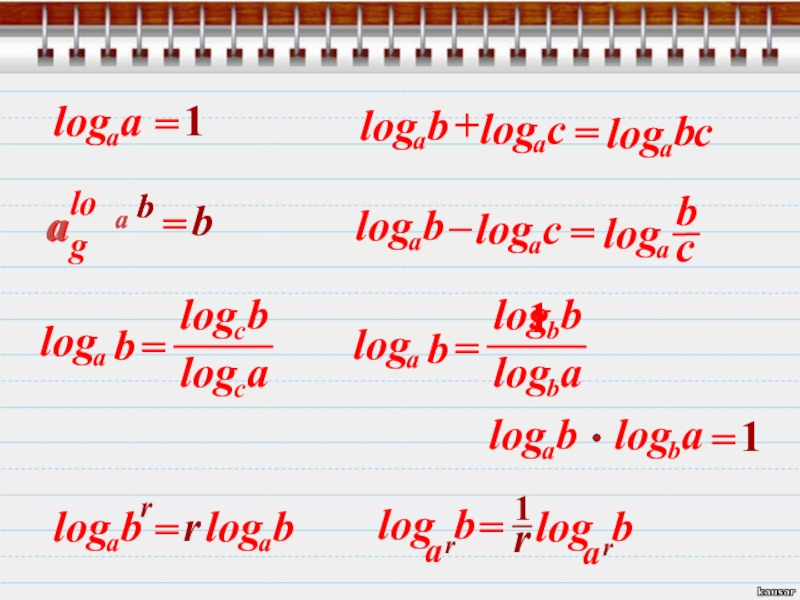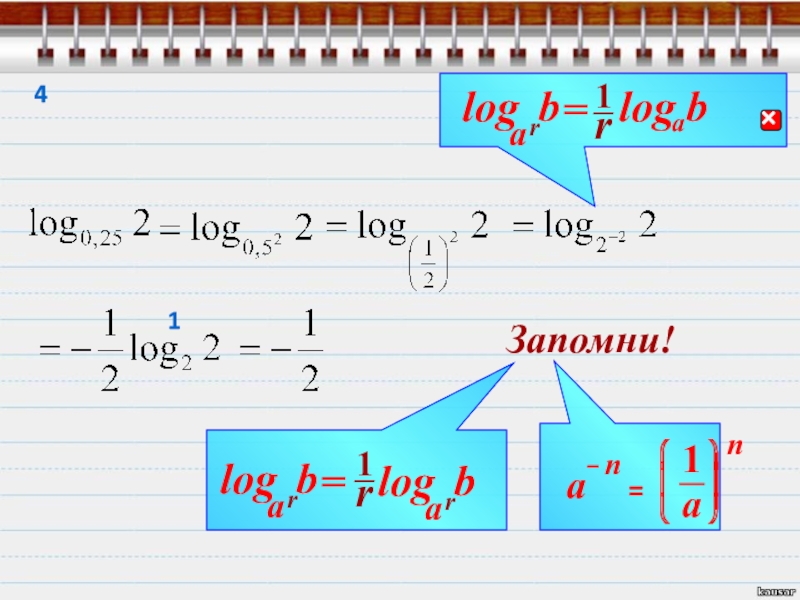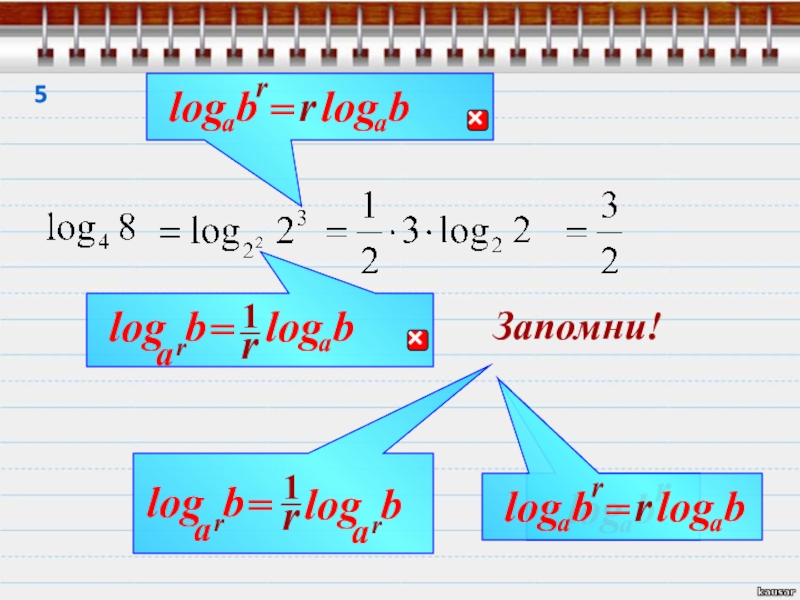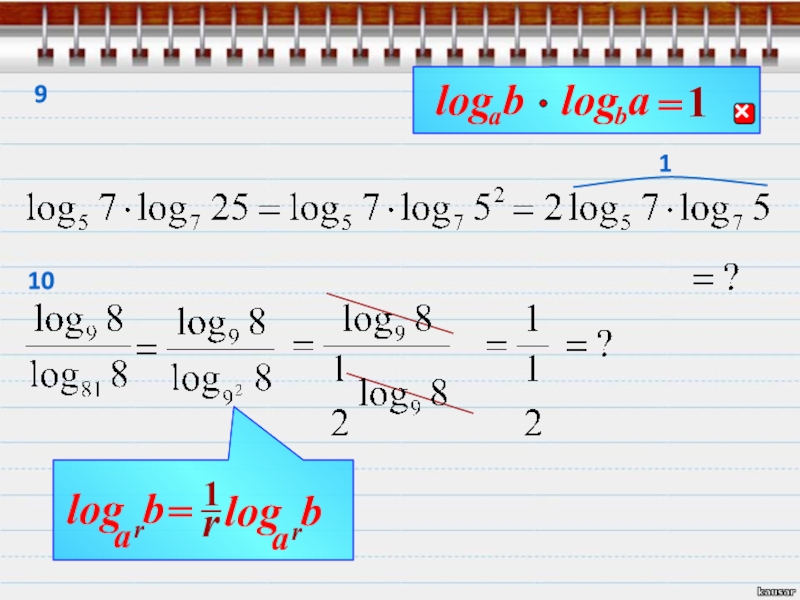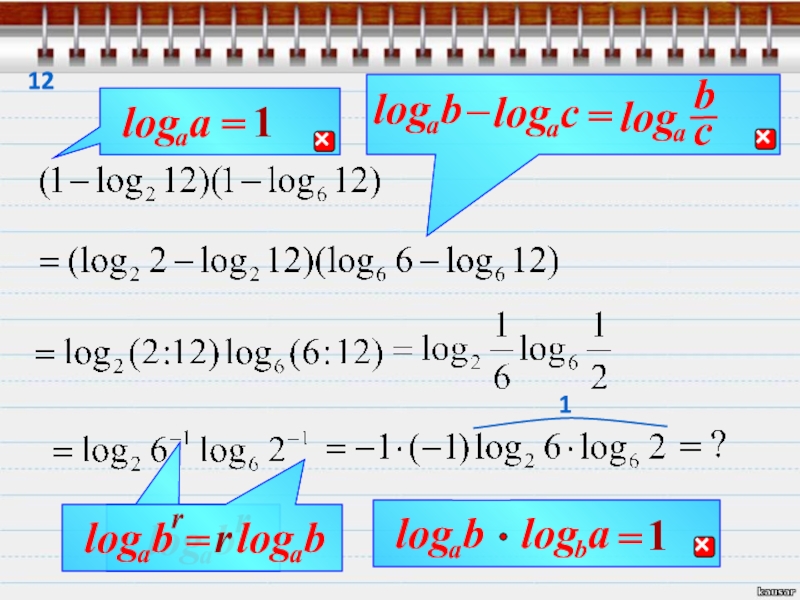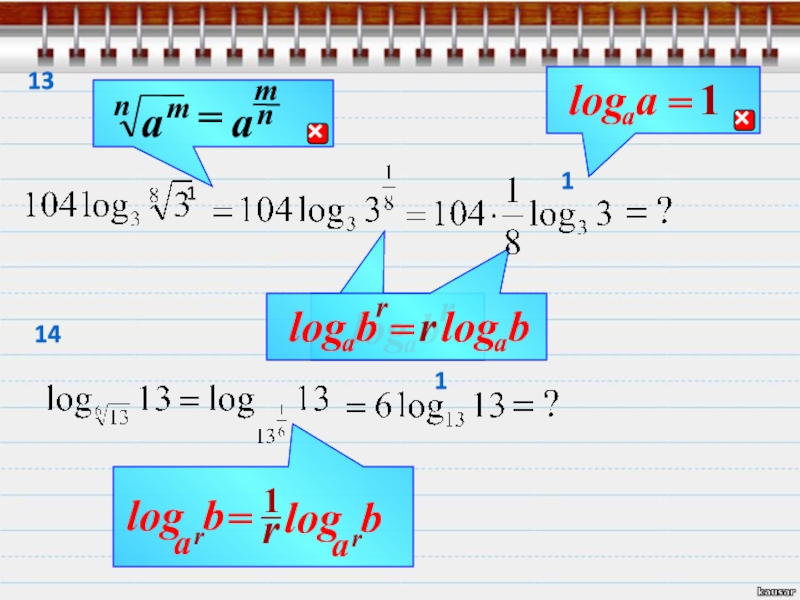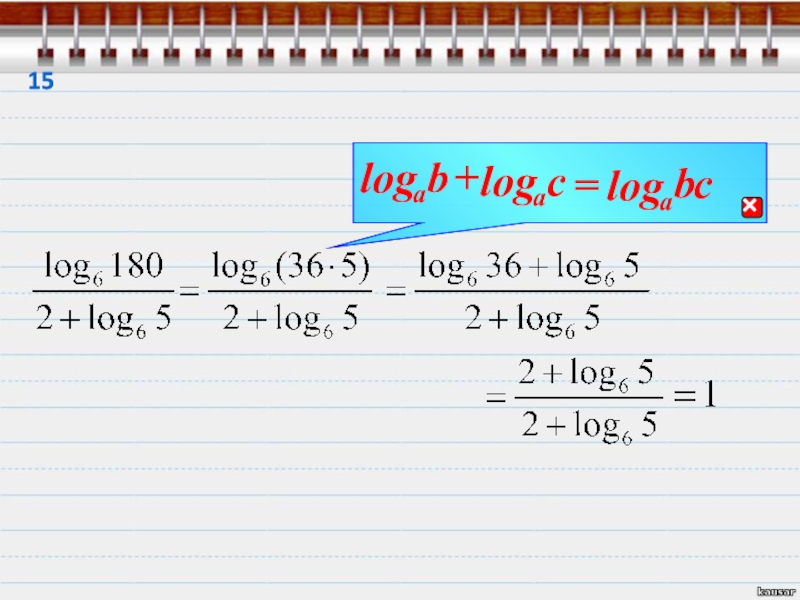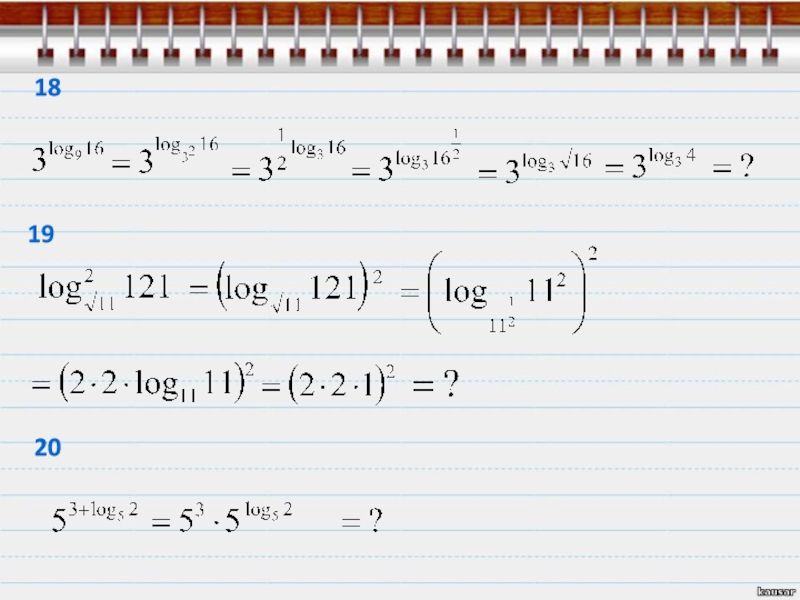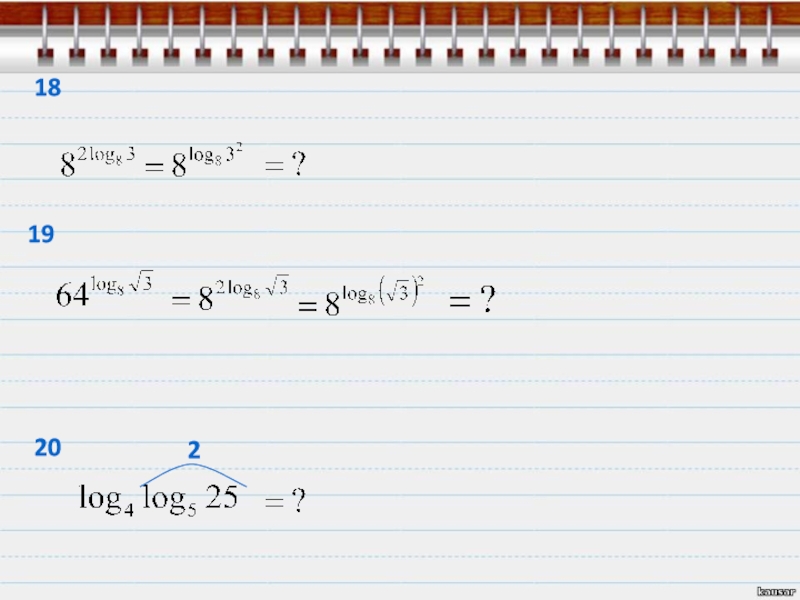- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике для студентов 1 курса ЛОГАРИФМЫ
Содержание
- 1. Презентация по математике для студентов 1 курса ЛОГАРИФМЫ
- 2. Что такое логарифм? Как решать логарифмы?
- 3. Для начала реши в уме вот такое
- 4. Закрепим результат и решим ещё одно показательное
- 5. А теперь реши почти то же самое:
- 6. 3x = 8 Можно, конечно, прикинуть,
- 7. вернёмся к примеру 3x = 8
- 8. Как решить пример5x = 12 ?Легко! х
- 9. Ещё пример 2x =135 ?Элементарно!х =
- 10. Ну так вот, на вопрос «чему равен
- 11. Слайд 11
- 12. Ну ладно, специально для тебя: инженерный калькулятор
- 13. Но
- 14. А log327 чему равен?
- 15. Поздравляю! Мы только что решали логарифмы!Вот мы
- 16. Запишем логарифм в общем виде, т.е. через
- 17. А если а = 0? Такая же
- 18. Что же получается?а > 0; a
- 19. Официальное определение логарифма числа выглядит так: ВНИМАНИЕ!!!Логарифмом
- 20. Тебе вовсе не помешает знать, что это
- 21. Нелишне будет познакомиться с такими логарифмами поближе:Десятичный
- 22. И контрольный «выстрел»:Да поможет тебе таблица умножения!В
- 23. Выражение «решение логарифмов» подразумевает не только их
- 24. logab = cМы уже знаем, что если
- 25. Это супер-свойство! Благодаря ему «многоэтажное» выражение, стоящее
- 26. Чему равняется выражение:logа1 = ?Ну в какую
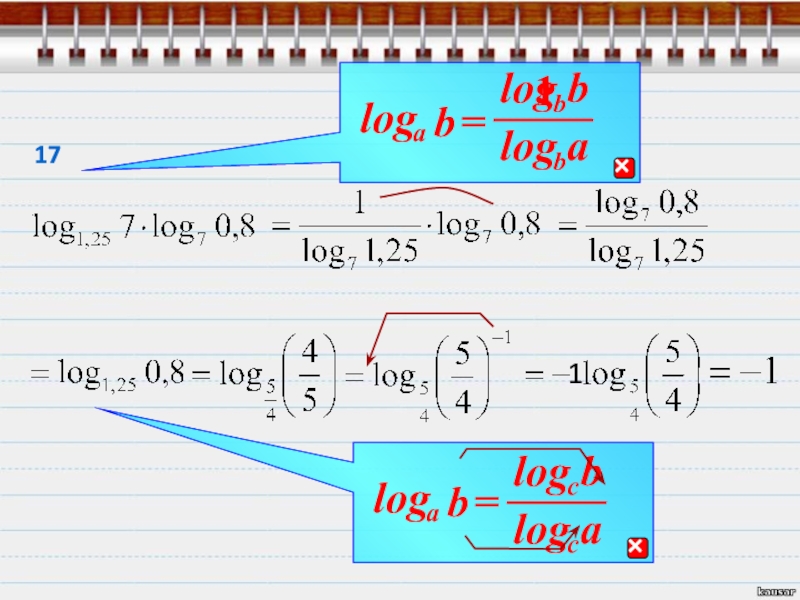
- 27. ==1==bralog
- 28. Вот и весь набор, решать-то как? Открываю
- 29. Найди значение выраженияВот как то так.Далее даны
- 30. r111
- 31. =r23
- 32. bralogЗапомни!=14
- 33. bralogЗапомни! r5
- 34. 67
- 35. 118
- 36. 1 bralog910
- 37. 111
- 38. 12 r1
- 39. 13 r11 bralog114
- 40. 15=
- 41. 161 r
- 42. 1711
- 43. 181920
- 44. 181920
- 45. Думаю, что теперь
- 46. http://www.egesdam.ru/page280.phpи материалы сайта При составлении пособия использованы презентация Савченко Е.М. « Свойства логарифмов. Готовимся к ЕГЭ»
- 47. СвойствалогарифмовГотовимся к ЕГЭ
Слайд 1 ЛОГАРИФМЫ
Пособие для студентов 1 курса
Составитель пособия С.А.Дроздова
Колледж строительства
2014 год
г.Астрахань
Слайд 2Что такое логарифм?
Как решать логарифмы?
Эти вопросы многих студентов
Слайд 3Для начала реши в уме вот такое уравнение:
3x = 9
Ну конечно же х=2
Всё просто: 32 = 9
!Три в квадрате - это девять!
Слайд 4Закрепим результат и решим ещё одно показательное уравнение
Получилось? Без сомнения!
Ответ: х=3, так как 33 = 27
!три в кубе равно двадцати семи!
Слайд 5А теперь реши почти то же самое:
3x = 8
Что, что-то не
Ответ, что «нету такого икса», не принимается! ОН ЕСТЬ!
Согласись, что это как-то нечестно – с девяткой пример решается в уме, также и с числом 27, а с восьмеркой не решается вовсе! Ну чем одни числа лучше других?! Да ничем! Никакой дискриминации! Для математики все числа равны! Ну, не буквально, конечно….
Слайд 63x = 8
Можно, конечно, прикинуть, что икс – какое-то
…или решить…графически
«Вот ещё!» - скажешь ты, не «царское это дело», да и так возиться каждый раз....
Ты прав, математика решает вопрос как всегда радикально и элегантно. Просто введением понятия логарифма. Итак, что такое логарифм?
Слайд 7 вернёмся к примеру
3x = 8
х -
Прочитай фразу ещё и ещё раз. Это важно.
Вот это число и называется логарифмом восьми по основанию три.
Записывается это вот как: х = log38
Читаем это: "икс равен логарифму восьми по основанию три".
Где что пишется – запомнить легко: число 3 – называется основанием, пишется в логарифме и в показательном выражении внизу.
Это и есть ответ!
Мы решили загадочное показательное уравнение 3x = 8!
Ответ: х = log38 .
И ничего не надо «прикидывать» и считать!
Слайд 8Как решить пример
5x = 12 ?
Легко! х - это число, в
В математической записи:
х = log512
Пример решён!
Слайд 9Ещё пример 2x =135 ?
Элементарно!
х = log2135
А ещё один
Не вопрос!
х = log190,352
Здорово, правда? И ничего считать не надо.
Слайд 10Ну так вот, на вопрос
«чему равен х в уравнении 3x
мы теперь смело отвечаем: «х равен числу, в которое надо возвести 3, чтобы получить 8!».
Или, чтобы так долго не говорить, пишем в сокращённом варианте, через логарифм:
х = log38
и точка!
Слайд 11 Догадываюсь, что тебя
Пусть тебя не смущают эти значки: логарифмы –это обыкновенные числа, которые записываются не привычными цифрами, а странным, зашифрованным способом.
Слайд 12Ну ладно, специально для тебя: инженерный калькулятор показывает это конкретное число:
Легче стало? Учти ещё, что это число бесконечно. Иррациональное оно... И записать его можно только приблизительно. Вот так-то!
Запись числа с помощью логарифма удобнее, короче, а главное – точное! Не то, что бесконечные страшные лохматые числа. А кому надо числовой ответ - посчитает на калькуляторе. Нам то с тобой – не надо…
Как же расшифровать это число
log38
и записать в привычном виде цифрами?
Слайд 13 Но есть логарифмы, которые считаются
Переведём с математического на русский: log24 - это число, в которое надо возвести 2 (основание), чтобы получить 4.
Ну, во что надо возвести 2, чтобы получить 4!?
Да! В квадрат(двойку) надо возвести!
Вот и ответ: log24 = 2
Слайд 14А log327 чему равен?
В какую степень
Правильно, в третью!
Ответ: log327 = 3
Дошло? Закрепим успех! Решаем примеры:
log381 =
log416 =
log55 =
log6216 =
Ответы (в беспорядке, разумеется!): 2; 1; 3; 4.
Что, тяжело сообразить, в какую степень надо возвести шестёрку, чтоб 216 получить? Ну, друг, таблицу умножения знать надо! Надо… и не только здесь.
Слайд 15Поздравляю! Мы только что решали логарифмы!
Вот мы и познакомились с логарифмами
есть кое-какие детали и мы о них узнаем прямо сейчас
Слайд 16Запишем логарифм в общем виде, т.е. через буквы:
c = logab
или,
Вспомним: а - это основание, которое нужно возвести в степень с, чтобы получить b.
Прикинем, любым ли числом может быть а?
Если, к примеру, а = 1?
В какую же степень надо возвести единицу, чтобы получить… b?
Верно! В любую! Как ни крути и b тоже будет единицей! 1с =1
!единица в любой степени – единица!
Как-то оно не очень...И даже не интересно… Как не меняй с,а а и b единичками останутся...
Тогда так: вводим ограничение a ≠ 1 !!!
Слайд 17А если а = 0?
Такая же история!
0с =0
Не
А отрицательные числа и вовсе - капризные. В одну степень их можно возводить, в другую нельзя... Вот и поступили с ними, как со всеми капризными – вовсе исключили из рассмотрения.
logab = c
Слайд 18Что же получается?
а > 0; a ≠ 1
А вот если
b > 0.
Вот такие ограничения. Только на а и b! А вот с может получиться абсолютно любым числом. При решении числовых логарифмов эти ограничения практически не сказываются. Они понадобятся при решении логарифмических уравнений и неравенств.
logab = c
Слайд 19Официальное определение логарифма числа выглядит так: ВНИМАНИЕ!!!
Логарифмом числа b>0 по основанию
Напомню, так, на всякий случай: логарифм числа b по основанию a обозначается logab
Определение логарифма
Слайд 20Тебе вовсе не помешает знать, что это такое.
В математике два основания
Число е.
е = 2,71828182845.....Иррациональное число. Сплошь и рядом попадается в высшей математике. Само попадается, его не придумали. Почему попадается – да кто его знает...
Логарифмы по этим основаниям пишут покороче:
log10b = lgb
!Основание 10 не пишется и буква "о" пропадает!
Такие логарифмы называются десятичными.
logeb = lnb
Логарифмы по основанию "е" называются натуральными. Что уж тут натурального…
Эти логарифмы ничем не отличаются от всех остальных! Ни по определению, ни по свойствам! Решение этих логарифмов ничем не отличается от решения обычных!
Десятичные и натуральные логарифмы
Слайд 21Нелишне будет познакомиться с такими логарифмами поближе:
Десятичный логарифм единицы равен… равен…
В
Я думаю, пара-тройка примеров закрепит наш успех:
Почему? Да пожалуйста!
Ну? В какую степень надо возвести десятку, чтобы получить 1000?
Ну конечно же в третью!!!
Слайд 22И контрольный «выстрел»:
Да поможет тебе таблица умножения!
В какую степень надо возвести
Что-то тебе подсказывает ( скорее всего, таблица умножения), что чтобы получить 100, то десятку надо возвести во вторую степень
А чтобы получить одну сотую, то… то… Ну конечно же в минус вторую!!!
Аналогично:
Ну вот. Теперь ты всё знаешь. Пора переходить к более серьёзным логарифмам.
Слайд 23Выражение «решение логарифмов» подразумевает не только их вычисления, но и преобразования.
Свойства логарифмов
Слайд 24logab = c
Мы уже знаем, что если число а (основание) возвести
ac = b
А теперь смотрим, чему же равно число с? Да вот оно:
с = logаb
Подставим это в предыдущую формулу, и получим:
Слайд 25Это супер-свойство!
Благодаря ему «многоэтажное» выражение, стоящее слева от знака
Это свойство называют ещё определением логарифма
Оно же «основное логарифмическое тождество»
Всё просто!
Слайд 26Чему равняется выражение:
logа1 = ?
Ну в какую степень надо возвести а,
Таблица умножения подкачала? Нет?
!Любое число в нулевой степени равно 1! Да, в нулевую! Вот и пишем:
logа1 = 0
Следующее свойство уже не требует разъяснений:
logаа = 1
Оставшиеся свойства логарифмов выводить не будем, я их приведу сразу в комплекте. Этот комплект надо знать! Это основа для решения логарифмов.
Ну так, на всякий случай:
а1 =а
Слайд 28Вот и весь набор, решать-то как? Открываю тайну. Все задания на
log142 + log147 = ?
По отдельности оба логарифма ровно не считаются. Смотрим на формулы - свойства и выбираем подходящую. Это первая во втором столбце формула.
log142 + log147 = log14(2·7) = log1414 = 1
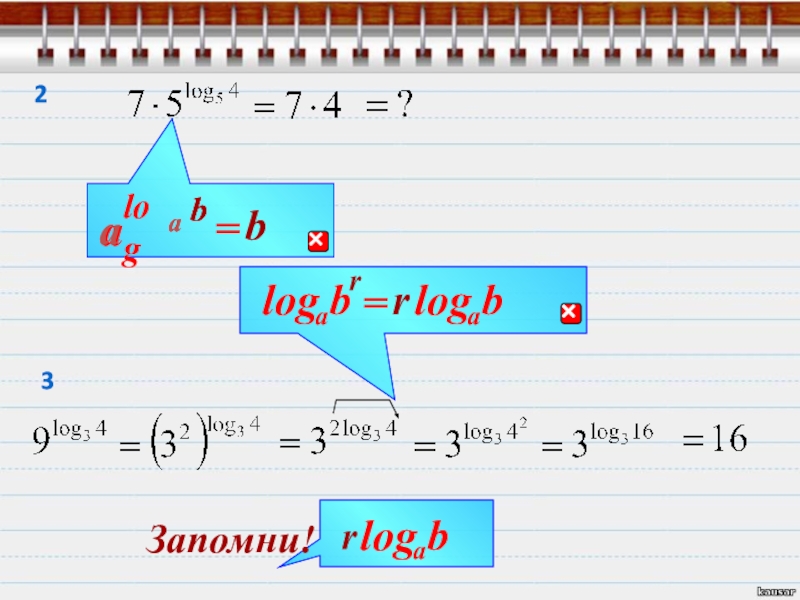
Слайд 29Найди значение выражения
Вот как то так.
Далее даны практические советы по решению
Во всех примерах только одна цель
Дерзай!
Слайд 45Думаю, что теперь
Не за горами экзамен по математике…
У тебя ВСЁ получится!
ТЕРПЕНЬЕ И ТРУД ВСЁ ПЕРЕТРУТ :-)