- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике для старших классов Применение производной и первообразной показательной и логарифмической функции
Содержание
- 1. Презентация по математике для старших классов Применение производной и первообразной показательной и логарифмической функции
- 2. Цели урока: Обобщение изученного материала по
- 3. «Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным»ПаскальДевиз урока
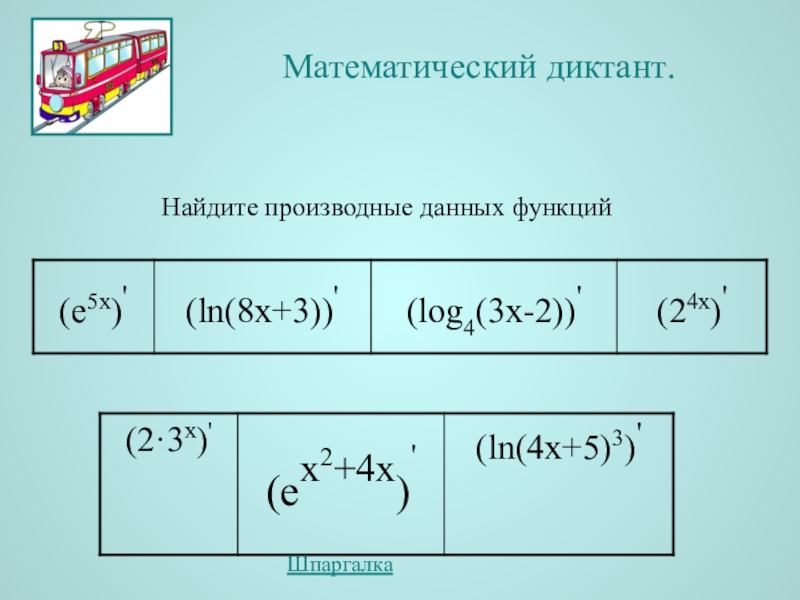
- 4. Найдите производные данных функцийМатематический диктант.Шпаргалка
- 5. Выберите букву соответствующую вашему ответу.
- 6. Решение задач.Внимание! Перед нами здание городской мэрии.
- 7. Слайд 7
- 8. А теперь мы попали на завод.Из цилиндрического
- 9. Решение.Так как радиус большего основания равен 8
- 10. Алгоритм решения задач.Строим график функций.Находим пределы интегрирования.С помощью вычисляем площадь фигуры или объем тела.
- 11. Самостоятельная работа.Задание:Вычислите площадь фигуры, ограниченной линиями:Вариант 1А:
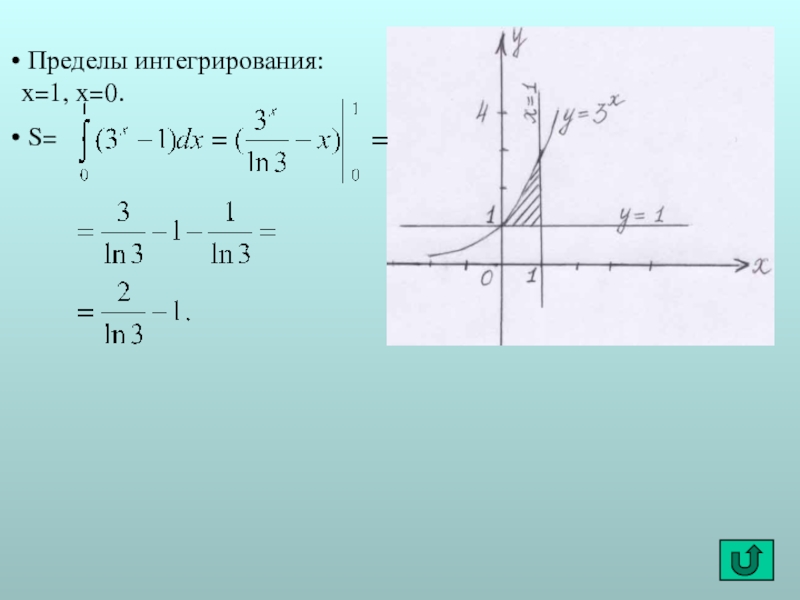
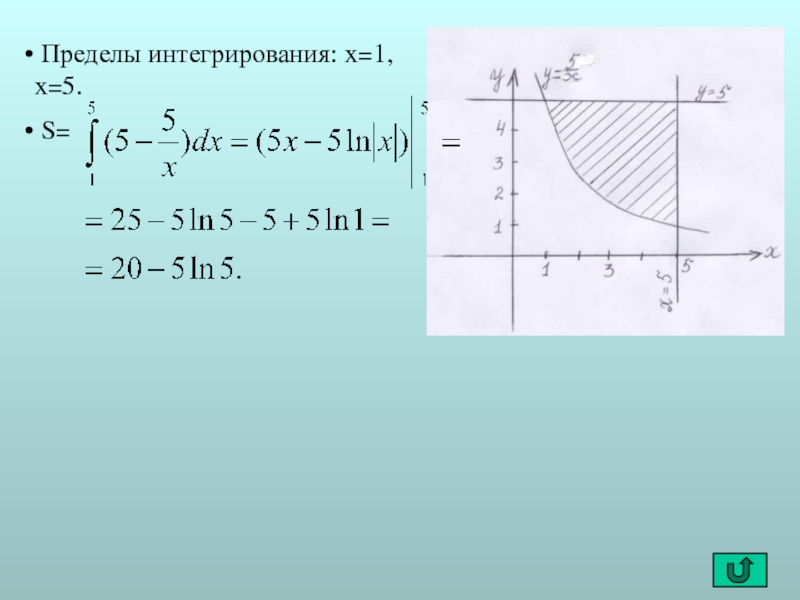
- 12. Пределы интегрирования: x=1, x=0. S=
- 13. Пределы интегрирования: x=1, x=5. S=
- 14. Рефлексия.А. У меня по этой теме прочные
- 15. Придумать задачу на вычисление площади или объема фигуры с практическим содержанием.
- 16. Шпаргалка(ax)’ = ax lna (ex)’= ex(lnx)’=1/x(logax)’=1/(x lna)Для возвращения нажмите на стрелку.Ln4 ≈ 1,4
Слайд 2Цели урока:
Обобщение изученного материала по теме.
Формирование умений
Развитие познавательной активности, творческих способностей.
Воспитание интереса к предмету.
Слайд 3«Предмет математики настолько серьезен, что полезно не упускать случая делать его
Паскаль
Девиз урока
Слайд 6Решение задач.
Внимание! Перед нами здание городской мэрии.
x=4; y=6
Кроме того, выполнив
Сколько денег он получит от мэрии?
Перед зданием решено разбить клумбу. Но по форме клумба не должна быть круглой, квадратной и прямоугольной. Она должна содержать в себе прямые и кривые линии.
Учитывая эти условия, один ученый предложил придать клумбе форму плоской фигуры, которую можно было бы ограничить линиями:
Слайд 7
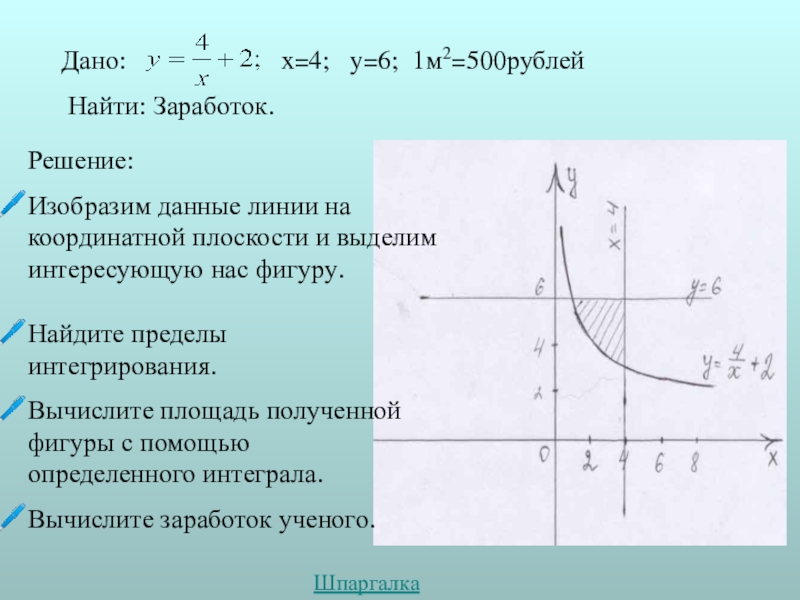
Найти: Заработок.
Решение:
Изобразим данные линии на координатной плоскости и выделим интересующую нас фигуру.
Найдите пределы интегрирования.
Вычислите площадь полученной фигуры с помощью определенного интеграла.
Вычислите заработок ученого.
Дано:
Шпаргалка
Слайд 8А теперь мы попали на завод.
Из цилиндрического бруса радиусом 8дм и
Каков объем подставки?
Шпаргалка
Слайд 9
Решение.
Так как радиус большего основания равен 8 дм, то проведем линию
2х =8 ,2х =23, х=3.
Так как высота подставки 2дм, то другой предел интегрирования х= 3 -2=1
Вычислим объем тела вращения с помощью определенного интеграла:
1
3
На координатной плоскости изобразим линию у=2х.
Определим форму подставки. Так как основаниями служат круги, то это – тело вращения.
Изобразим тело вращения.
Слайд 10Алгоритм решения задач.
Строим график функций.
Находим пределы интегрирования.
С помощью вычисляем
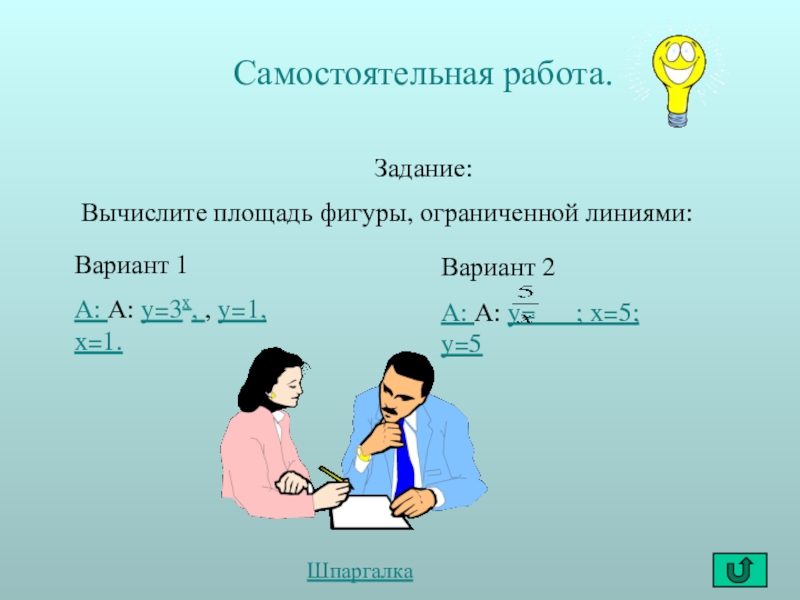
Слайд 11Самостоятельная работа.
Задание:
Вычислите площадь фигуры, ограниченной линиями:
Вариант 1
А: А: y=3x, , y=1,
Вариант 2
А: А: y= ; x=5; y=5
Шпаргалка
Слайд 14Рефлексия.
А. У меня по этой теме прочные знания.
Б. Я усвоил материал
В. Я мало понял. Мне необходимо работать.