- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии по теме Теорема, обратная данной
Содержание
- 1. Презентация по геометрии по теме Теорема, обратная данной
- 2. Теорема – этоутверждение, справедливость которого устанавливается путем рассуждений, т.е. доказательством.
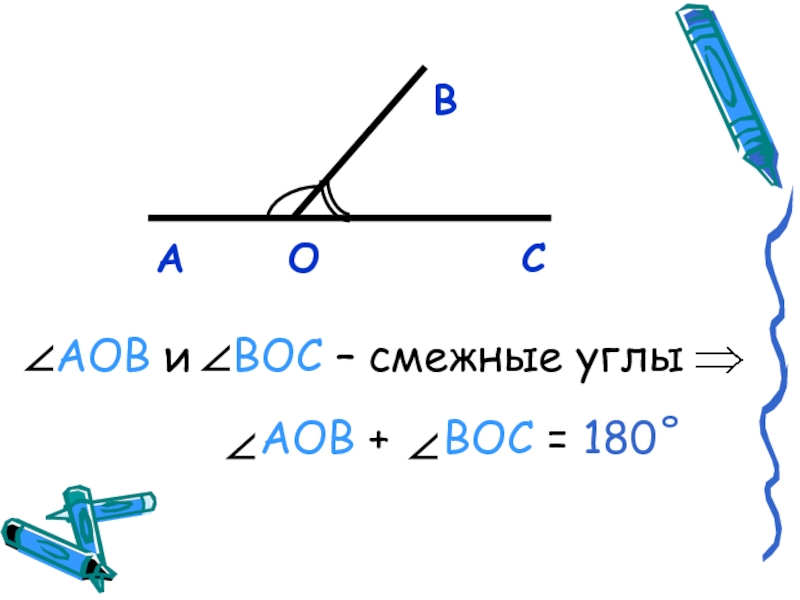
- 3. ВАОСАОВ и ВОС – смежные углы
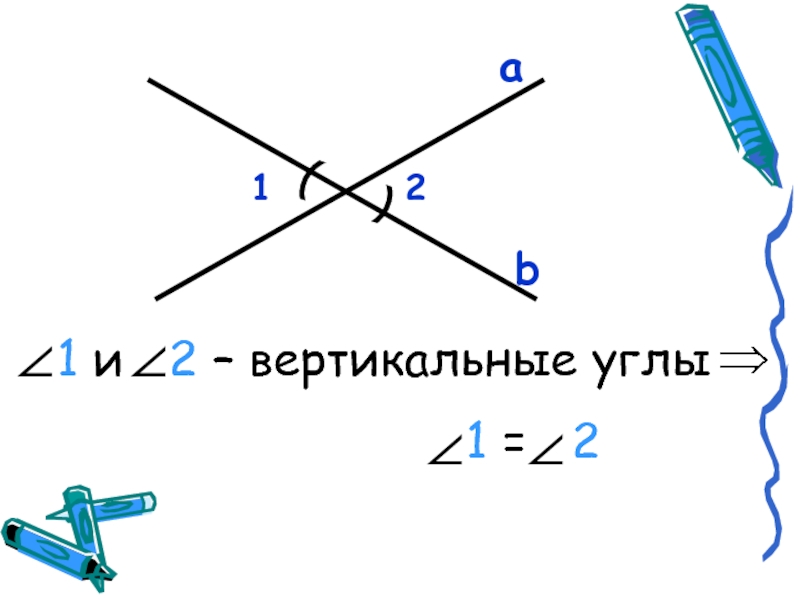
- 4. 12аb 1 и 2 – вертикальные
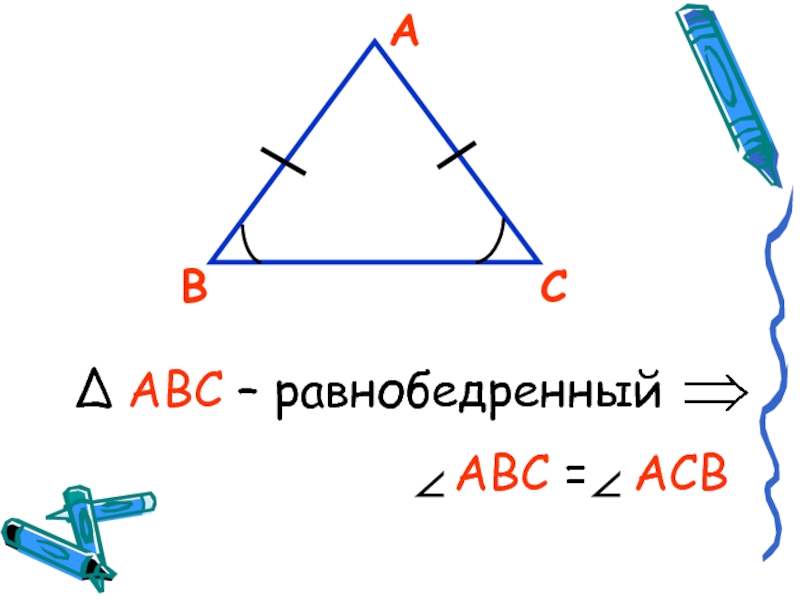
- 5. АВС∆ АВС – равнобедренный
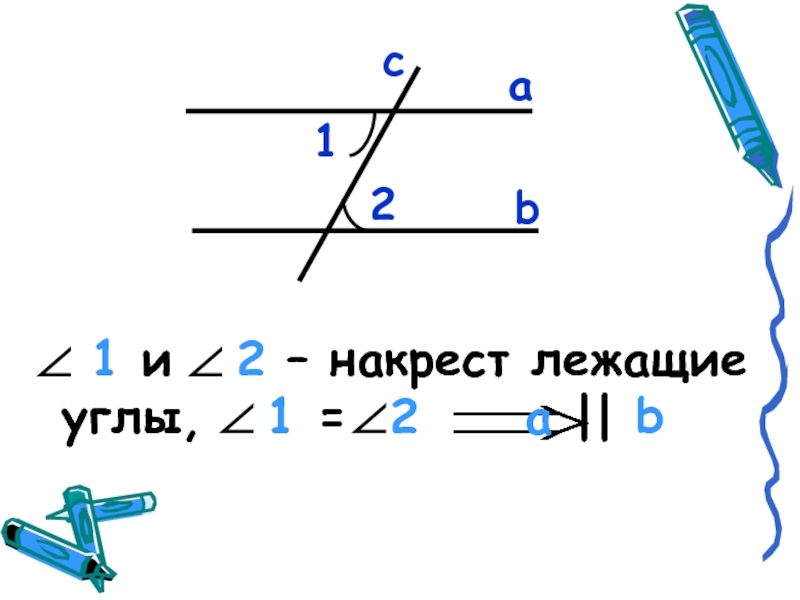
- 6. аb12c 1 и 2 – накрест
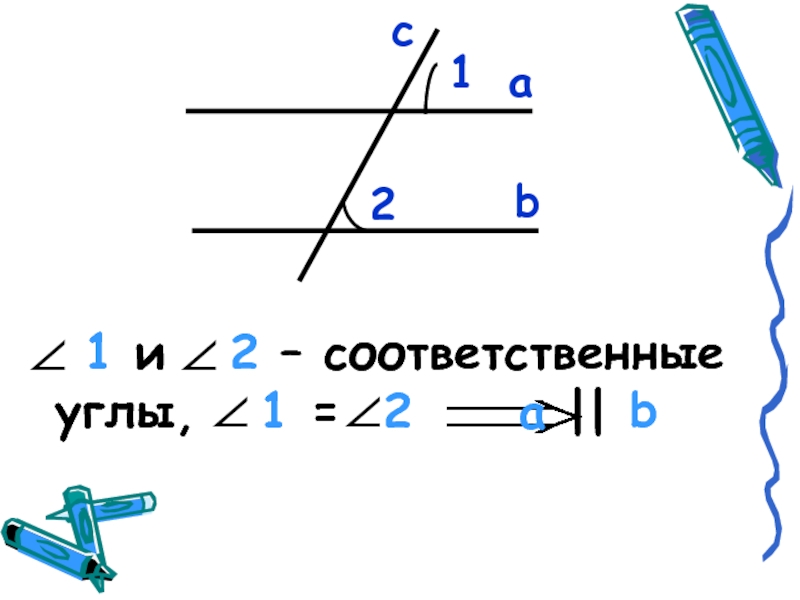
- 7. аb12c 1 и 2 – соответственные
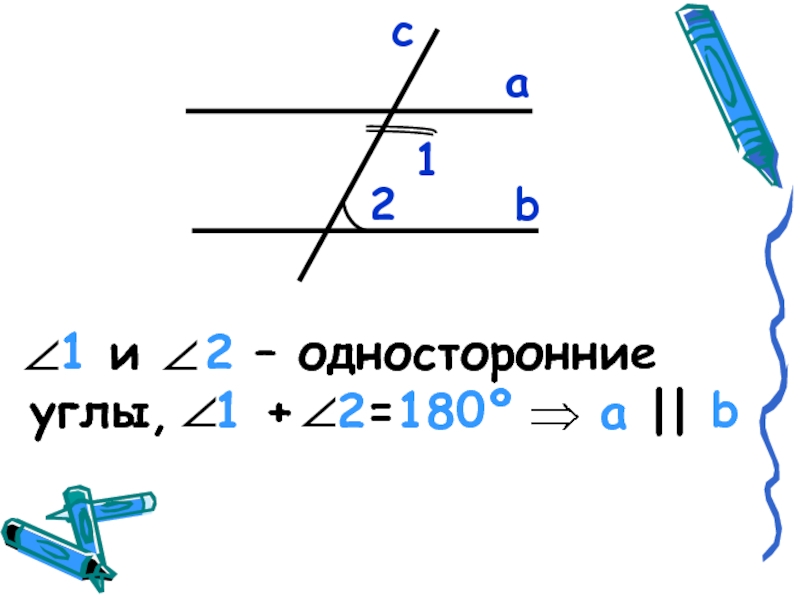
- 8. аb12c 1 и 2 – односторонние углы, 1 + 2=180º а || b
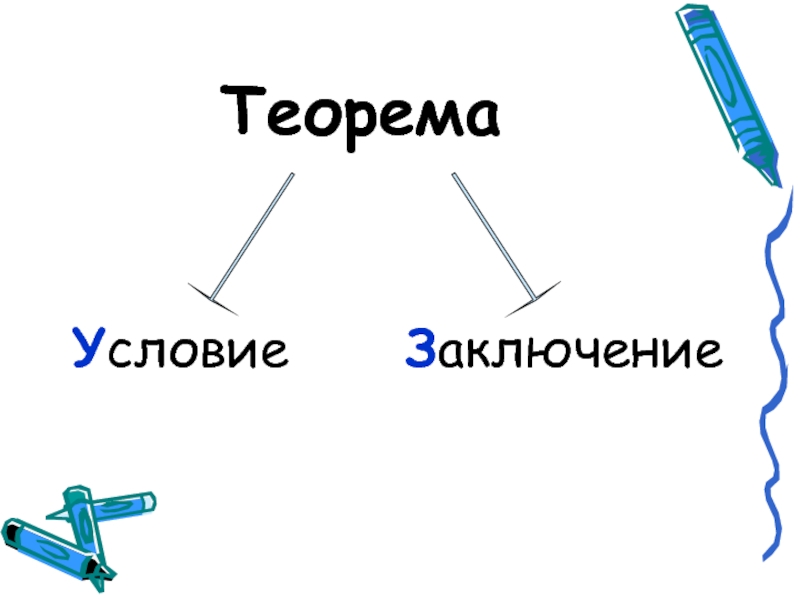
- 9. Теорема Условие Заключение
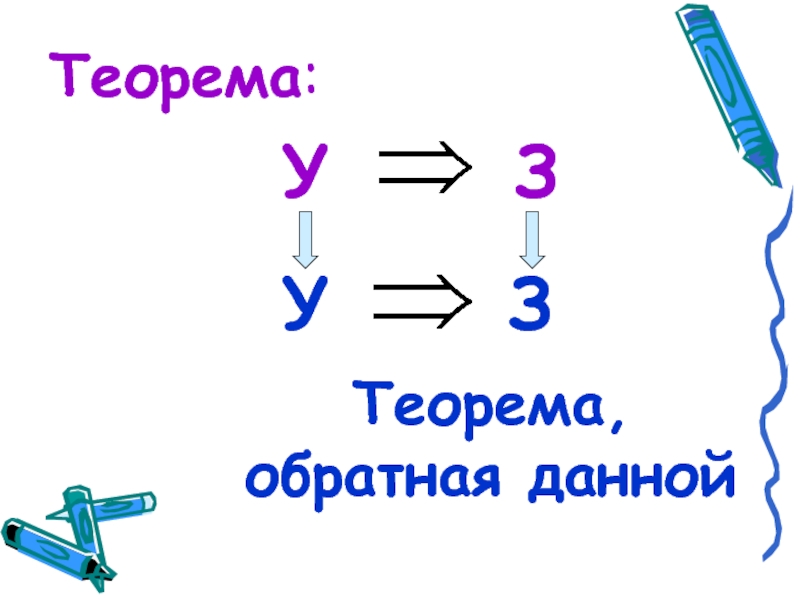
- 10. УЗТеорема:УЗТеорема, обратная данной
- 11. Теоремой, обратной данной называется такая теорема, в
- 12. Теорема:Если два угла смежные, то их сумма
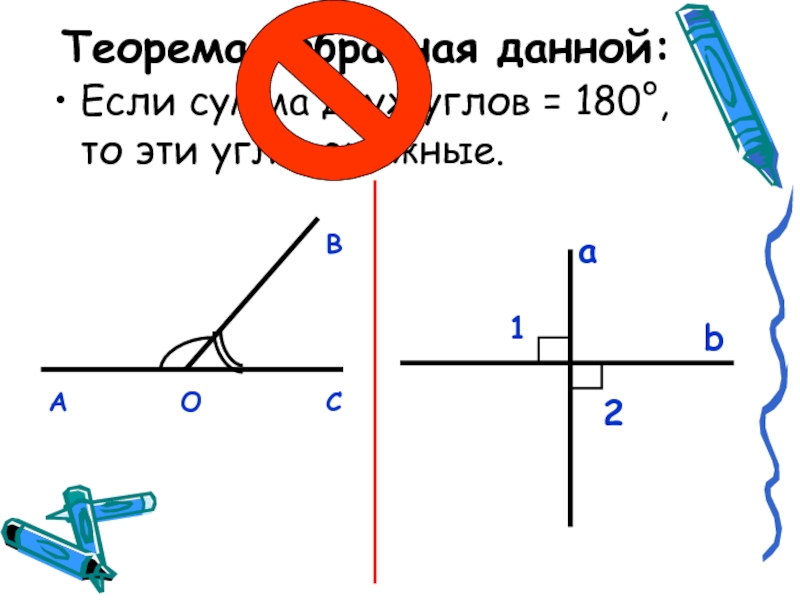
- 13. Теорема, обратная данной:Если сумма двух углов = 180°, то эти углы смежные.ВАОСаb12
- 14. Теорема:Если треугольник равнобедренный, то углы при основании
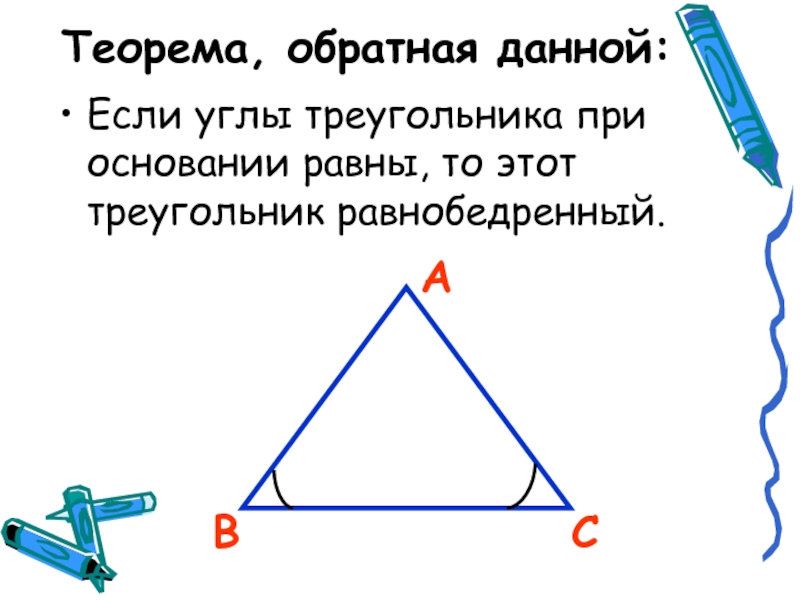
- 15. АВСТеорема, обратная данной:Если углы треугольника при основании равны, то этот треугольник равнобедренный.
- 16. Если при пересечении двух прямых секущей
- 17. Если при пересечении двух прямых секущей соответственные
- 18. Если при пересечении двух прямых секущей сумма
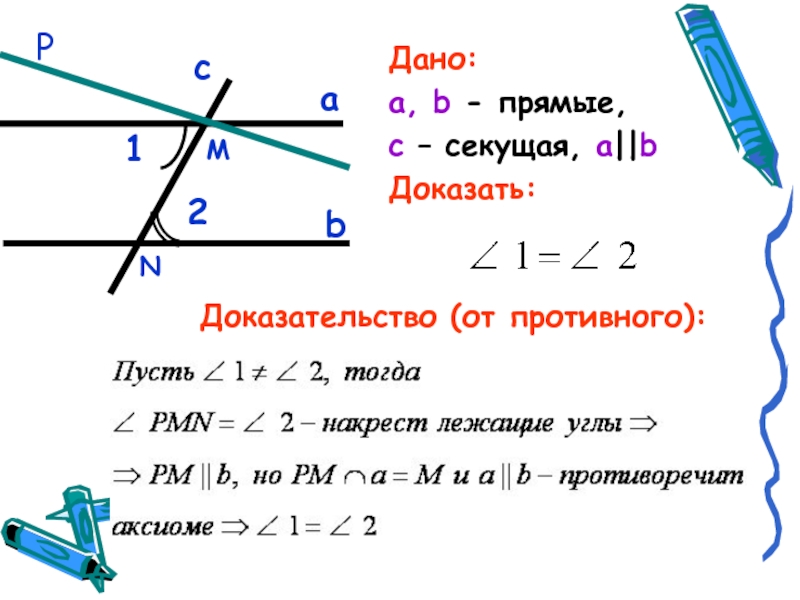
- 19. Дано:а, b - прямые, c – секущая, а||b Доказать: аb12cМРДоказательство (от противного):N
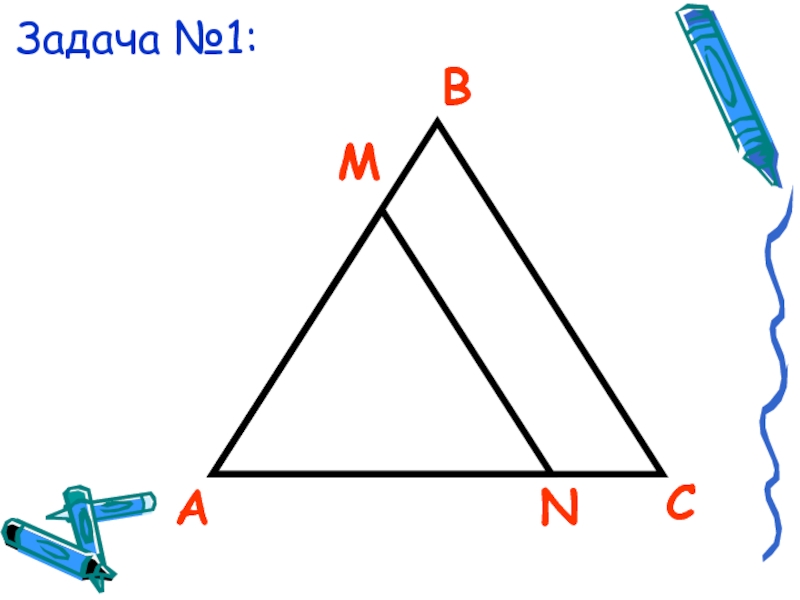
- 20. Задача №1:АСВМN
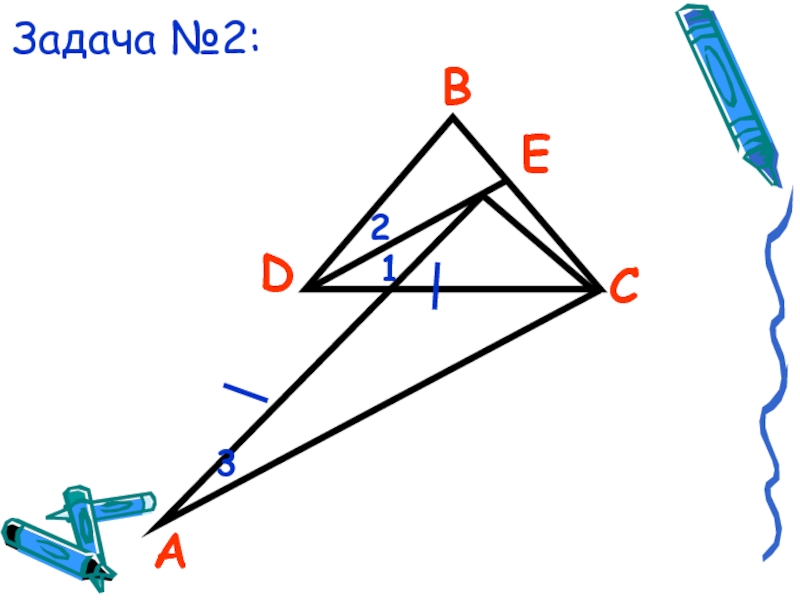
- 21. Задача №2:АВDEС312
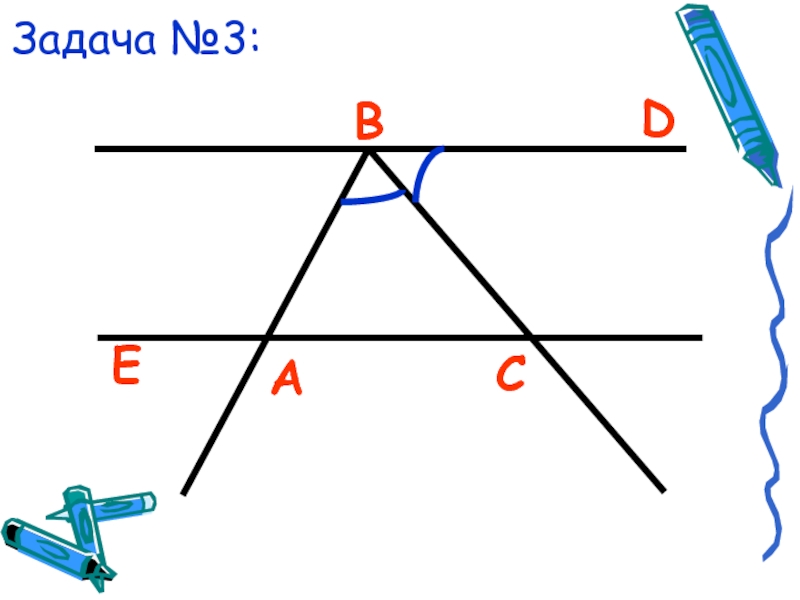
- 22. Задача №3:АВDEС
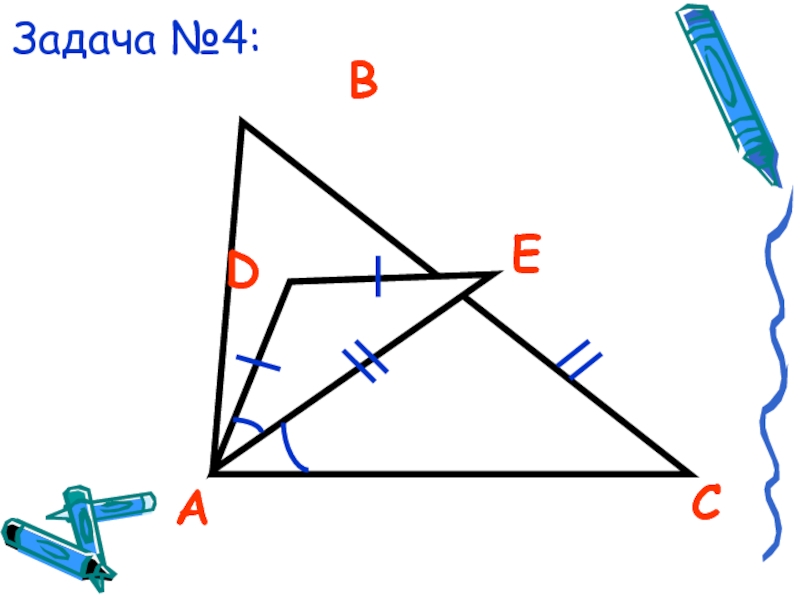
- 23. Задача №4:АСВDE
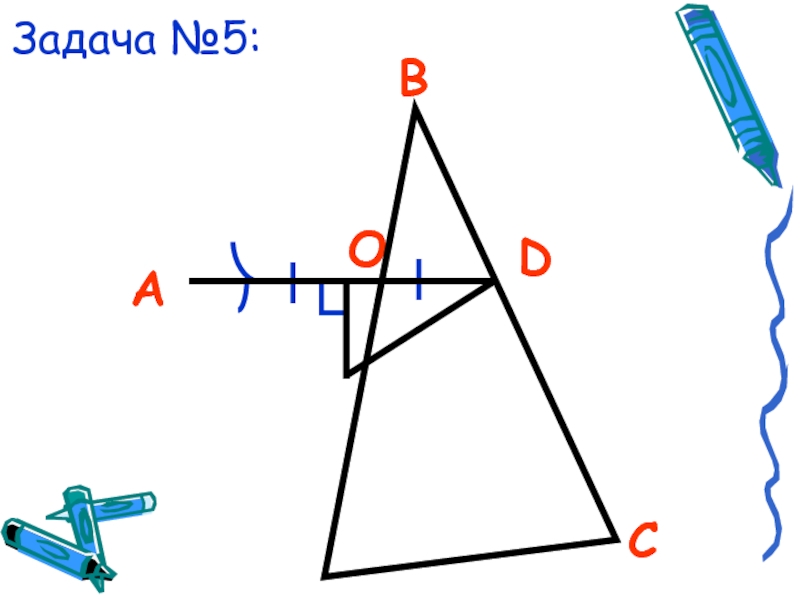
- 24. Задача №5:АСВDO
- 25. Урок закончен
Теорема – этоутверждение, справедливость которого устанавливается путем рассуждений, т.е. доказательством.
Слайд 2Теорема – это
утверждение, справедливость которого устанавливается путем рассуждений, т.е. доказательством.
Слайд 11Теоремой, обратной данной называется такая теорема, в которой условием является заключение
данной теоремы, а заключением – условие данной теоремы.
Слайд 12Теорема:
Если два угла смежные, то их сумма = 180°.
Теорема, обратная
данной:
Если сумма двух углов = 180°, то эти углы смежные.
Слайд 14Теорема:
Если треугольник равнобедренный, то углы при основании равны.
Теорема, обратная данной:
Если углы
треугольника при основании равны, то этот треугольник равнобедренный.
Слайд 15
А
В
С
Теорема, обратная данной:
Если углы треугольника при основании равны, то этот треугольник
равнобедренный.
Слайд 16 Если при пересечении двух прямых секущей накрест лежащие углы равны,
то прямые параллельны.
Теорема, обратная данной:
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Теорема, обратная данной:
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Слайд 17Если при пересечении двух прямых секущей соответственные углы равны, то прямые
параллельны.
Теорема, обратная данной:
Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Теорема, обратная данной:
Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Слайд 18Если при пересечении двух прямых секущей сумма односторонних углов = 180°,
то прямые параллельны.
Теорема, обратная данной:
Если две прямые пересечены секущей, то сумма односторонних углов равна 180°.
Теорема, обратная данной:
Если две прямые пересечены секущей, то сумма односторонних углов равна 180°.