- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по дискретной математике Элементы теории графов
Содержание
- 1. Презентация по дискретной математике Элементы теории графов
- 2. ВВЕДЕНИЕ Теория графов – часть дискретной математики,
- 3. Однажды великому математику Леонарду Эйлеру был задан
- 4. На карте старого Кёнигсберга был ещё один
- 5. Применение Анализ и проектирование сетей электроснабжения, водоснабжения,
- 6. Опр. Граф это множество вершин V={v1,v2,…vn} и
- 7. Опр. Граф это множество вершин V={v1,v2,…vn} и
- 8. Смешанный графСмешанный графНеориентированный графОриентированный графребродугавершинаМультиграфПсевдографКратные ребра и дугипетля
- 9. Смежные вершиныСмежные ребра (дуги)v1v2v3v4e1e6e5e4e3e2Ребро e5 инцидентное вершинам
- 10. Опр. Степенью vi вершины графа G, обозначаемой
- 11. Сумма полустепеней исходов (заходов) в орграфе G
- 12. Опр. Граф G называется полным, если он
- 13. Граф G={V,E} называется двудольным, если множество его
- 14. Паросочетанием графа G={V,E} называется подмножество его ребер
- 15. Граф G={V,E} называется взвешенным, если его ребрам (дугам) приписаны веса.Взвешенный граф часто называют сетьюabcde4562,32,583
- 16. abgjfedc261,51,21,16,52,52,50,82,03,10,85,521,2a исток сети (начальная вершина графа)J сток
- 17. Маршрутом в неориентированном графе G={V,E} называется такая
- 18. Маршрут называется цепью, если каждое ребро графа
- 19. Гамильтоновым циклом в графе G={V,E} называется цикл,
- 20. Вершины ei, ek графа G={V,E} называются связанными,
- 21. Связный ациклический граф называется деревом. Вершина дерева,
- 22. Дерево, у которого одна вершина выделяется среди
Слайд 2ВВЕДЕНИЕ
Теория графов – часть дискретной математики, геометрический подход к изучению
Истоки: задача о Кенигсбергских мостах, о расстановке ферзей, о перевозке грузов и др.
Слайд 3Однажды великому математику Леонарду Эйлеру был задан вопрос: можно ли обойти
Слайд 4На карте старого Кёнигсберга был ещё один мост, появившийся чуть позже,
Слайд 5Применение
Анализ и проектирование сетей электроснабжения, водоснабжения, газоснабжения, телефонизации.
Анализ и
Проектирование и возведение строительных объектов.
Разработка новых технологий и изделий
Разработка и эксплуатация компьютерных сетей. Маршрутизация данных в Интернете и т.д.
Слайд 6Опр. Граф это множество вершин V={v1,v2,…vn} и множество неупорядоченных и упорядоченных
Неупорядоченная пара вершин называется ребром, а упорядоченная дугой.
Граф содержащий только ребра называется неориентированным.
Граф содержащий только дуги называется ориентированным или орграфом.
Слайд 7Опр. Граф это множество вершин V={v1,v2,…vn} и множество неупорядоченных и упорядоченных
Неупорядоченная пара вершин называется ребром, а упорядоченная дугой.
Граф содержащий только ребра называется неориентированным.
Граф содержащий только дуги называется ориентированным или орграфом.
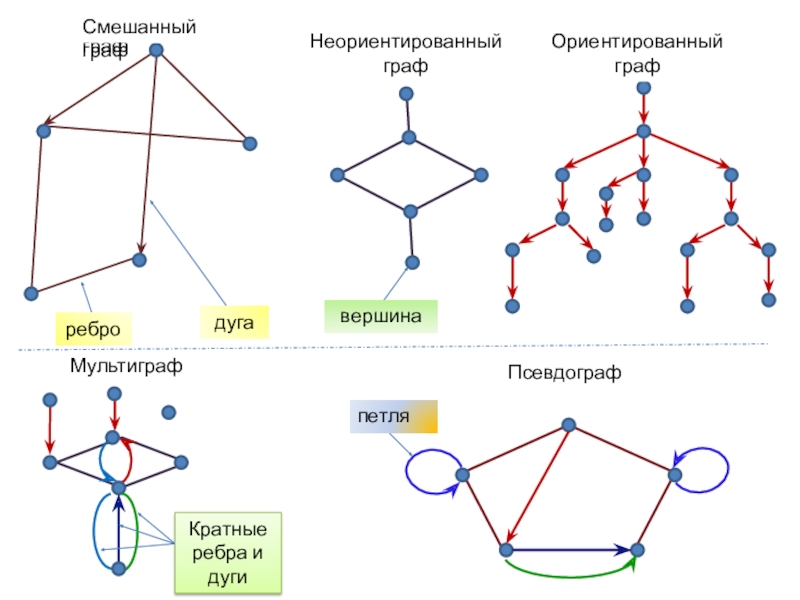
Слайд 8Смешанный граф
Смешанный граф
Неориентированный граф
Ориентированный граф
ребро
дуга
вершина
Мультиграф
Псевдограф
Кратные ребра и дуги
петля
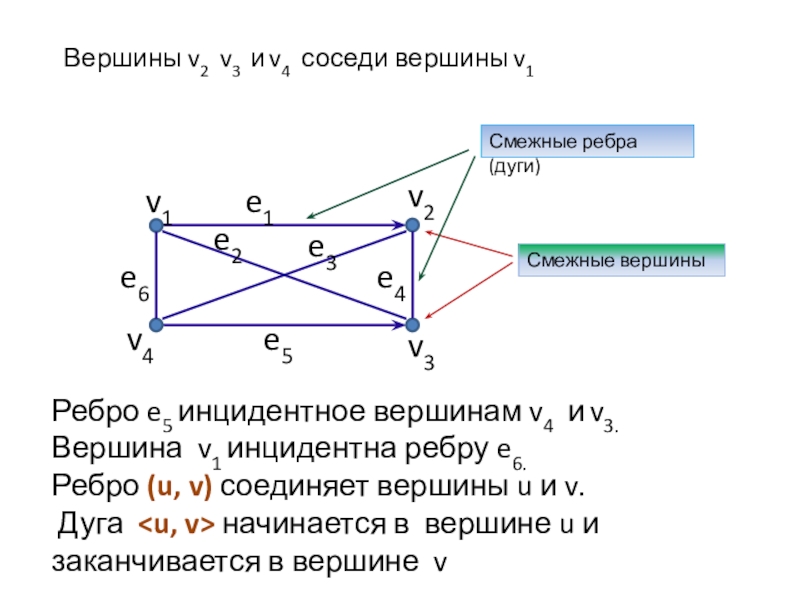
Слайд 9Смежные вершины
Смежные ребра (дуги)
v1
v2
v3
v4
e1
e6
e5
e4
e3
e2
Ребро e5 инцидентное вершинам v4 и v3.
Вершина v1 инцидентна ребру e6.
Ребро (u, v) соединяет вершины u и v.
Дуга
Вершины v2 v3 и v4 соседи вершины v1
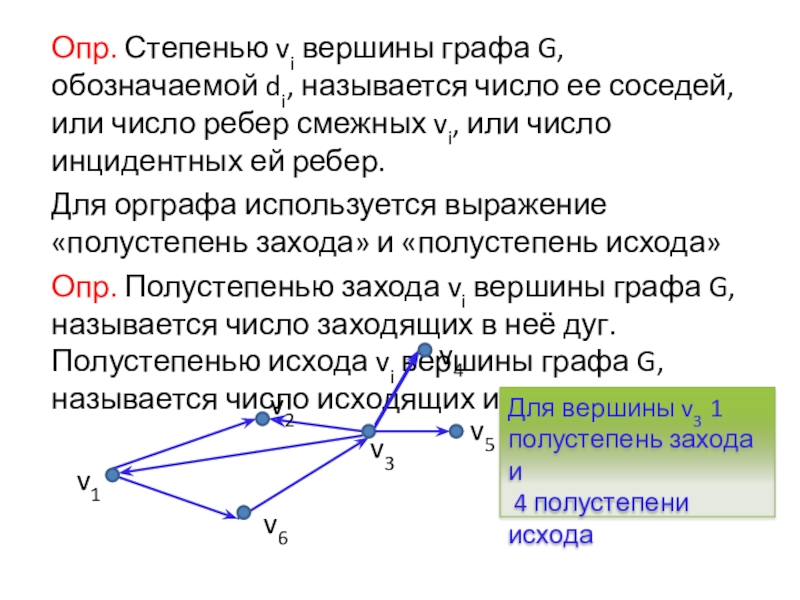
Слайд 10Опр. Степенью vi вершины графа G, обозначаемой di, называется число ее
Для орграфа используется выражение «полустепень захода» и «полустепень исхода»
Опр. Полустепенью захода vi вершины графа G, называется число заходящих в неё дуг. Полустепенью исхода vi вершины графа G, называется число исходящих из неё дуг.
v3
v6
v1
v2
v4
v5
Для вершины v3 1 полустепень захода и
4 полустепени исхода
Слайд 11Сумма полустепеней исходов (заходов) в орграфе G равно числу его ребер
Сумма степеней вершин неориентированного графа равна 2|Е|, где |Е| число ребер.
Вершина vi графа G называется изолированной, если ее степень di=0. Если степень di=1, то вершина называется концевой.
V2 (концевая)
V1 (изолированная)
v3
v4
v5
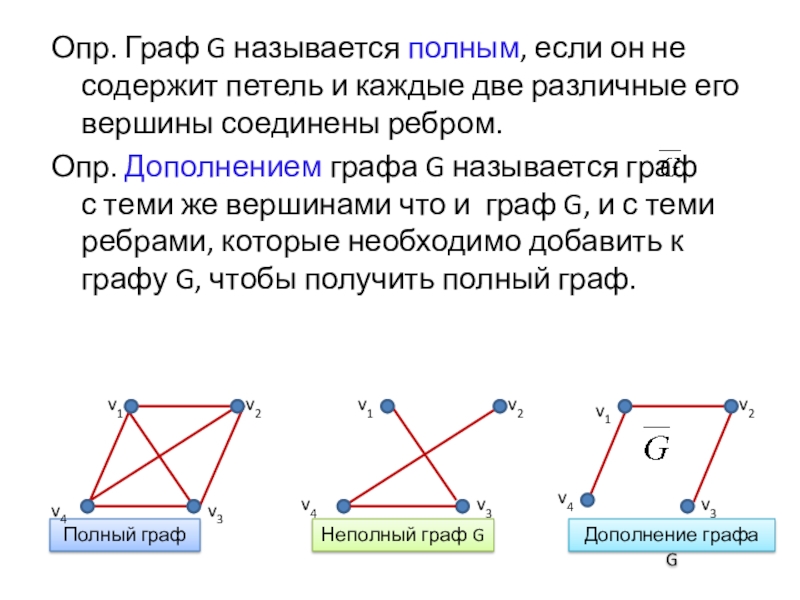
Слайд 12Опр. Граф G называется полным, если он не содержит петель и
Опр. Дополнением графа G называется граф с теми же вершинами что и граф G, и с теми ребрами, которые необходимо добавить к графу G, чтобы получить полный граф.
Полный граф
Неполный граф G
Дополнение графа G
v1
v2
v3
v4
v1
v2
v3
v4
v1
v2
v3
v4
Слайд 13Граф G={V,E} называется двудольным, если множество его вершин V можно разбить
Vα ={a,b,c,d}, Vα ={e,f,g,h},
Vβ ={m,n,p,q,s} Vβ ={x,r,t}
a
b
c
d
e
f
g
h
m
n
p
q
s
x
r
t
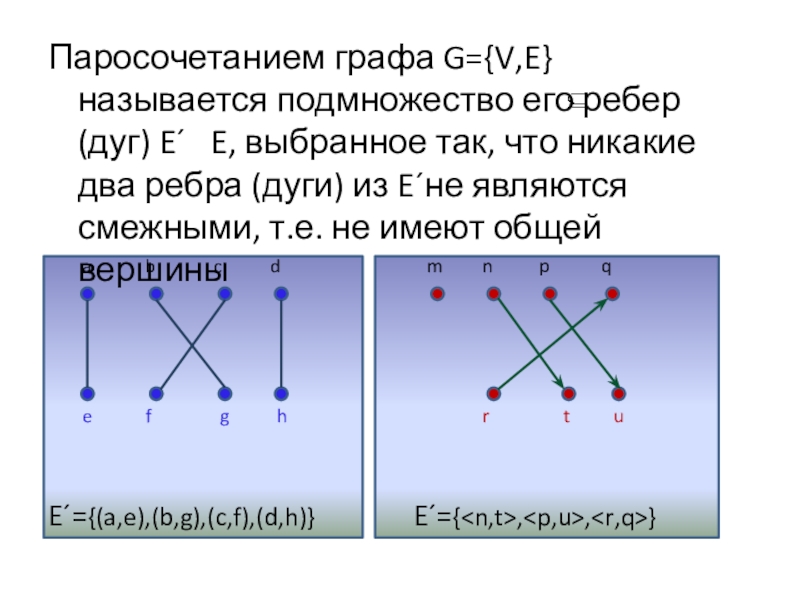
Слайд 14Паросочетанием графа G={V,E} называется подмножество его ребер (дуг) E´ E,
E´={(a,e),(b,g),(c,f),(d,h)} E´={
a
b
c
d
e
f
g
h
m
n
p
q
r
t
u
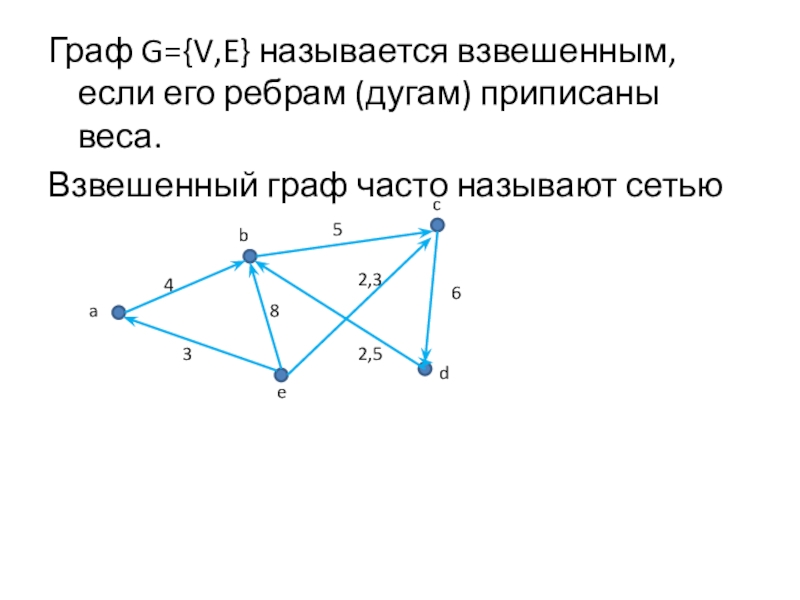
Слайд 15Граф G={V,E} называется взвешенным, если его ребрам (дугам) приписаны веса.
Взвешенный граф
a
b
c
d
e
4
5
6
2,3
2,5
8
3
Слайд 16a
b
g
j
f
e
d
c
2
6
1,5
1,2
1,1
6,5
2,5
2,5
0,8
2,0
3,1
0,8
5,5
2
1,2
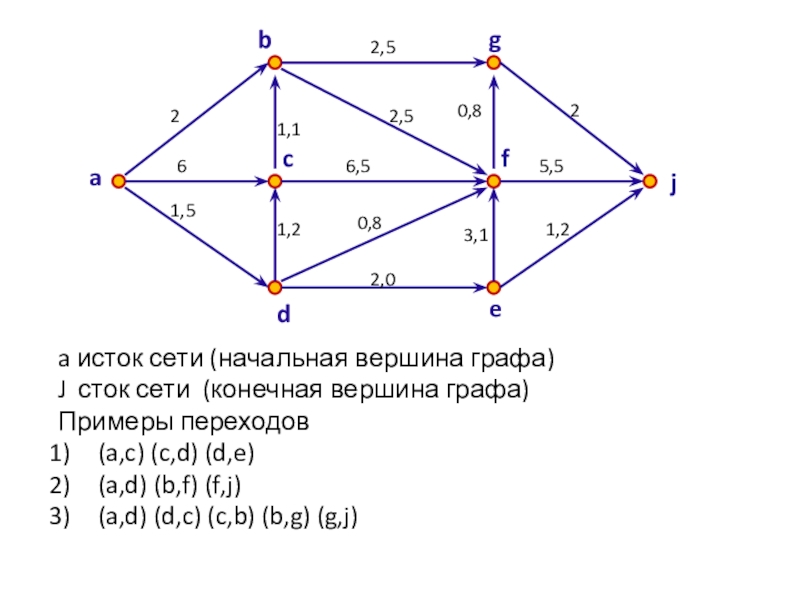
a исток сети (начальная вершина графа)
J сток сети (конечная вершина графа)
Примеры
(a,c) (c,d) (d,e)
(a,d) (b,f) (f,j)
(a,d) (d,c) (c,b) (b,g) (g,j)
Слайд 17Маршрутом в неориентированном графе G={V,E} называется такая последовательность ребер e1, e2,.
Записывается последовательностью вершин
a,c,f,j
a,d,c,b,f,g
d,c,f,e
Если первая и последняя вершина совпадают то маршрут называется циклическим.
Слайд 18Маршрут называется цепью, если каждое ребро графа (вершина) встречается в маршруте
Граф не содержащий циклов, называется ациклическим.
Для орграфа аналогом маршрута является путь.
Слайд 19Гамильтоновым циклом в графе G={V,E} называется цикл, проходящий через каждую вершину
Граф G={V,E}, содержащий гамильтоновый цикл, называется гамильтоновым графом.
Один из гамильтоновых
циклов 1,2,3,4
4
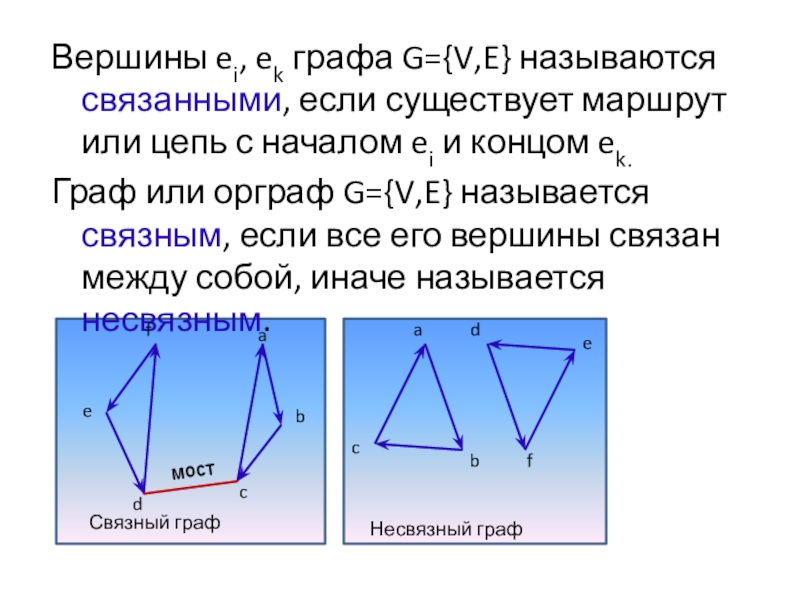
Слайд 20Вершины ei, ek графа G={V,E} называются связанными, если существует маршрут или
Граф или орграф G={V,E} называется связным, если все его вершины связан между собой, иначе называется несвязным.
f
e
d
c
b
a
Связный граф
Несвязный граф
мост
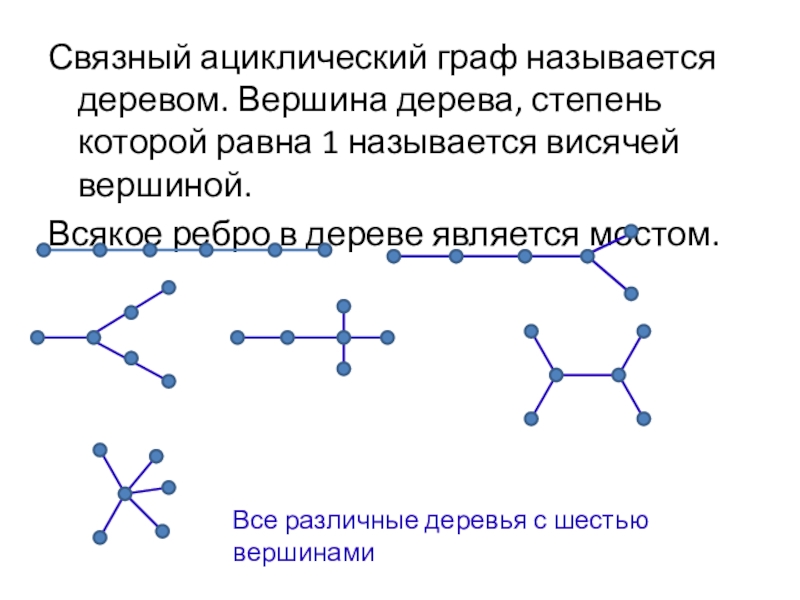
Слайд 21Связный ациклический граф называется деревом. Вершина дерева, степень которой равна 1
Всякое ребро в дереве является мостом.
Все различные деревья с шестью вершинами
Слайд 22Дерево, у которого одна вершина выделяется среди других , называется корневым
Неориентированное корневое дерево
Ориентированное корневое дерево