- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Особенности построения графиков функций, заданных неявно и параметрически
Содержание
- 1. Презентация: Особенности построения графиков функций, заданных неявно и параметрически
- 2. Алгоритм исследования графиков функций заданных явноОпределить область
- 3. Построить график функции
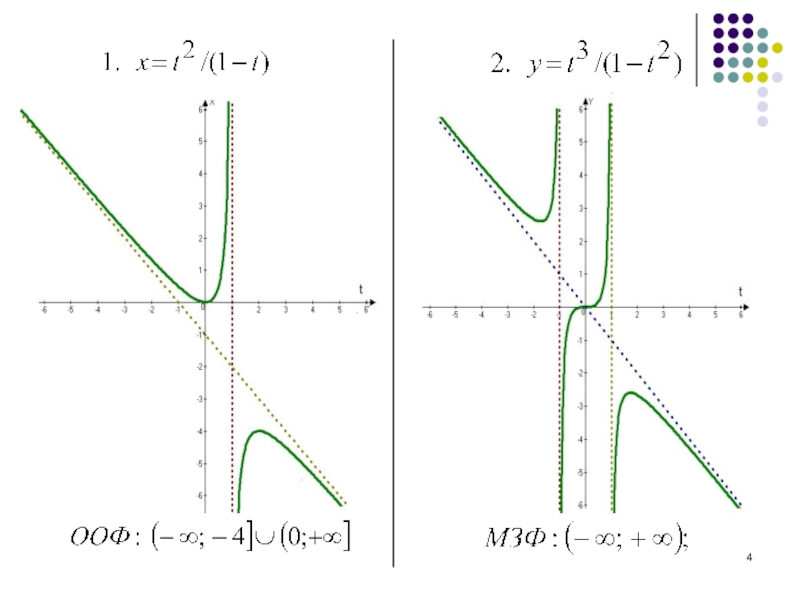
- 4. Слайд 4
- 5. 4. Особые точки:Точку
- 6. I. p- нечетное, q- четное – образ
- 7. III. p- четное,q - нечетное – точка
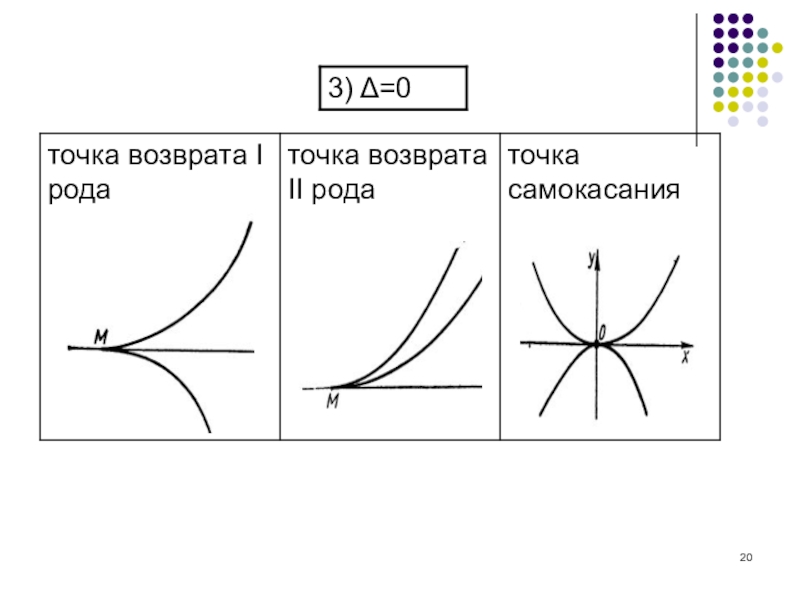
- 8. Таким образом, начало координат является точкой возврата I рода (p=2, q=3).
- 9. 5) Точки самопересечения:
- 10. 6) Угловой коэффициент касательной:
- 11. Экстремумы функции: (0;0)-т. min; (-4,1;-2,6) и (1,1;2,6)
- 12. 7) Интервалы выпуклости и точки перегиба:
- 13. Асимптоты.
- 14. Слайд 14
- 15. Исследовать и построить график функции 1) область
- 16. 3) Точки пересечения кривой с осями координат:
- 17. 4) Асимптоты: горизонтальных и вертикальных асимптот кривая
- 18. 5) Особые точки:Точка
- 19. Слайд 19
- 20. Слайд 20
- 21. Таким образом, (0;0) – особая (
- 22. 6) Координаты точек, в которых касательные параллельны
- 23. Т.к принимает положительные значения в точке
- 24. Координаты точек, в которых касательные параллельны оси
- 25. Т.к
- 26. Точки перегиба:
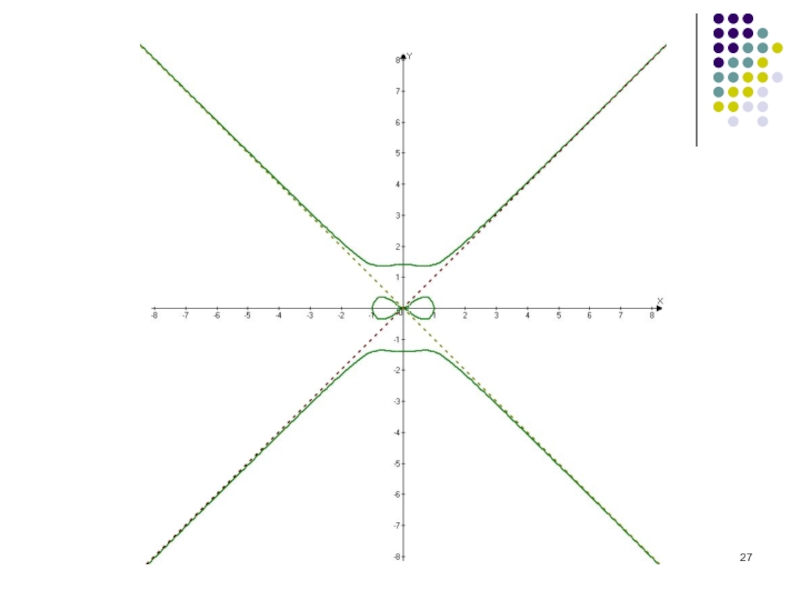
- 27. Слайд 27
- 28. Специфическая особенность - нахождение особых точек и
Слайд 1Тема: Особенности построения графиков функций заданных неявно и параметрически
Подготовила: Полякова Ольга
Слайд 2Алгоритм исследования графиков функций заданных явно
Определить область определения функции;
найти множество значений
определить четность (нечетность) функции;
определить периодичность функции;
найти нули функции;
найти экстремумы функции, определить промежутки монотонности функции;
определить выпуклость и точки перегиба.
найти асимптоты.
Слайд 54. Особые точки:
Точку
- первая отличная от нуля производная
- первая из производных, не коллинеарных вектору
Слайд 6I. p- нечетное, q- четное – образ кривой в окрестности точки
II. p- нечетное, q- нечетное – точка M
является точкой перегиба;
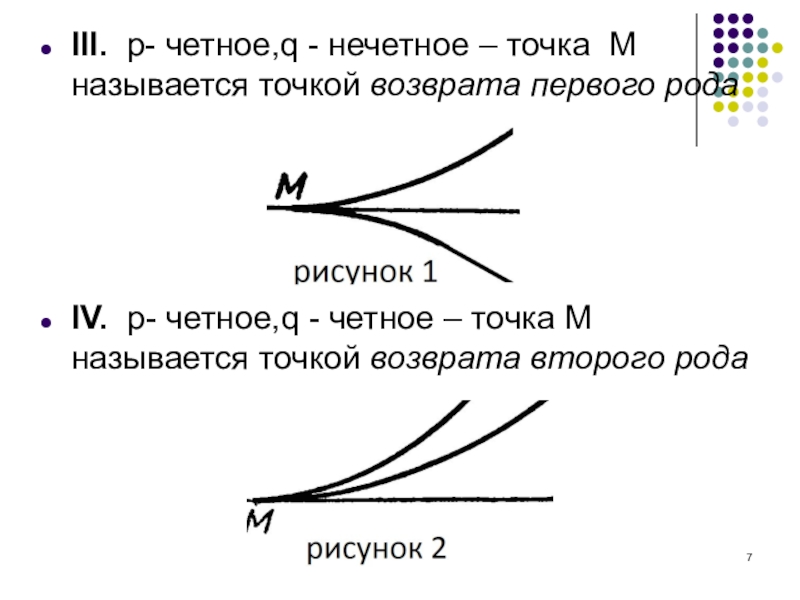
Слайд 7III. p- четное,q - нечетное – точка M называется точкой возврата
IV. p- четное,q - четное – точка M называется точкой возврата второго рода
Слайд 106) Угловой коэффициент касательной:
При t=0 и при t = (т. е. точках (0;0); (-4,1;-2,6) и (1,1; 2,6) ) касательная параллельна оси абсцисс;
при t=2 (т. е в точке(-4; -2,6) ) касательная параллельна оси ординат.
Слайд 11Экстремумы функции:
(0;0)-т. min; (-4,1;-2,6) и (1,1;2,6) – т. max
При
при и
функция возрастает
Слайд 127) Интервалы выпуклости и точки перегиба:
Точек перегиба кривая не имеет;
при и при кривая выпукла вверх;
при и при кривая выпукла вниз.
Слайд 13Асимптоты.
(5)
значит у=х+1 – наклонная асимптота,
при вертикальная асимптота;
при
(6), значит
наклонная асимптота;
горизонтальных асимптот функция не имеет.
Слайд 15Исследовать и построить график функции
1) область определения:
первой ветви
2) Кривая симметрична относительно координатных осей
Слайд 174) Асимптоты:
горизонтальных и вертикальных асимптот кривая не имеет.
наклонные асимптоты:
(9)
(10)
у=х и у=-х – наклонные асимптоты.
Слайд 185) Особые точки:
Точка кривой
(11)
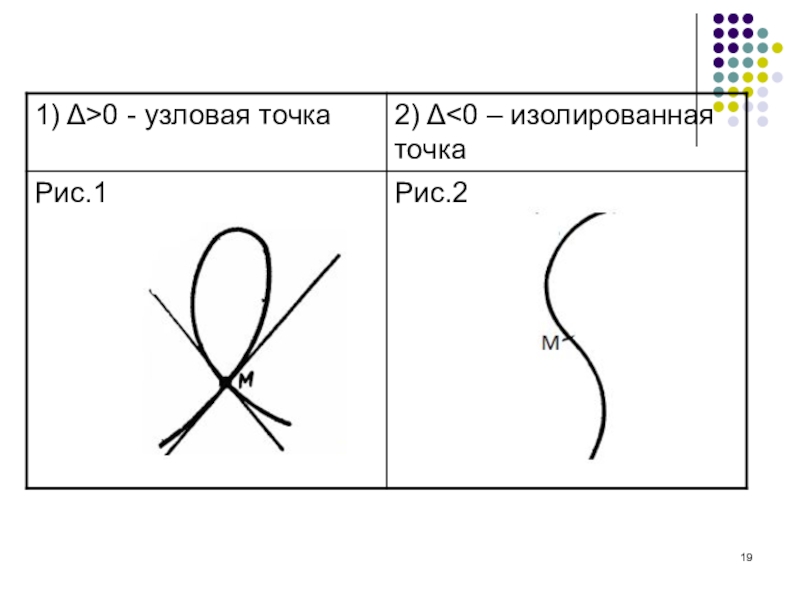
Если производные второго порядка не равны одновременно нулю в точке , тогда эта точка является двойной точкой кривой, причем форма кривой у ее двойной точки характеризуется значением:
(12)
Слайд 226) Координаты точек, в которых касательные параллельны оси абсцисс:
(0;0) , -в этих точках касательная параллельна оси абсцисс.
Слайд 23Т.к
принимает положительные значения в точке
т. к. (14) принимает отрицательные значения в точках , то в этих точках у-min.
(14)
Слайд 24Координаты точек, в которых касательные параллельны оси ординат:
(0:0), (1;0), (-1;0) - в этих точках касательные параллельны оси ординат
Слайд 25 Т.к
т. к. (16) принимает отрицательные значения в точке с координатами (-1;0), то в этой точке х-min.