- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Неравенства с одним неизвестным
Содержание
- 1. Презентация Неравенства с одним неизвестным
- 2. IIДва поезда вышли одновременно навстречу друг другу
- 3. х км/ч Пусть х километров
- 4. В неравенстве 4х ≥ 200 буквой х
- 5. Многие неравенства сводятся к линейным, например:Неизвестное число в неравенстве может бытьобозначено любой буквой, например в неравенствах
- 6. неизвестные обозначены соответственно буквамиy, t,
- 7. Назовите левую часть неравенстваНазовите правую часть неравенства
- 8. Если в неравенствоподставить а = 10,
- 9. Решением неравенства с одним неизвестным называется
- 10. Блиц-опросРешить неравенство :1) ─ 5 х <
- 11. 1 вариант4х(х–1)+(5х–1)(х+1)+1>–16,4х²– 4х+5х² +5х –х–1+1>–16,9х² > –16,что
- 12. Блиц-опросПостроен график функции у = k
- 13. Блиц-опросПостроен график функции С помощьюграфика заполнитьпропуски.2) Значения
Слайд 1Неравенства с одним неизвестным
Ш. А. Алимов, 8 класс
Методическая разработка :Жукова Т.В.
МОУ
Слайд 2II
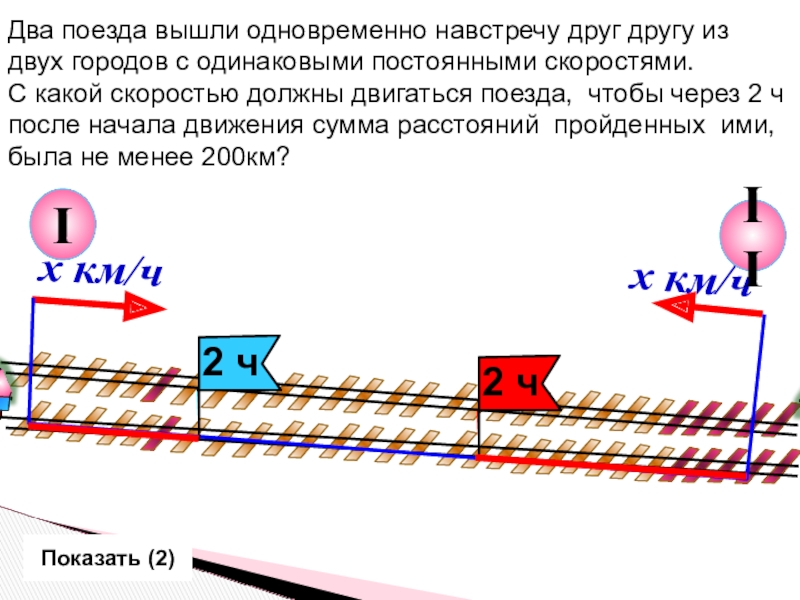
Два поезда вышли одновременно навстречу друг другу из
двух городов с
С какой скоростью должны двигаться поезда, чтобы через 2 ч
после начала движения сумма расстояний пройденных ими,
была не менее 200км?
I
х км/ч
Показать (2)
Слайд 3
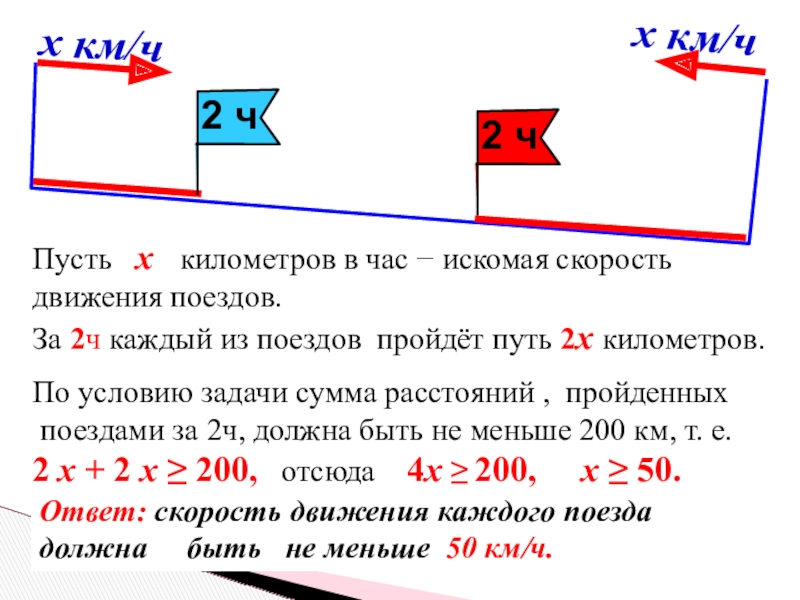
х км/ч
Пусть х километров в час − искомая
движения поездов.
За 2ч каждый из поездов пройдёт путь 2х километров.
По условию задачи сумма расстояний , пройденных
поездами за 2ч, должна быть не меньше 200 км, т. е.
2 х + 2 х ≥ 200, отсюда 4х ≥ 200, х ≥ 50.
Ответ: скорость движения каждого поезда должна быть не меньше 50 км/ч.
Слайд 4В неравенстве 4х ≥ 200 буквой х обозначено
неизвестное число.
Это пример
неизвестным.
Линейными неравенствами с одним неизвестным
называются неравенства вида:
a х > b,
a x < b,
a х ≥ b,
a x ≤ b,
где а и b − заданные числа, х − неизвестное.
Слайд 5Многие неравенства сводятся к линейным, например:
Неизвестное число в неравенстве может быть
обозначено
Слайд 6неизвестные обозначены соответственно буквами
y, t, a.
Выражения, стоящие слева и
неравенства, называют соответственно левой и
правой частями неравенства.
Каждое слагаемое левой и правой частей неравенства
называют членом неравенства.
Слайд 8Если в неравенство
подставить а = 10, а = 4,
числовые неравенства :
2∙ (5 − 2 ∙ 10) < 3 ∙ 10 + 2 ∙ (5 − 3 ∙ 10);
2∙ (5 − 2 ∙ 4) < 3 ∙ 4 + 2 ∙ (5 − 3 ∙ 4).
Каждое из чисел 10, 4 называют решением
неравенства
Слайд 9Решением неравенства с одним неизвестным
называется то значение неизвестного, при
это неравенство обращается в верное числовое
неравенство.
Решить неравенство − это значит найти все его
решения или установить, что их нет.
Из чисел 7; 5; 2; 1,5; 0; −2 выбрать те, которые
являются решениями неравенства :
1) 2 х − 3 ≥ 1;
2) 4 ─ х < 3;
3) 4 (х−1) < − 2;
4) 2 (1 − х ) ≥ −1;
Слайд 10Блиц-опрос
Решить неравенство :
1) ─ 5 х < 0, ______________
2)
3) ─ 0,5 х ² ─ 1 < 0, ___________________________
4) ( х ─ 3 ) ² < 0, ____________________________
5) ( х + 2 ) ² > 0,
___________________________________________
Слайд 111 вариант
4х(х–1)+(5х–1)(х+1)+1>–16,
4х²– 4х+5х² +5х –х–1+1>–16,
9х² > –16,
что верно при любом
значении
2 вариант
(х – 4)(х+4) – 2 х² <1,
х² –16 – 2х² <1,
– х² –16 <1,
что верно при любом
значении х.
Доказать, что при любом х справедливо неравенство:
Слайд 12Блиц-опрос
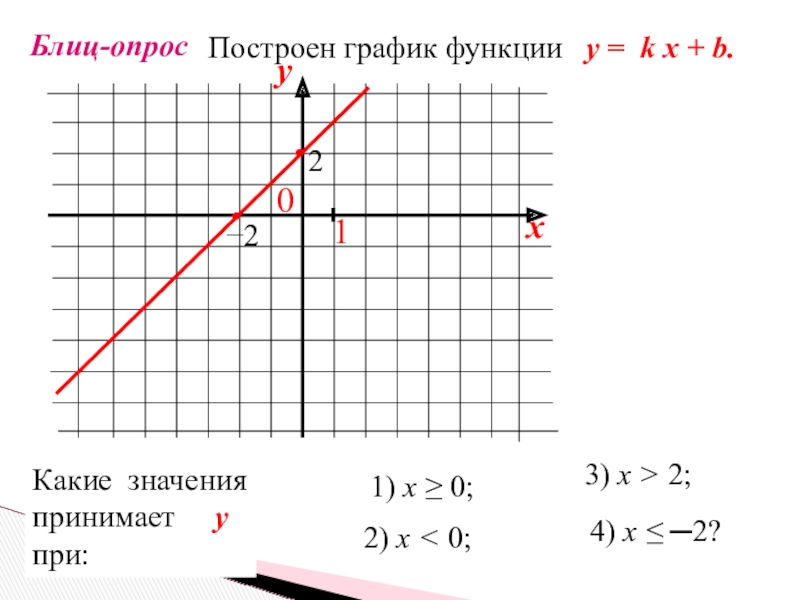
Построен график функции у = k x + b.
Какие
при:
2) х < 0;
1) х ≥ 0;
3) х > 2;
4) х ≤ ─2?
−2
2
•
•
1
0
у
х
Слайд 13Блиц-опрос
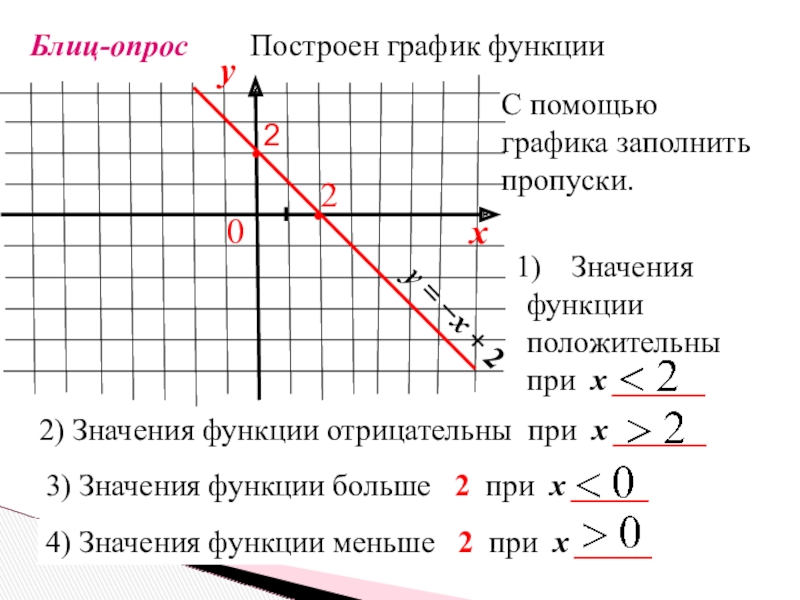
Построен график функции
С помощью
графика заполнить
пропуски.
2) Значения функции отрицательны при х
Значения
функции
положительны
при х ______
3) Значения функции больше 2 при х _____
4) Значения функции меньше 2 при х _____
2
•
•
2
0
у
х
у = −х + 2