- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на НПК по теме :Магические квадраты
Содержание
- 1. Презентация на НПК по теме :Магические квадраты
- 2. ВведениеЧеловек различает окружающие его предметы по форме.
- 3. Еще в эпоху Возрождения художники открыли, что
- 4. Слайд 4
- 5. Построение золотого сеченияПрактическое знакомство с золотым сечением
- 6. Полученная при этом точка Е делит отрезок
- 7. Слайд 7
- 8. Построение второго золотого сеченияБолгарский журнал «Отечество» (№10,
- 9. Деление осуществляется следующим образом. Отрезок АВ делится
- 10. Слайд 10
- 11. Построение пентаграммы Для построения пентаграммы
- 12. Каждый конец пятиугольной звезды представляет
- 13. Золотое сечение в природе Раковина закручена
- 14. Слайд 14
- 15. Среди придорожных трав растет ничем не примечательное
- 16. В ящерице с первого взгляда улавливаются приятные
- 17. И в растительном, и в животном мире
ВведениеЧеловек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему
Слайд 2Введение
Человек различает окружающие его предметы по форме. Интерес к форме какого-либо
предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.
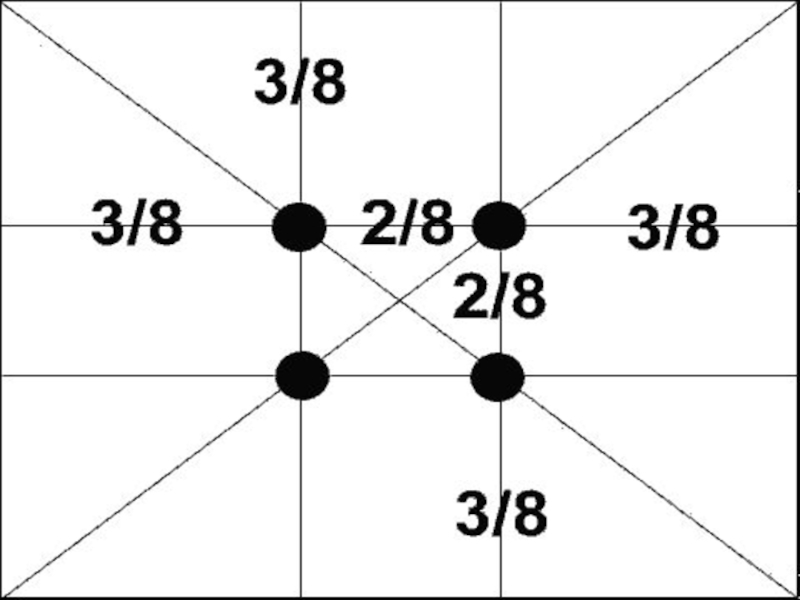
Слайд 3Еще в эпоху Возрождения художники открыли, что любая картина имеет определенные
точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, какой формат имеет картина - горизонтальный или вертикальный. Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости.
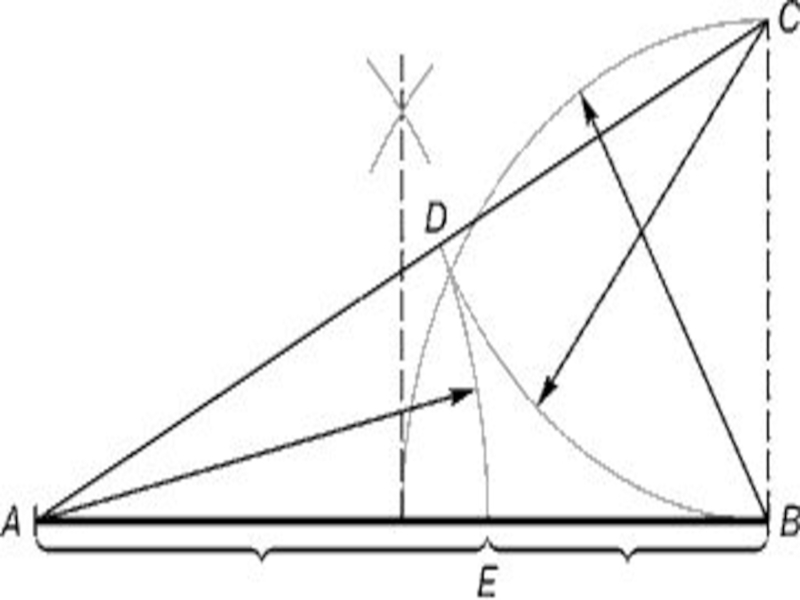
Слайд 5Построение золотого сечения
Практическое знакомство с золотым сечением начинают с деления отрезка
прямой в золотой пропорции с помощью циркуля и линейки.
Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ.
Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ.
Слайд 6Полученная при этом точка Е делит отрезок АВ в соотношении золотой
пропорции.Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE= 0,618..., если АВ принять за единицу, ВЕ= 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.
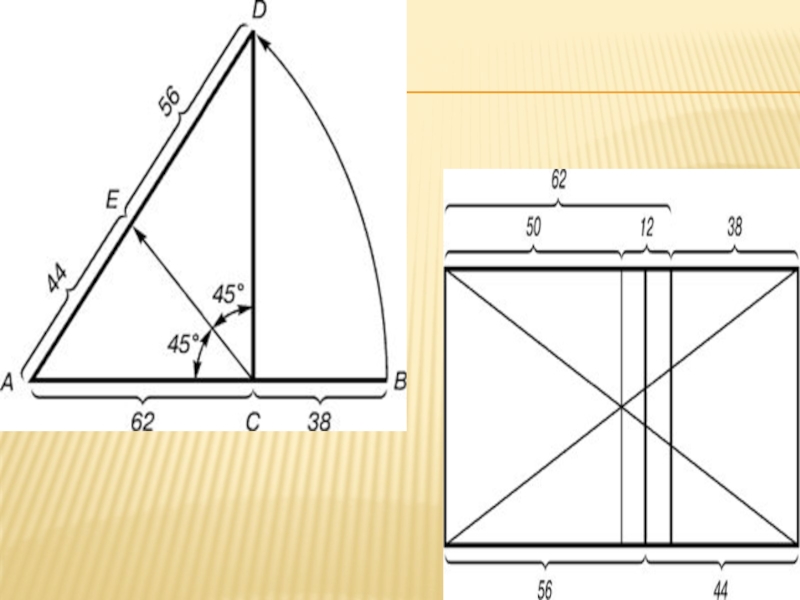
Слайд 8Построение второго золотого сечения
Болгарский журнал «Отечество» (№10, 1983 г.) опубликовал статью Цветана
Цекова-Карандаша «О втором золотом сечении», которое вытекает из основного сечения и дает другое отношение 44 : 56.
Такая пропорция обнаружена в архитектуре, а также имеет место при построении композиций изображений удлиненного горизонтального формата.
Такая пропорция обнаружена в архитектуре, а также имеет место при построении композиций изображений удлиненного горизонтального формата.
Слайд 9Деление осуществляется следующим образом. Отрезок АВ делится в пропорции золотого сечения.
Из точки С восставляется перпендикуляр СD. Радиусом АВ находится точка D, которая соединяется линией с точкой А. Прямой угол АСD делится пополам. Из точки С проводится линия до пересечения с линией AD. Точка Е делит отрезок AD в отношении 56 : 44.
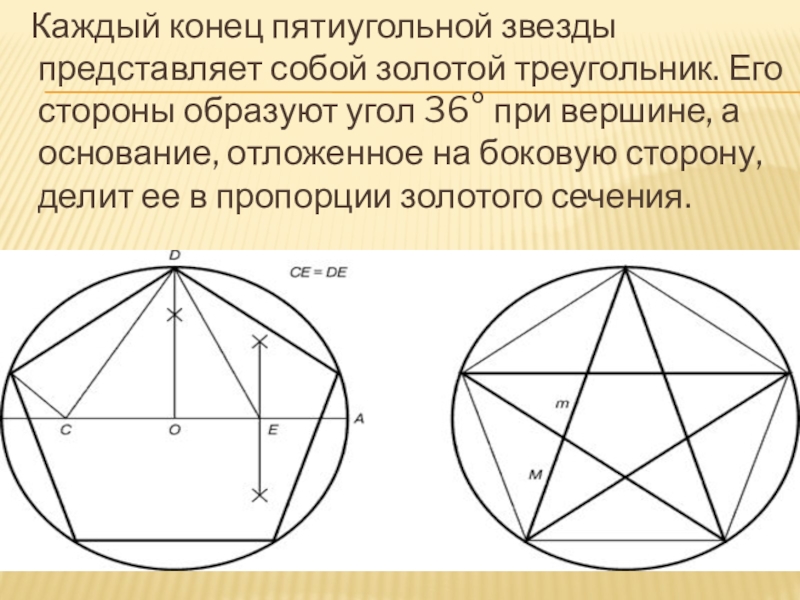
Слайд 11Построение пентаграммы
Для построения пентаграммы необходимо построить правильный пятиугольник.
Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471...1528). Пусть O – центр окружности, A – точка на окружности и Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Слайд 12 Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его
стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
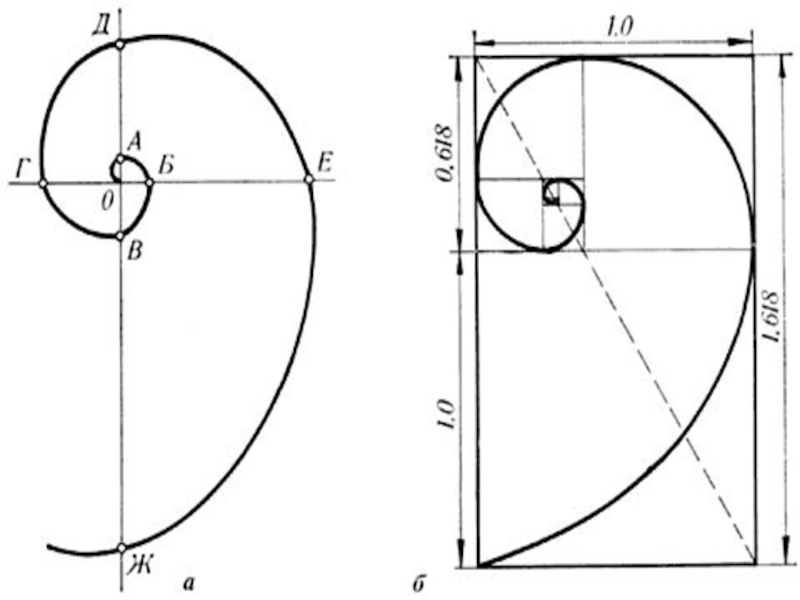
Слайд 13Золотое сечение в природе
Раковина закручена по спирали. Если ее
развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Спирали очень распространены в природе. Представление о золотом сечении будет неполным, если не сказать о спирали.
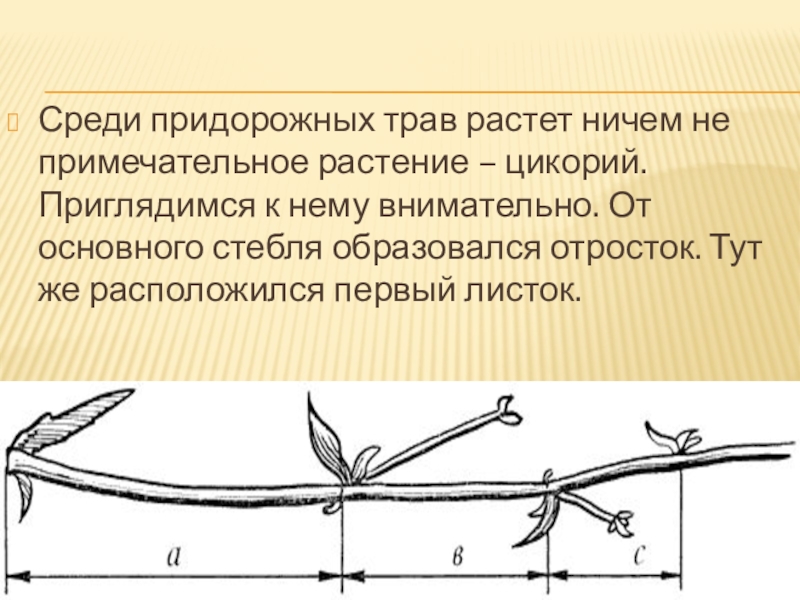
Слайд 15Среди придорожных трав растет ничем не примечательное растение – цикорий. Приглядимся
к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок.
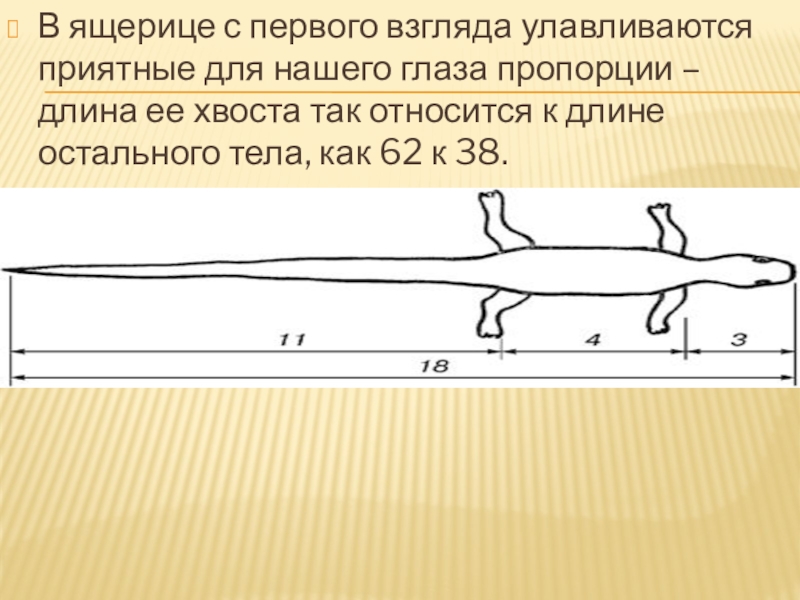
Слайд 16В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции
– длина ее хвоста так относится к длине остального тела, как 62 к 38.
Слайд 17И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция
природы – симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста.
Конец