- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Множества и операции над ними.
Содержание
- 1. Презентация Множества и операции над ними.
- 2. Знаменитый итальянский физик, механик, астроном и математик
- 3. При изучении параграфа «Множества и
- 4. Понятие теории множеств Понятие множества является
- 5. Объекты, составляющие множество, называются элементами множества.
- 6. Множество состоит из элементов. Если
- 7. Множества, элементами которых являются числа, называются числовыми
- 8. Способы задания множеств
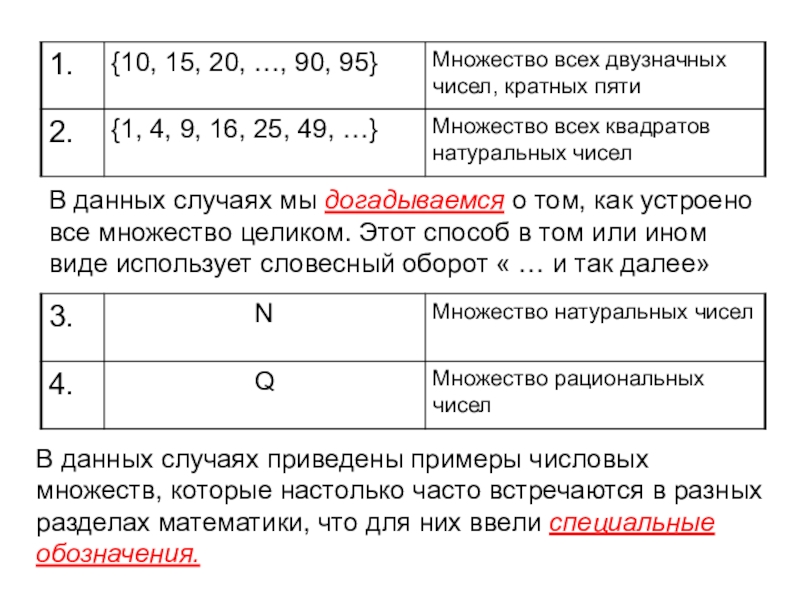
- 9. В данных случаях мы догадываемся о том,
- 10. В случае 5 множество задано с помощью его характеристического свойства (самый распространенный способ)Чтение записи
- 11. Пример 2По указанному заданию множества дать его
- 12. Пример 3Решив соответствующее неравенство, составить более привычную
- 13. принадлежитне принадлежитПримеры:3 {1, 3, 5, 7, 9}13 {1, 3, 5, 7, 9}
- 14. Элементы, образующие множество А, можно
- 15. Решение:А = {х, у, z, t} –
- 16. Сведения о четырехэлементном множествеВсего : 1 +
- 17. Определение подмножества:Если каждый элемент множества В является
- 18. Изображение множеств в виде плоских фигур очень
- 19. Операции над множествамиПересечение множествОбъединение множествПересечением множеств А
- 20. Пример. Найти пересечение множеств А и В:
- 21. Можно рассматривать пересечения не только двух множеств,
- 22. Пример. Найти объединение множеств А и В.
- 23. Можно рассматривать объединения не только двух, но
- 24. Домашнее задание:1. §17 № 533, 537, 540, 542, 544
Слайд 2Знаменитый итальянский физик, механик, астроном и математик Галилео Галилей (1564-1642) писал,
Слайд 3 При изучении параграфа «Множества и операции над ними» вы
элемент множества;
подмножество данного множества;
объединение множеств;
пересечение множеств.
Слайд 4Понятие теории множеств
Понятие множества является одним из наиболее общих
Множество- совокупность объектов, обладающих определенным свойством, объединенных в единое целое.
Слайд 5 Объекты, составляющие множество, называются элементами множества.
Среди множеств выделяют особое
Пустое множество- множество, не содержащее ни одного элемента.
Пустое множество является частью любого множества.
№3. Примеры пустых множеств. Решение:
1) Множество квадратных уравнений, которые имеют более двух разных корней;
2) множество простых делителей числа 1;
3) множество точек пересечения двух параллельных прямых;
4) множество прямых углов равностороннего треугольника;
5) множество людей на Солнце;
6) множество двузначных положительных чисел, расположенных на числовом луче левее 9.
Слайд 6 Множество состоит из элементов. Если этих элементов немного, то
Слайд 7Множества, элементами которых являются числа, называются числовыми множествами.
Множество А состоит из
Решить это уравнение.
Задать множество А перечислением его элементов.
Записать все возможные способы перечисления элементов множества А.
Сколько всего имеется способов перечисления элементов множества А?
Решение:
х3 + х2 – 6х = 0
х(х2 + х – 6) = 0
х(х + 3)(х – 2) = 0
х=0; х=-3; х=2
2)А={-3; 0; 2}
3) {-3; 0; 2} , {-3; 2; 0},
{0; 2; -3}, {0; -3; 2},
{2; -3; 0}, {2; 0; -3}
4) 6
Пример 1
Слайд 9В данных случаях мы догадываемся о том, как устроено все множество
В данных случаях приведены примеры числовых множеств, которые настолько часто встречаются в разных разделах математики, что для них ввели специальные обозначения.
Слайд 10 В случае 5 множество задано с помощью его характеристического
Чтение записи
Слайд 11Пример 2
По указанному заданию множества дать его словесное описание:
а) {0, 2,
б) {2, 4, 6, … 18, 20}
в) {12, 22, 32, … 92}
г) {1, 8, 27, 64, 125, …}
Множество всех четных цифр (все цифры, кроме 1,3,5,7,9)
Множество всех четных натуральных чисел, которые меньше 21
( все числа, полученные из чисел 1, 2, … 9, 10 умножением на 2)
Множество всех двузначных чисел, оканчивающихся на 2
Множество всех кубов натуральных чисел
Слайд 12Пример 3
Решив соответствующее неравенство, составить более привычную запись числового множества:
а) {х
г) {х | 35х2 < 24x +35}
Ответы:
а) (-∞; +∞) или R
б) Ø (пустое множество)
в) (0; 1)
г) [-5/7; 7/5]
Слайд 14 Элементы, образующие множество А, можно объединять не сразу все
Пример 4.
На поле в составе футбольной команды должны выйти два нападающих, а у тренера команды есть четыре кандидата х, у, z, t на эти позиции.
а) Из скольких вариантов придется выбирать тренеру?
б) Как изменится ответ в а), если игрок х не может играть с игроком у?
в) Как изменится ответ в а), если игрок z может играть только вместе с игроком t?
г) Как изменится ответ в а), если на поле должны выйти три нападающих?
Слайд 15Решение:
А = {х, у, z, t} – это множество, из которого
а) Для игрока х: {х, у}, {х, z}, {х, t}
Для игрока у: {у, z}, {у, t}, вариант {х, у} – уже учтен.
Для игрока z: {z, t}, варианты {х, z}, {у, z} –уже учтены.
Для игрока t все варианты выхода на игру уже указаны
Ответ: 6 вариантов: {х, у}, {х, z}, {х, t}, {у, z}, {у, t}, {z, t}
б)из перечисленных вариантов следует убрать {х, у}.Ответ: 5 вариантов
в) из а) следует убрать: {х, z}, {у, z}. Ответ: 4 варианта
г) считаем все трехэлементные подмножества:
{х, у, z}, {х, у, t}, {х, z, t}, {у, z, t} Ответ: 4 варианта
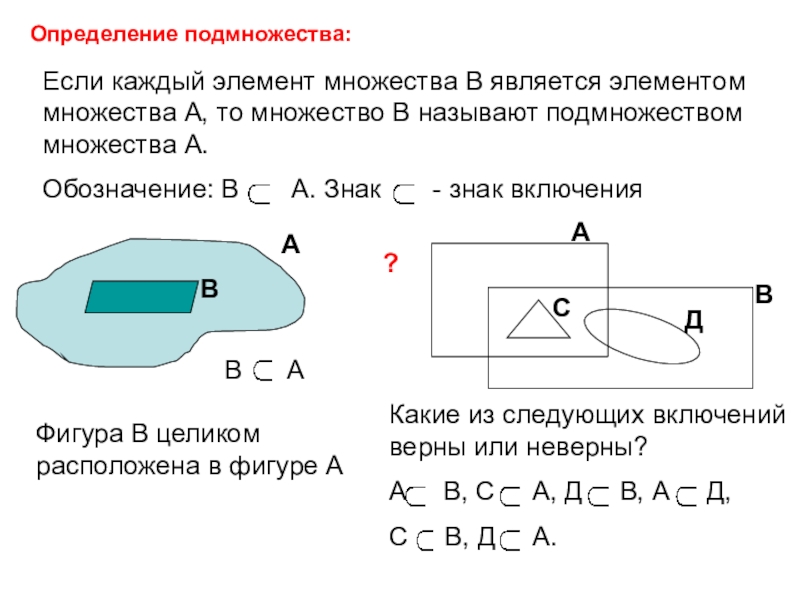
Слайд 17Определение подмножества:
Если каждый элемент множества В является элементом множества А, то
Обозначение: В А. Знак - знак включения
А
В
В А
Фигура В целиком расположена в фигуре А
А
В
С
Д
Какие из следующих включений верны или неверны?
А В, С А, Д В, А Д,
С В, Д А.
?
Слайд 18Изображение множеств в виде плоских фигур очень удобно для наглядного объяснения
А – подмножество В
Слайд 19
Операции над множествами
Пересечение множеств
Объединение множеств
Пересечением множеств А и В называют множество,
Обозначение:
={х | х А и х В}
Круги Эйлера
Объединением множеств А и В называют множество, состоящее из всех элементов, которые принадлежат хотя бы одному из множеств – или множеству А, или множеству В.
Обозначение:
= {х | х А или х В}
Круги Эйлера
{1,2,3} {2,3,4} = {1,2,3,4}.
{1,2,3} {2,3,4} = {2,3}
Слайд 20Пример. Найти пересечение множеств А и В:
а) А = {11,
б) А – множество различных букв, используемых в слове «перераспределение», В – множество различных букв, используемых в слове « реформирование»
в) А = ( 1, √10), В = N;
г) А – множество точек окружности радиуса 1 с центром в начале координат, В – множество точек прямой у = 3х – 5.
Ответ:
а) А∩В = {33, 66, 99}
б) А∩В = {е, р, а, н, и}
в) А∩В = {2, 3}
г) А∩В = Ø
Слайд 21Можно рассматривать пересечения не только двух множеств, но и трех, четырех
Пересечением множеств А, В и С называют множество, состоящее из всех элементов, которые принадлежат и множеству А, и множеству В, и множеству С.
Пересечение множеств А, В и С обозначают так: А∩В∩С.
Пример выполнения нескольких условий : решение системы уравнений.
Слайд 22Пример. Найти объединение множеств А и В.
а) А – множество
б) А – множество цифр числа 35, в – множество цифр числа 210;
в) А = (1; √10), В = [ 2, 4];
г) А – множество точек координатной плоскости, у которых абсцисса больше 3, В – множество точек координатной плоскости, у которых ордината не больше 2.
Ответ:
а) АUВ = {1, 3, 5, 7, 11, 15, 21, 35, 55, 105}
б) АUВ = {0, 1, 2, 3, 4}
в) АUВ = (1,; 4]
Слайд 23Можно рассматривать объединения не только двух, но и трех, четырех и
Объединением множеств А, В, С называют множество, состоящее из всех элементов, которые принадлежат или множеству А, или множеству В, или множеству С.
Объединение множеств А, В, С обозначают так: АUВUС
Пример: решение неравенств