- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Многогранники вокруг нас
Содержание
- 1. Презентация Многогранники вокруг нас
- 2. Цель:Познакомиться с многогранным миром геометрии.
- 3. Задачи:Познакомиться с историей изучения многогранников.Уточнить представление о
- 4. Математика владеет не только истиной, но и
- 5. Названия многогранников пришли из Древней Греции и
- 6. МногогранникиОднородные выпуклыеОднородные
- 7. Правильными многогранниками Называют выпуклые многогранники, все грани
- 8. Правильные многогранникиСколько же их существует? Тетраэдр
- 9. Правильные многогранники Октаэдр – правильный четырёхугольный диэдр с равными рёбрами, ограниченный восемью правильными треугольниками.
- 10. Икосаэдр- поверхность, ограниченная двадцатью правильными треугольниками.Правильные многогранники
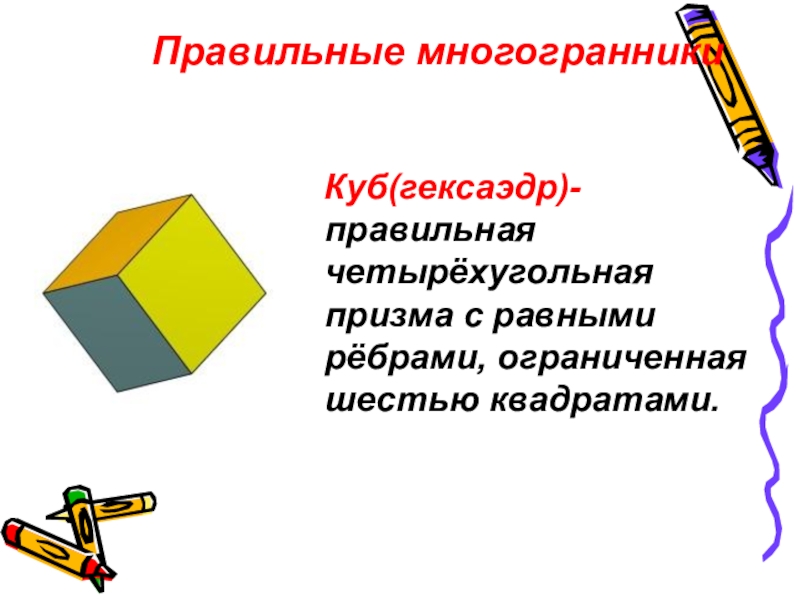
- 11. Куб(гексаэдр)- правильная четырёхугольная призма с равными рёбрами, ограниченная шестью квадратами.Правильные многогранники
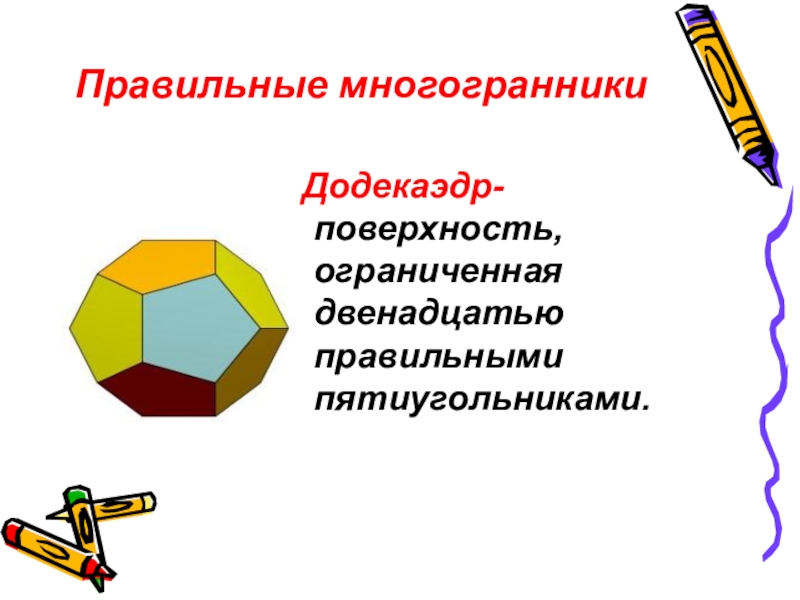
- 12. Правильные многогранники Додекаэдр- поверхность, ограниченная двенадцатью правильными пятиугольниками.
- 13. ТетраэдрГексаэдрДодекаэдрОктаэдрИкосаэдр
- 14. Сделаем вывод:Мы убедились, что существует лишь пять
- 15. водаземлявоздухогоньВселеннаядодекаэдргексаэдроктаэдрикосаэдртетраэдр Платон считал, что мир строится
- 16. Число вершин минус число ребер плюс число
- 17. Слайд 17
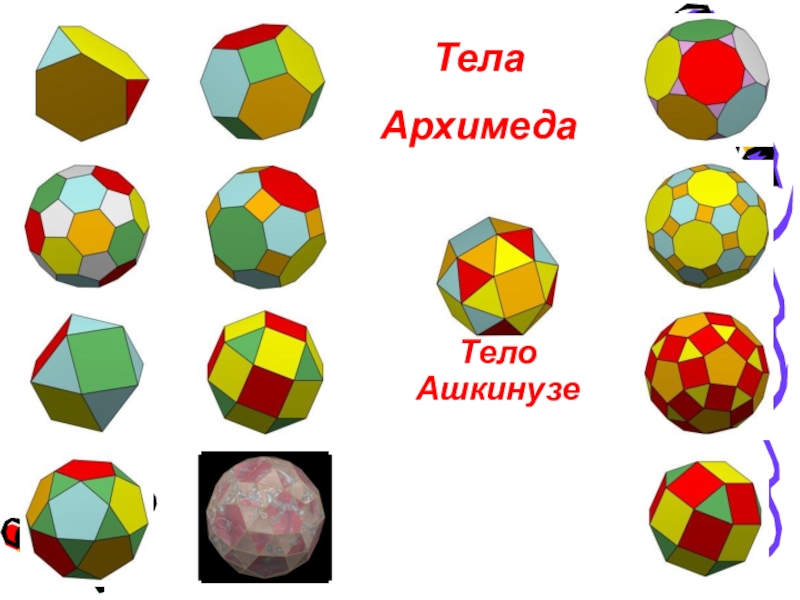
- 18. Тела АрхимедаАрхимедовыми телами называются полуправильные однородные выпуклые
- 19. Тела АрхимедаТелоАшкинузе
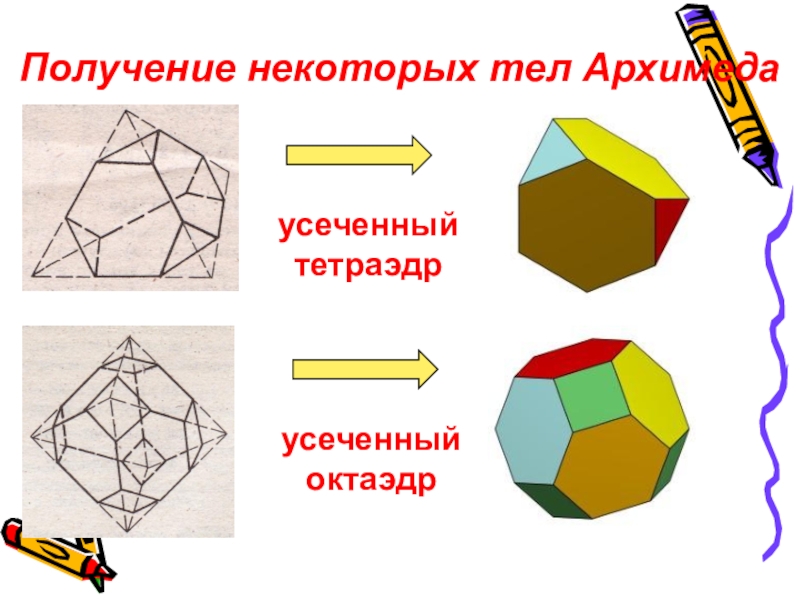
- 20. Получение некоторых тел Архимедаусеченный тетраэдрусеченный октаэдр
- 21. Архимед (287-211 гг. до н.э.)
- 22. Тела Кеплера – Пуансо (правильные звездчатые многогранники)
- 23. Большой звездчатыйдодекаэдрБольшой икосаэдрМалый звездчатыйдодекаэдрБольшой додекаэдр
- 24. Получение тел Кеплера - ПуансоПродолжение рёбер додекаэдра
- 25. Иоганн Кеплер предположил, что существует связь между
- 26. Иоганн Кеплер (1571-1630)
- 27. Снежинки – звёздчатые многогранникиА вы видели тени
- 28. Скелет одноклеточного организма феодарии по форме напоминает
- 29. : «Мой дом построен по законам самой
- 30. Многогранники – самые выгодные фигуры. И природа
- 31. Получение серной кислоты, железа, особых сортов цемента
- 32. Кристаллы Халькопирит Топаз
- 33. Многогранники в геологииИкосаэдро-додекаэдрическаяструктура Земли.
- 34. Многогранники в ювелирном деле
- 35. Многогранники в архитектуре и искусстве
- 36. Сальвадор Дали на картине «Тайная вечеря» изобразил
- 37. Вывод:благодаря многогранникам открываются не только удивительные свойства геометрических фигур, но и пути познания природной гармонии.
Слайд 3Задачи:
Познакомиться с историей изучения многогранников.
Уточнить представление о геометрическом строении многогранников, их
Существует ли связь между математической теорией и реальным миром, различными сферами жизни и деятельности человека, общества.
Слайд 4Математика владеет не только истиной, но и высшей красотой - красотой
Бертран Рассел
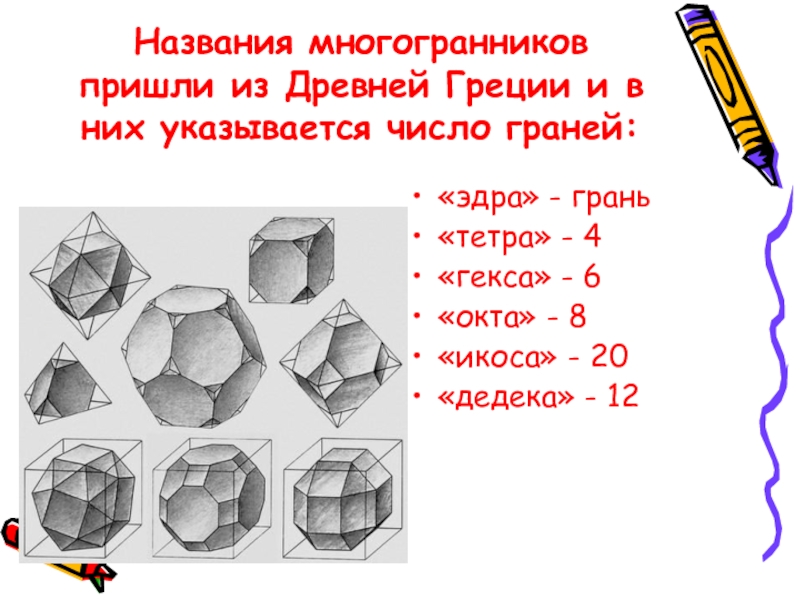
Слайд 5Названия многогранников пришли из Древней Греции и в них указывается число
«эдра» - грань
«тетра» - 4
«гекса» - 6
«окта» - 8
«икоса» - 20
«дедека» - 12
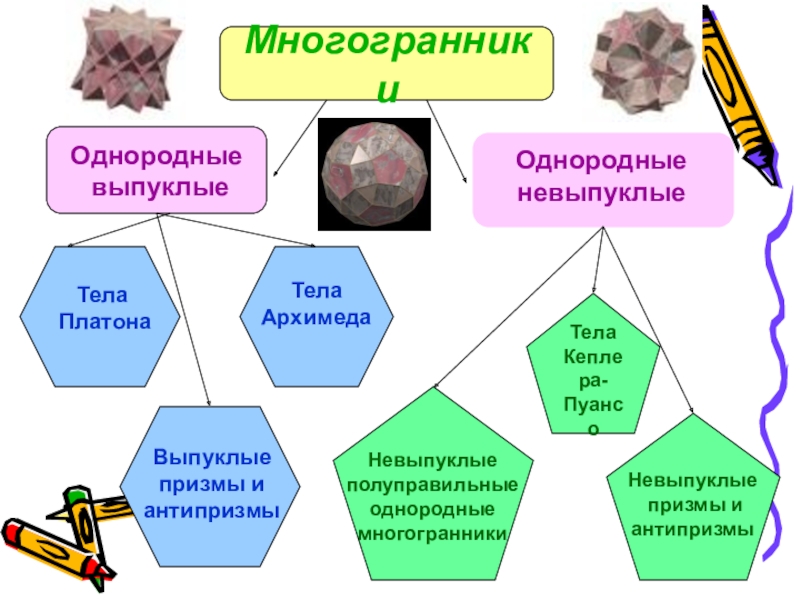
Слайд 6Многогранники
Однородные
выпуклые
Однородные
Тела
Архимеда
Тела
Платона
Выпуклые
призмы и
антипризмы
Тела
Кеплера-
Пуансо
Невыпуклые
полуправильные
однородные
многогранники
Невыпуклые
призмы и
антипризмы
Слайд 7Правильными многогранниками
Называют выпуклые многогранники, все грани и все углы которых
В каждой вершине правильного многогранника сходится одно и то же число рёбер.
Все двугранные углы при рёбрах и все многогранные углы при вершинах правильного многоугольника равны.
Правильные многогранники - трёхмерный аналог плоских правильных многоугольников.
Слайд 8Правильные многогранники
Сколько же их существует?
Тетраэдр -правильная треугольная пирамида с
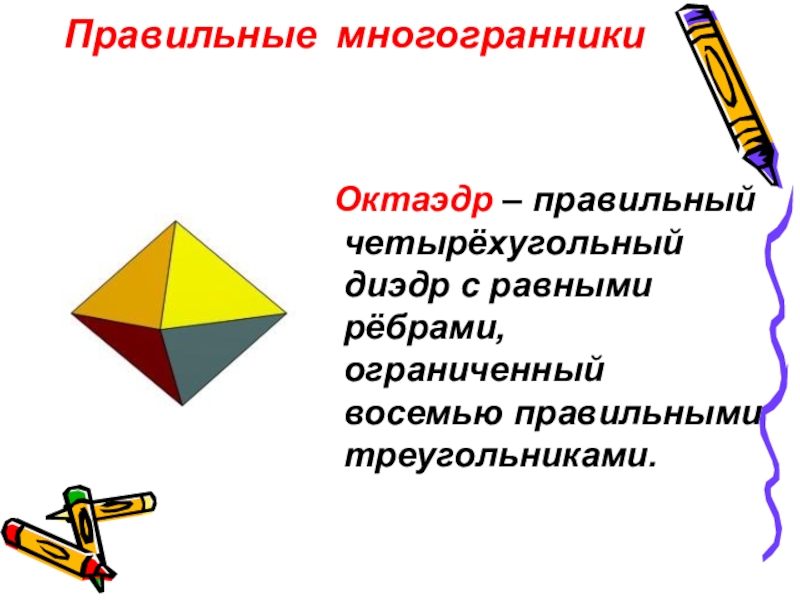
Слайд 9Правильные многогранники
Октаэдр – правильный четырёхугольный диэдр с равными рёбрами, ограниченный
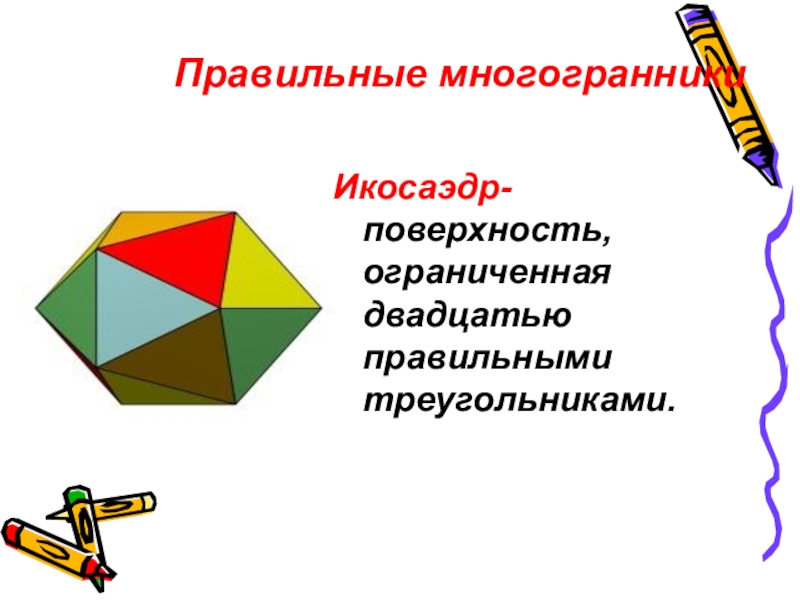
Слайд 10Икосаэдр- поверхность, ограниченная двадцатью правильными треугольниками.
Правильные многогранники
Слайд 11
Куб(гексаэдр)- правильная четырёхугольная призма с равными рёбрами, ограниченная шестью
Правильные многогранники
Слайд 12Правильные многогранники
Додекаэдр- поверхность, ограниченная двенадцатью правильными пятиугольниками.
Слайд 14Сделаем вывод:
Мы убедились, что существует лишь пять выпуклых правильных многогранников -
куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными
гранями.
Эти тела еще называют
телами Платона.
Слайд 15вода
земля
воздух
огонь
Вселенная
додекаэдр
гексаэдр
октаэдр
икосаэдр
тетраэдр
Платон считал, что мир строится из четырёх «стихий» -
Слайд 18Тела Архимеда
Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые
Слайд 24Получение тел Кеплера - Пуансо
Продолжение рёбер додекаэдра приводит к замене каждой
На продолжении граней додекаэдра возможны следующие два случая:
если рассматривать правильные пятиугольники, то получается большой додекаэдр;
если же в качестве граней рассматривать звёздчатые пятиугольники, то получается большой звёздчатый додекаэдр.
При продолжении граней правильного икосаэдра получается большой икосаэдр.
Слайд 25Иоганн Кеплер предположил, что существует связь между пятью правильными многогранниками и
Такая модель Солнечной системы получила название «Космического кубка» Кеплера. Результаты своих вычислений учёный опубликовал в книге «Тайна мироздания». Он считал, что тайна Вселенной раскрыта.
«Кубок Кеплера»
Слайд 27Снежинки – звёздчатые многогранники
А вы видели тени от снежинок?
А вы знаете,
В лунном блеске голубом и чистом
Или просто в свете фонаря?
Слайд 28Скелет одноклеточного организма феодарии по форме напоминает икосаэдр . Из
Многогранники
и природа
Слайд 29: «Мой дом построен по законам самой строгой архитектуры.
Сам Евклид
Слайд 30Многогранники – самые выгодные фигуры. И природа этим широко пользуется. Подтверждением
При производстве алюминия пользуются алюминиево-калиевыми кварцами , монокристалл которых имеет форму правильного октаэдра
Слайд 31Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого
В разных химических реакциях применяется сурьменистый сернокислый натрий – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра.
Слайд 36Сальвадор Дали на картине «Тайная вечеря» изобразил И. Христа со своими
"Тайнaя вечеря" С. Дали