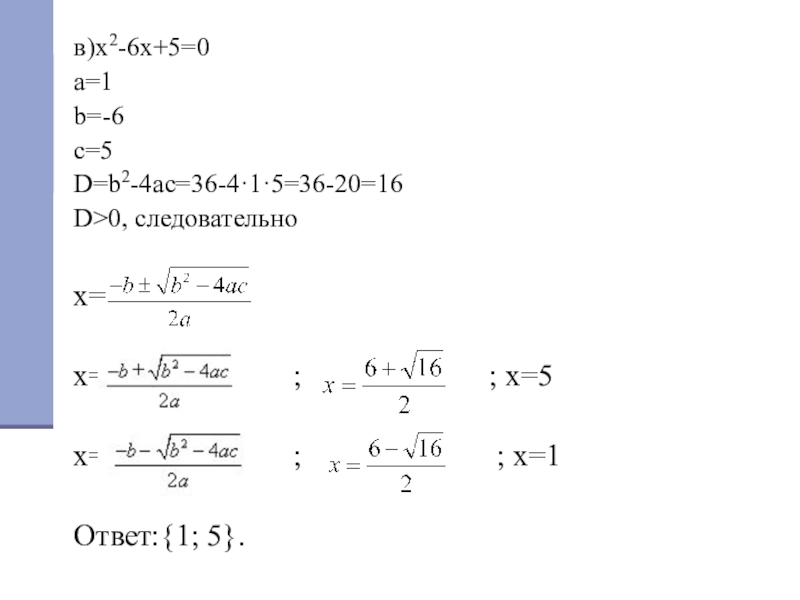- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад - Методическая разработка по теме Способы решения алгебраических уравнений.
Содержание
- 1. Презентация - Методическая разработка по теме Способы решения алгебраических уравнений.
- 2. Слайд 2
- 3. Уравнение
- 4. История развития знаний о решении
- 5. .22 решения за одну ночь.В 1594
- 6. Франсуа
- 7. Слайд 7
- 8. Сильвестр Джеймс Джозеф – английский математик, который ввел термин «дискриминант».
- 9. В
- 10. Виды алгебраических
- 11. Способы решения уравненийС помощью формул сокращенного умножения:(a±b)2=a2±2ab+b2a2-b2=(a+b)(a-b)(a1+a2+…+an)2=a12+a22+…+an2+2a1a2+2a1a3+…+2an-1an(a±b)3=a3±3a2b+3ab2±b3a3±b3=(a±b)(a2±ab+b2)an-1=(a-1)(an-1+an-2+…+an-k+…+a+1)an-bn=(a-b)(an-1+an-2b+…+an-kbk-n+…+abn-2+bn-1)ПРИМЕР
- 12. Способы решения уравнений(6x-1)2-4(3x+2)(3x-2)=-7;36x2-12x+1-4(9x2-4)=-7;36x2-12x+1-36x2+16=-7;17-12x=-7;-12x=-24;x=2;Ответ:{2}.(2x-1)3-(2x-3)3=24x2-40x-24;8x3-12x2+6x+1-8x3+36x2-54x-27=24x2-40x-24;24x2-48x-26=24x2-40x-24;-8x=2;x=-0,25;Ответ:{0,25}.
- 13. Способы решения уравнений Например:2х4 + 3х3 +
- 14. Метод группировки: Например:x4-4x3+5x2-4x+4=0;x4-4x3+4x2+x2-4x+4=0;(x4-4x3+4x2)+(x2-4x+4)=0;x2(x2-4x+4)+(x2-4x+4)=0;(x2+1)(x2-4x+4)=0;x2+1=0,x2-4x+4=0;x2=-1,(x-2)2=0;Ø,x-2=0;x=2;Ответ:{2}.Способы решения уравнений
- 15. Разложение левой части уравнения на множители.Решим уравнение
- 16. Метод выделения полного квадрата Решим уравнение х2
- 17. Решение квадратных уравнений по формуле Вывод формулы:Умножим
- 18. Например:4х2+ 7х + 3 = 0.а =
- 19. Теорема Виета Сумма корней приведенного
- 20. Теорема обратная теореме ВиетаЕсли числа m и
- 21. Свойства коэффициентов квадратного уравненияЕсли сумма
- 22. Решение уравнения несколькими способами. а) x2-6x+5=0x2-x-5x+5=0(x2-x)-(5x-5)=0x(x-1)-5(x-1)=0(x-5)(x-1)=0x-5=0,x-1=0;x=5,x=1.Ответ:{1; 5}.б) x2-6x+5=0x2-2·3·x+5=0x2-2·3·x+9-9+5=0(x-3)2-4=0(x-3)2=4x-3=2,x-3=-2;x=5,x=1.Ответ:{1; 5}.
- 23. в)x2-6x+5=0a=1b=-6c=5D=b2-4ac=36-4·1·5=36-20=16D>0, следовательноx=x=
- 24. По теореме обратной теореме Виетаг)x2-6x+5=0x1+x2=6x1x2=55=1·5 или 5=-1·(-5)x=1x=5Ответ: {1;5}
- 25. По свойству коэффициентов квадратного уравненияд) x2-6x+5=0a=1 , b=-6 , c=51-6+5=0 , значитx=1x=5Ответ: {1;5}
- 26. Слайд 26
- 27. Список использованной литературы .Алгебра. Сборник
Слайд 3 Уравнение – это золотой ключ, открывающий все математические
Историческая справка
Виды алгебраических уравнений
Способы решения уравнений
С помощью формул сокращенного умножения
Вынесение общего множителя за скобки
Метод группировки
Разложение левой части уравнения на множители.
Метод выделения полного квадрата.
Решение квадратных уравнений по свойству коэффициентов
Решение с помощью теоремы Виета.
Решение с помощью теоремы, обратной теореме Виета.
Решение уравнения несколькими способами.
Слайд 4 История развития знаний о решении уравнений.
Первое
Древние ученые владели общими приемами решения задач с неизвестными величинами. Но ни в одном источнике не дано описания этих приемов. Исключение- «Арифметика» Диофанта Александрийского. Первое руководство по решению задач - труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми.
Слайд 5 .
22 решения за одну ночь.
В 1594 году во дворе Генриха
Слайд 6 Франсуа Виет
Франсуа Виет -
Слайд 7 Кристиан Вольф - знаменитый немецкий философ, родился в 1679 г. в
Слайд 9 В 13 – 16 веках даются отдельные методы решения различных
Слайд 10 Виды алгебраических уравнений
Линейное уравнение
Квадратное уравнение ax2 + bx + c = 0
Кубическое уравнение ax3 + bx2 + cx + d = 0
Биквадратное уравнение ax4 + bx2 + c = 0
Уравнение 4-ой степени общего вида
ax4 + bx3 + cx2 + dx + e = 0
Алгебраическое уравнение n-ой степени общего вида
anxn + an-1xn-1 + ... + a1x + a0 = 0
Слайд 11Способы решения уравнений
С помощью формул сокращенного умножения:
(a±b)2=a2±2ab+b2
a2-b2=(a+b)(a-b)
(a1+a2+…+an)2=a12+a22+…+an2+2a1a2+2a1a3+…+2an-1an
(a±b)3=a3±3a2b+3ab2±b3
a3±b3=(a±b)(a2±ab+b2)
an-1=(a-1)(an-1+an-2+…+an-k+…+a+1)
an-bn=(a-b)(an-1+an-2b+…+an-kbk-n+…+abn-2+bn-1)
ПРИМЕР
Слайд 12Способы решения уравнений
(6x-1)2-4(3x+2)(3x-2)=-7;
36x2-12x+1-4(9x2-4)=-7;
36x2-12x+1-36x2+16=-7;
17-12x=-7;
-12x=-24;
x=2;
Ответ:{2}.
(2x-1)3-(2x-3)3=24x2-40x-24;
8x3-12x2+6x+1-8x3+36x2-54x-27=24x2-40x-24;
24x2-48x-26=24x2-40x-24;
-8x=2;
x=-0,25;
Ответ:{0,25}.
Слайд 13Способы решения уравнений
Например:
2х4 + 3х3 + х2 = 0;
x2(2x2+3x+1)=0;
x2=0,
2x2+3x+1=0;
x=0,
2x(x+1)+(x+1)=0;
x=0,
(2x+1)(x+1)=0;
x=0,
2x+1=0,
x+1=0;
x=0,
x=-0,5,
x=-1;
Ответ:
2. Вынесение общего множителя за скобки:
Слайд 14Метод группировки:
Например:
x4-4x3+5x2-4x+4=0;
x4-4x3+4x2+x2-4x+4=0;
(x4-4x3+4x2)+(x2-4x+4)=0;
x2(x2-4x+4)+(x2-4x+4)=0;
(x2+1)(x2-4x+4)=0;
x2+1=0,
x2-4x+4=0;
x2=-1,
(x-2)2=0;
Ø,
x-2=0;
x=2;
Ответ:{2}.
Способы решения уравнений
Слайд 15Разложение левой части уравнения на множители.
Решим уравнение х2 + 10х –
Разложим левую часть уравнения на множители:
х2 + 10х – 24 = х2 + 12х – 2х – 24 = х (х + 12) – 2 (х +12) = (х + 12)(х – 2)
Следовательно, уравнение можно переписать так:
(х + 12)(х – 2) = 0.
Так как произведение равно нулю, то по крайне мере один из его множителей равен нулю. Поэтому левая часть уравнения обращается в нуль при х = 2, а также при х = - 12. это означает, что числа 2 и – 12 являются корнями уравнения х2 + 10х – 24 = 0.
Слайд 16Метод выделения полного квадрата
Решим уравнение х2 + 6х – 7
х2 + 6х = х2 + 2· х ·3
х2 + 2· х ·3 + 32 = (х + 3)2
Преобразуем теперь левую часть уравнения
х2 + 6х – 7 = 0,
прибавляя к ней и вычитая 32.
х2 + 6х – 7 = х2 + 2· х ·3 + 32 – 32 – 7 =
= (х + 3)2 – 9 – 7 = (х + 3)2 – 16
Данное уравнение можно записать так:
(х + 3)2 –16 = 0,
т.е. (х + 3)2 = 16.
Следовательно, х + 3 = 4, х = 1, или х +3 = - 4 , х = – 7.
Слайд 17Решение квадратных уравнений по формуле
Вывод формулы:
Умножим обе части уравнения
ах2 +
на 4а и следовательно имеем:
4а2х2 + 4аbс + 4ас = 0.
((2ах)2 + 2ах · b + b2) – b2 + 4ас = 0,
(2ах + b)2 = b2 – 4ас,
2ах + b = ±
2ах = – b ±
Х =
Слайд 18Например:
4х2+ 7х + 3 = 0.
а = 4, b = 7,
D = b2 – 4ас = 72 – 4· 4 ·3 = 49 – 48 = 1,
D >0
х = ,
х = ;
х = ,
х = ,
х = ,
х = –1
Таким образом, в случае положительного дискриминанта,
т. е. при b2 – 4ас>0 уравнение ах2 + bх + с = 0 имеет два различных корня.
Слайд 19
Теорема Виета
Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому
Слайд 20Теорема обратная теореме Виета
Если числа m и n таковы, что их
ax2+bx+c=0
Слайд 21 Свойства коэффициентов квадратного уравнения
Если сумма коэффициентов квадратного уравнения ax2+bx+c=0
Если а- в+ с= 0 или в=а+с, то x= -1, х= c\а
Слайд 22Решение уравнения несколькими способами.
а) x2-6x+5=0
x2-x-5x+5=0
(x2-x)-(5x-5)=0
x(x-1)-5(x-1)=0
(x-5)(x-1)=0
x-5=0,
x-1=0;
x=5,
x=1.
Ответ:{1; 5}.
б) x2-6x+5=0
x2-2·3·x+5=0
x2-2·3·x+9-9+5=0
(x-3)2-4=0
(x-3)2=4
x-3=2,
x-3=-2;
x=5,
x=1.
Ответ:{1; 5}.
Слайд 23
в)x2-6x+5=0
a=1
b=-6
c=5
D=b2-4ac=36-4·1·5=36-20=16
D>0, следовательно
x=
x=
x= ; ; x=1
Ответ:{1; 5}.
Слайд 24По теореме обратной теореме Виета
г)x2-6x+5=0
x1+x2=6
x1x2=5
5=1·5 или 5=-1·(-5)
x=1
x=5
Ответ: {1;5}
Слайд 25По свойству коэффициентов квадратного уравнения
д) x2-6x+5=0
a=1 , b=-6 , c=5
1-6+5=0
x=1
x=5
Ответ: {1;5}
Слайд 26 Заключение
Математическое
Слайд 27Список использованной литературы
.
Алгебра. Сборник задач для учащихся 8-9
Учебник для учащихся 9 класса с углубленным изучением математики. под редакцией Н. Я. Виленкина.
Математика. 8-9 классы: сборник элективных курсов. Выпуск-2. Автор-составитель: М.Е. Козина., г. Волгоград: Учитель,2010г.
Внеклассная работа по математике. Альхова З.Н., Макеева А.В., г. Саратов: Лицей, 2011г
Математика. Учебное пособие под редакцией Муравья Л.Я., г. Москва Бридж 2004г