- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Метод координат в пространстве
Содержание
- 1. Презентация Метод координат в пространстве
- 2. 1.Актуальность2. Тематическое планирование (фрагмент)3. Теоретические сведения
- 3. Актуальность проблемыРешение задач геометрического содержания традиционно вызывает
- 4. «Сокращение преподавания геометрии в большом числе
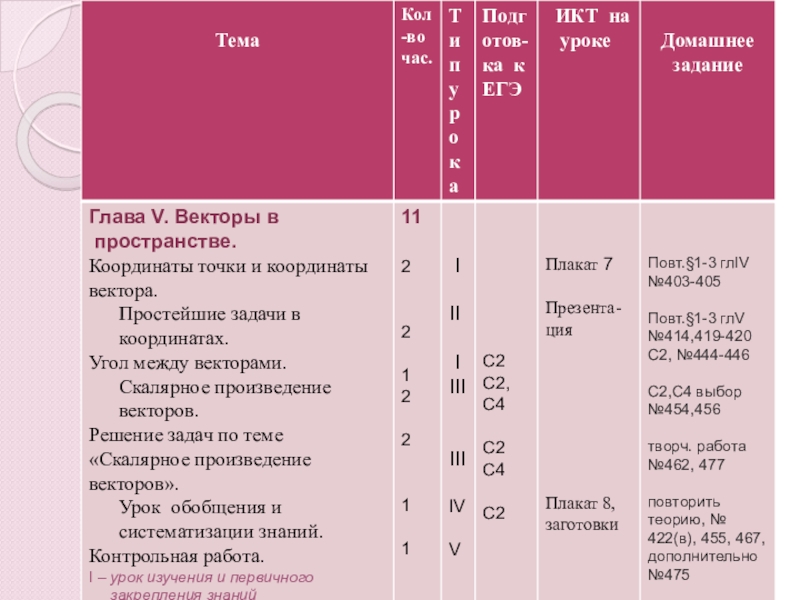
- 5. Примерное тематическое планирование учебного материала по геометрии в 11 классе
- 6. Повторить понятие прямоугольной системы координат в пространстве,
- 7. Координаты точки, координаты вектора. Связь между координатами
- 8. Формулы для решения задач:Координаты середины отрезка равны
- 9. Угол между векторами. Скалярное произведение векторов Угол
- 10. Ключевые задачи раздела№401 Найдите координаты проекций точек
- 11. Краткий план-коспект урока обобщения и систематизации знаний
- 12. Контрольная работаВариант1 1) Даны точки А(-1; 0,25;
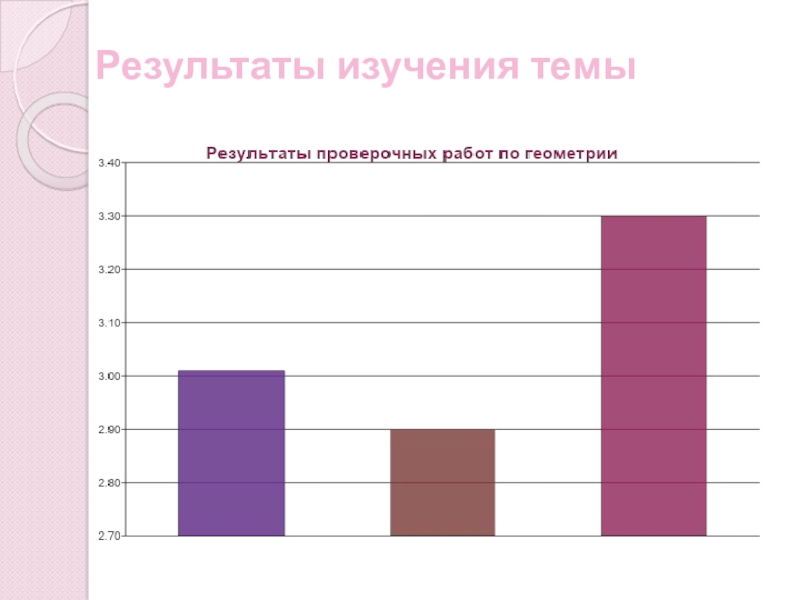
- 13. Результаты изучения темы
- 14. Соs a=Примеры решения задач ЕГЭС2(53) АВСDА1В1С1D1–правильная призма.
- 15. Примеры решения задач ЕГЭС2 Дан АВСDА1В1С1D1 –прямоугольный
- 16. Примеры решения задач ЕГЭС2 Дан АВСDА1В1С1D1 –прямоугольный
- 17. Примеры решения задач ЕГЭС2 В прямоугольном параллелепипеде
- 18. Примеры решения задач ЕГЭДана правильная треугольная призмаАВСА1В1С1,
- 19. Задачи для самостоятельного решенияС21 АВСDА1В1С1D1 - правильная
- 20. Для тех, кто хочет знать большеРассмотрим различные
- 21. Для тех, кто хочет знать большеРасстояние от
- 22. Для тех, кто хочет знать большеГеометрический способСделаем
- 23. Для тех, кто хочет знать большеВекторный способПусть
- 24. Для тех, кто хочет знать большеС2 (пример
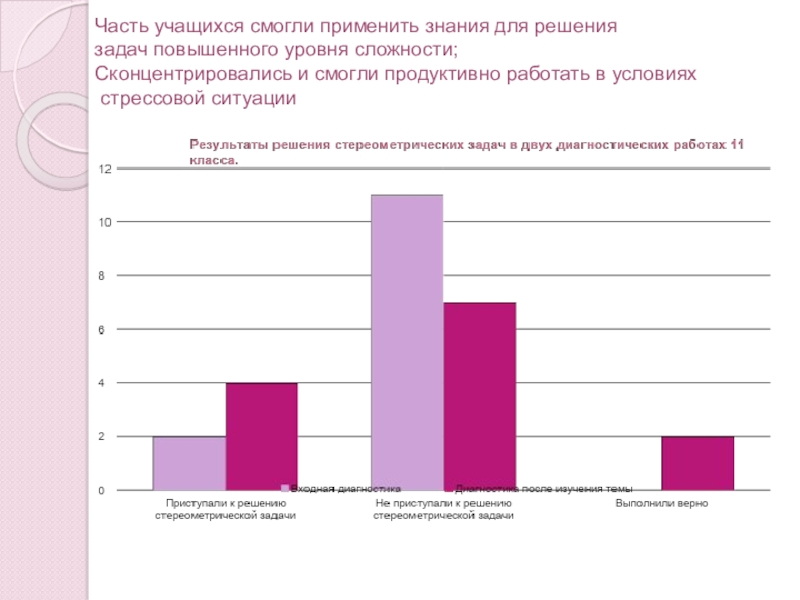
- 25. Часть учащихся смогли применить знания
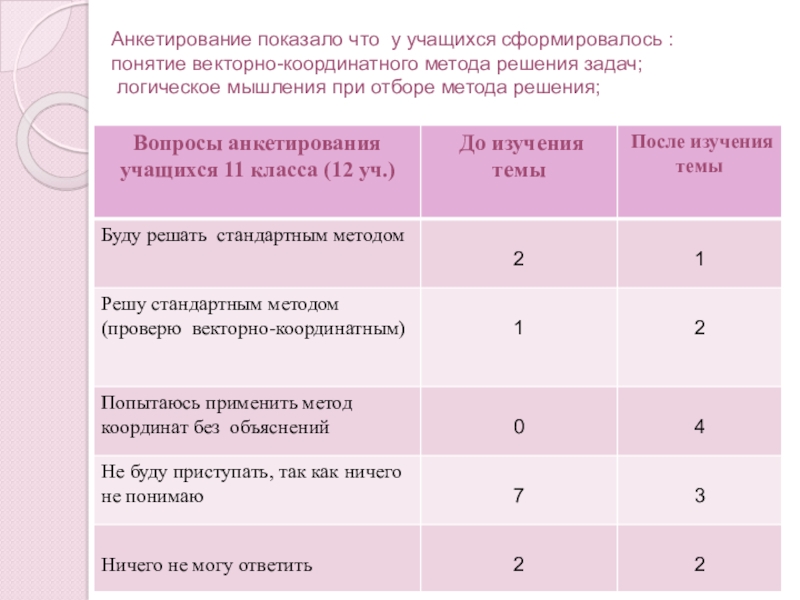
- 26. Анкетирование показало что у учащихся
- 27. Список используемой литературы:Геометрия. Учебник для общеобразовательных учреждений;Москва;
Слайд 1МОУ Алешковская средняя общеобразовательная школа
«Метод координат в пространстве».
Применение метода при решении
повышенного уровня сложности
Методическая разработка раздела образовательной программы
по геометрии Л.С. Атанасяна.
Выполнила:
учитель математики
1 квлификационной категории
Зуева Н.В.
2012 год
Слайд 2
1.Актуальность
2. Тематическое планирование (фрагмент)
3. Теоретические сведения ( глава 5, учебник )
5. План-конспект урока обобщения знаний
6. Пример проверочной работы по теме
«Метод координат в пространстве»
7. Решение аналогичных заданий ЕГЭ
векторно-координатным методом
8. Задачи для самостоятельного решения (с ответами)
9. Для тех, кто хочет знать больше
10. Заключение (диагностика)
11. Список используемой литературы.
Содержание работы:
Слайд 3Актуальность проблемы
Решение задач геометрического содержания традиционно вызывает у учащихся непреодолимые трудности.
Из справки 2010 года:
К заданию С2 приступили 3,7 % всех учащихся
(0,6 % учащихся района).
Одним из методов решения стереометрических
задач является координатно-векторный метод.
Он не требует знания большого количества
теорем, достаточно нагляден и позволяет
решить часть заданий С2 учащимся со средним
уровнем подготовки.
Слайд 4
«Сокращение преподавания геометрии в большом числе школ определяется, в том числе,
В геометрической подготовке выпускников имеются пробелы в развитии пространственных представлений, умении правильно изобразить геометрические фигуры, провести дополнительные построения, провести вычисления, применить полученные знания к решению практических задач.
При преподавании геометрии необходимо, прежде всего, уделять внимание формированию базовых знаний курса стереометрии (угол между прямыми в пространстве, угол между прямой и плоскостью, угол между плоскостями, многогранники и т.д.). Одновременно необходимо находить применение геометрических знаний к решению практических задач.»
Цитата из методического письма:
Слайд 6
Повторить понятие прямоугольной системы координат в пространстве, находить координаты точки в
Ввести понятие координат вектора в данной системе координат,
выработать умения и навыки выполнения действий над векторами
Вывести формула середины отрезка, длины вектора через его координаты и расстояния между двумя точками;
Ввести понятия угла между векторами и скалярного произведения векторов;
Сформировать у учащихся понятия векторно-координатного метода решения задач; применить этот метод для решения задач ЕГЭ ;
Развить логического мышления при отборе метода решения;
Сформировать у школьников исследовательские умения ;
Повышение культуры общения;
Выработать у школьников умение концентрироваться и продуктивно работать в условиях экзамена;
Применять знания для решения заданий повышенного уровня сложности.
Цели и задачи:
Основные цели и задачи изучении раздела:
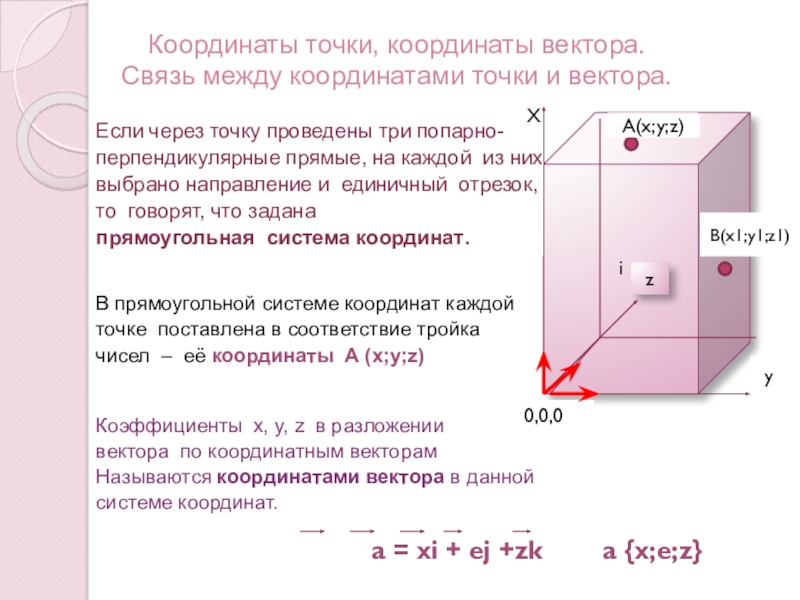
Слайд 7Координаты точки, координаты вектора.
Связь между координатами точки и вектора.
Если через точку
перпендикулярные прямые, на каждой из них
выбрано направление и единичный отрезок,
то говорят, что задана
прямоугольная система координат.
В прямоугольной системе координат каждой
точке поставлена в соответствие тройка
чисел – её координаты А (х;у;z)
Коэффициенты х, у, z в разложении
вектора по координатным векторам
Называются координатами вектора в данной
системе координат.
а = хi + ej +zk a {x;e;z}
i
Х
z
y
0,0,0
А(х;у;z)
В(х1;у1;z1)
Слайд 8Формулы для решения задач:
Координаты середины отрезка равны полусумме соответствующих координат его
ОС=0,5(ОА + ОВ) или
Х= 0,5(х1 +х2), У= 0,5(у1+у2),
Z =0,5(z1 +z2)
Вычисление длины вектора по его координатам
IаI = √х2+у2 +z2
Расстояние между точками
М1(х1;у1;z1) и М2(х2;у2;z2)
вычисляется по формуле:
d = √(х1-х2)2 + (у1 – у2)2 + (z1 – z2)2
Слайд 9Угол между векторами.
Скалярное произведение векторов
Угол между векторами а и в равен
Скалярным произведением двух векторов
называется произведение их длин на
косинус угла между ними.
а в = IаI IвI соs а или
соs а = а в / IаI IвI
(х1х2 + у1у2 + z1z2 )
√х12 +у12 + z12 √х22 + у22 + z22
Для вычисления углов между двумя прямыми,
а также между прямой и плоскостью во многих
случаях удобно использовать скалярное
произведение векторов.
cоs a =
Слайд 10Ключевые задачи раздела
№401 Найдите координаты проекций точек А(2; -3; 5), В(3;
№404 (устно) Даны векторы а(5;-1; 2), в(-3; -1; 0), с(0; -1; 0), d(0; 0; 0 ).
Определите разложение этих векторов по координатным векторам i, j, k .
№408 По данным рис. 132 найдите координаты векторов AС, СВ, АВ,
MN, NP, ВМ, ОМ, ОР, если ОА=4, ОВ=9, ОС=2, а M, N и Р – середины
отрезков АС, ОС и СВ.
№414 Найдите значения м и n, при которых следующие векторы
коллинеарны а) а(15; м; 1) и в(18; 12; n); б) с(m; 0,4; 1) и d(- ; n; 5).
№415 Компланарны ли векторы а) а(-3; -3; 0), i и j; б) в(2; 0; 3), i и j;
в) с(1; 0; -2), i и j; е) q(0; 5; 3), r(3; 3; 3) и s(1; 1; 4);
№430 Даны точки А( ; 1; -2 ), В(2; 2; -3) и С(2; 0; -1). Найдите
а) периметр треугольника АВС; б)медианы треугольника АВС.
№443 Ребро куба АВСDА1В1С1D1 равно а, точка О - центр грани А1В1С1D1.
Вычислите скалярное произведение векторов: АD и В1C1; АС и С1А1;
А1О1 и А1С1; D1О1 и В1О1; ВО1 и С1В.
№466 В кубе АВСDА1В1С1D1 точка М лежит на ребре АА1, причем АМ:МА1=3:1, а точка N –середина ребра ВС. Вычислите косинус угла между
прямыми а) МN и DD1; б) МN и В1D; в) MN и А1С; г) МN и ВD.
Слайд 11Краткий план-коспект урока обобщения и систематизации знаний
Тема урока: повторение и
«Координаты вектора. Скалярное произведение векторов».
Цели урока: повторяем формулы для нахождения длины вектора, скалярного
произведения векторов в координатах, косинуса угла между двумя прямыми
через координаты их направляющих векторов, решаем выборочно задачи из
учебника и аналогичные им задания С2 различными способами, сравниваем
способы решения, готовимся к контрольной работе.
Ход урока: на доске таблица, где изображен параллелепипед АВСDА1В1С1D1
с ребрами 1,2,3. Задание: введите систему координат с началом в
различных точках и определите длины векторов , углы между заданными
прямыми, углы между прямой и заданной плоскостью. Ответы сравниваем.
Аналогичная работа проводится для случая правильной призмы в основании
которой лежит квадрат (правильный треугольник). Решаем задачу №467 двумя
способами, сравнивая способы решения. Используем предыдущее домашнее
задание, приводим примеры задач из ЕГЭ и обговариваем ход решения.
В конце урока проводится самостоятельная работа на определение
коллинеарности двух векторов и компланарности трех векторов с самопроверкой
на доске.
Домашнее задание: повторить теорию, № 422(в), 455, 467, дополнительно №475
Слайд 12Контрольная работа
Вариант1
1) Даны точки А(-1; 0,25; 4,8)
В(3,9;-1,2; -5) и
Определите координаты
векторов АС, СВ, ВА и вид угла
между векторами АС и АВ
(острый, тупой, прямой).
2) Дан прямоугольный
параллелепипед со сторонами
5, 4 и 6 см. Найдите
расстояние от точки В до
середины DD1 и угол между
диагоналями соседних граней.
3) Определите лежат ли точки
А(5; -1; 0), В(-2; 7; 1), С(12;-15;-7)
И D(1; 1; -2) в одной плоскости.
Вариант 2
1)Даны точки А(-5; 2; 0) В(-4; 3;0)
С (-5; 2; -2). Определите вид
треугольника АВС.
2) Дан куб АВСDА1В1С1D1 со
стороной 2.
Найдите угол между
АМ и АN, где M – середина
стороны СВ, а N – середина
D1C1.
3) Определите компланарны
ли векторы АВ, АС и АВ,
если точки А,В,С,D имеют
координаты: А(-2; -3; 3),
В(1; 4; 1), С(-1; -1; -4) и
D(0; 0; 0) ?
Слайд 14Соs a=
Примеры решения задач ЕГЭ
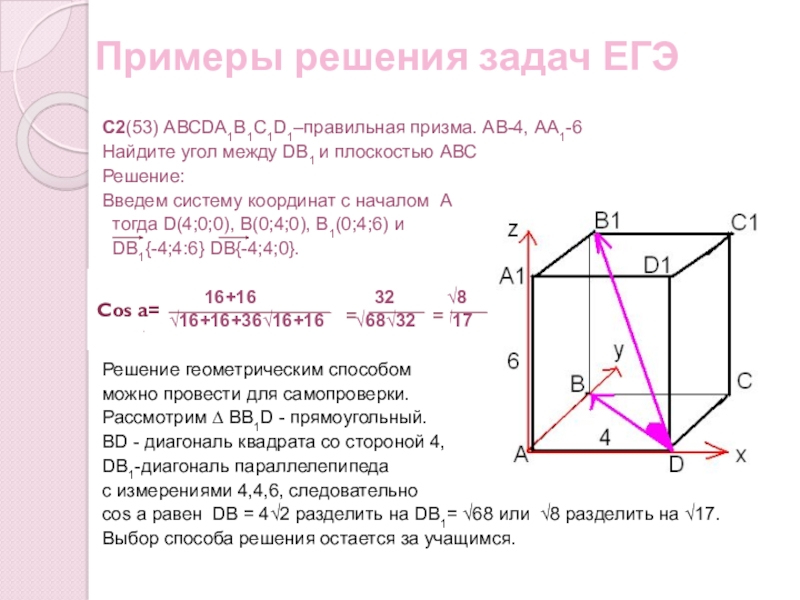
С2(53) АВСDА1В1С1D1–правильная призма. АВ-4, АА1-6
Найдите угол
Решение:
Введем систему координат с началом А
тогда D(4;0;0), В(0;4;0), В1(0;4;6) и
DВ1{-4;4:6} DВ{-4;4;0}.
16+16 32 √8
√16+16+36√16+16 √68√32 √17
Решение геометрическим способом
можно провести для самопроверки.
Рассмотрим ∆ ВВ1D - прямоугольный.
ВD - диагональ квадрата со стороной 4,
DВ1-диагональ параллелепипеда
с измерениями 4,4,6, следовательно
соs а равен DВ = 4√2 разделить на DВ1= √68 или √8 разделить на √17.
Выбор способа решения остается за учащимся.
=
=
Слайд 15Примеры решения задач ЕГЭ
С2 Дан АВСDА1В1С1D1 –прямоугольный параллелепипед АА1=3, АD=8, АВ=6,
Решение: геометрический способ
Слайд 16Примеры решения задач ЕГЭ
С2 Дан АВСDА1В1С1D1 –прямоугольный параллелепипед АА1=3, АD=8, АВ=6,
Решение: ( векторно-координатный способ )
Введем прямоугольную систему координат
С началом в точке А, тогда угол между
векторами АN {0;4;3} и АF1 {3;4;3} // ЕF и
будет искомым .
16+9 5
√25√34 √34
Косинус угла найден с помощью
формулы скалярного произведения двух
векторов.
Преимущество метода в этом случае
очевидно.
=
Соs a =
Слайд 17Примеры решения задач ЕГЭ
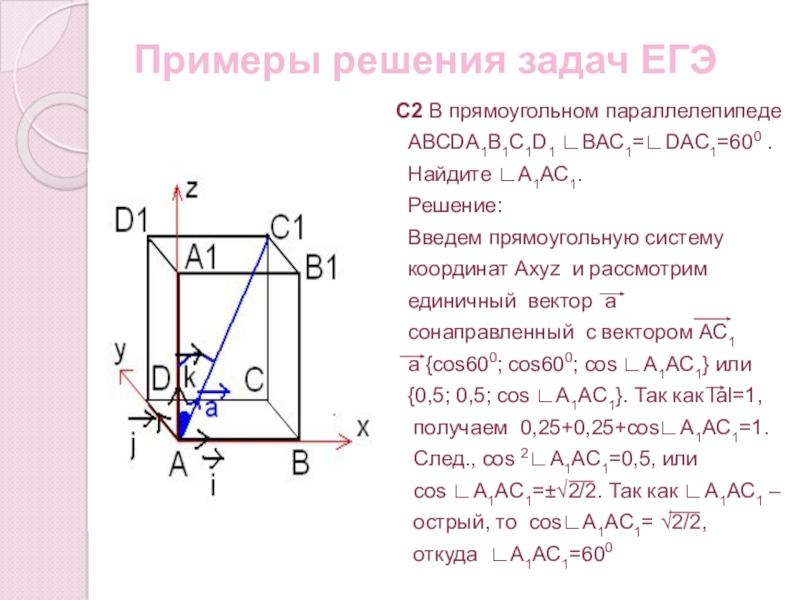
С2 В прямоугольном параллелепипеде
АВСDА1В1С1D1 ∟ВАС1=∟DАС1=600 .
Найдите
Решение:
Введем прямоугольную систему
координат Ахуz и рассмотрим
единичный вектор а
сонаправленный с вектором АС1
а {cos600; cos600; cos ∟A1AC1} или
{0,5; 0,5; cos ∟A1AC1}. Так как IaI=1,
получаем 0,25+0,25+cos∟A1AC1=1.
След., cos 2∟A1AC1=0,5, или
cos ∟A1AC1=±√2/2. Так как ∟A1AC1 –
острый, то соs∟A1AC1= √2/2,
откуда ∟А1АС1=600
Слайд 18Примеры решения задач ЕГЭ
Дана правильная треугольная призма
АВСА1В1С1, в которой АА1=√2АВ.
Найдите
Решение
Пусть АВ = х, тогда АА1=√2х.
Введем прям. с-му коор-т с началом в С.
А( ; ; 0), В(0; х; 0), А1( ; ; х√2),
С1(0; 0; х√2).
Выразим координаты векторов АС1 и ВА1
АС1{- ;- ;х√2),} BA1{ ;- ; х√2}
Угол между векторами и будет углом
между прямыми. Его соs равен
I-0,75Х2+0,25Х2+2Х2I
√-0,75Х2+0,25Х2+2Х2 √-0,75Х2+0,25Х2+2Х2
соs равен , откуда угол равен 600
Слайд 19Задачи для самостоятельного решения
С21 АВСDА1В1С1D1 - правильная призма. АВ=6, АА1 -
Найдите угол между В1D и плоскостью АВС (соs a = -2/ √13).
С22 АВСDА1В1С1D1 - правильная призма. АВ - 4, АА1 - 6.
Найдите угол между В1М и плоскостью АВС, где М –
середина АС (соs a = 1/ √11).
С23 Основанием прямой призмы АВСА1В1С1 является
равнобедренный треугольник АВС с основанием АВ,
причем АС - 4, С = 1200, боковое ребро АА1 равно 8.
Найдите угол между АС и ВВ1 (соs a = 0, ∟а =900).
С24 В правильной четырехугольной пирамиде сторона
основания равна 2 и равна высоте пирамиды. Найдите
угол наклона бокового ребра к плоскости основания
(соs a = 1/√3).
С25 В правильной треугольной призме АВСА1В1 С1, все
ребра которой равны 1. Найдите косинус угла между
прямыми АВ и СА1 (соs a = -1/ 2√2).
С26 В единичном кубе АВСDА1В1С1D1 найдите косинус угла
между плоскостями ABC и СВ1D1 (соs a = 1/√3).
Слайд 20Для тех, кто хочет знать больше
Рассмотрим различные методы решения одной из
нахождения расстояния между двумя скрещивающимися прямыми .
Чаще всего в задачах ЕГЭ предполагается использование формулы для
объема тетраэдра, образованного двумя скрещивающимися отрезками.
Но возможно применение и других способов.
Координатный способ
Пусть даны координаты точек, не лежащих в одной плоскости А(х1,у1,z1), В(х2,у2,z2), С(х3, у3,z3) и D(х4, у4, z4)
(тетраэдр с ребрами произвольной длины). Найти расстояние
между скрещивающимися прямыми АD и ВС.
Введем нормальный вектор плоскости n (а; в: с), который
перпендикулярен векторам АD и СВ. Нормалью к плоскости наз.
вектор, перпендикулярный к данной плоскости. В результате получаем
систему двух уравнений с тремя неизвестными:
n ∙ АD = 0, Уравнение плоскости, которой принадлежит т. А
n ∙ СВ = 0 или т.D имеет вид а(х-х1) + в(у-у1) + с(z-z1)=0
Слайд 21Для тех, кто хочет знать больше
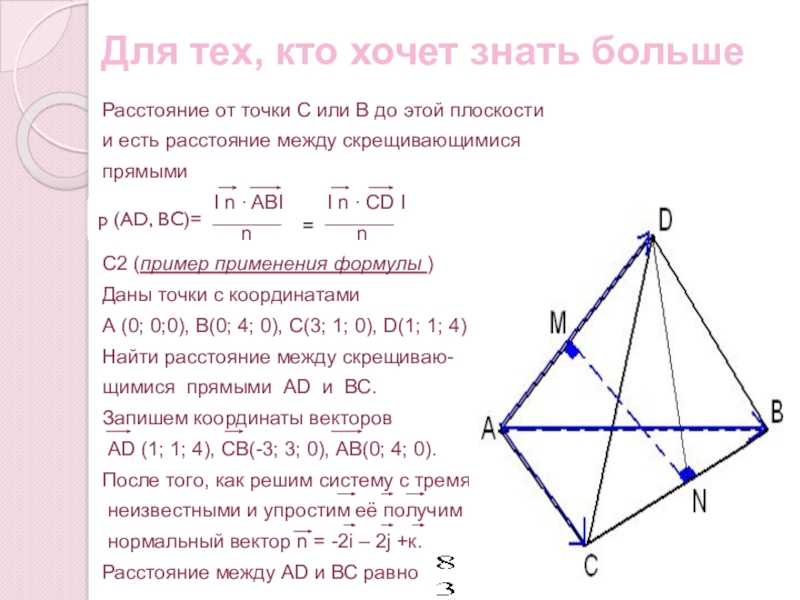
Расстояние от точки С или В
и есть расстояние между скрещивающимися
прямыми
I n ∙ ABI I n ∙ CD I
n n
С2 (пример применения формулы )
Даны точки с координатами
А (0; 0;0), В(0; 4; 0), С(3; 1; 0), D(1; 1; 4)
Найти расстояние между скрещиваю-
щимися прямыми АD и ВС.
Запишем координаты векторов
АD (1; 1; 4), СВ(-3; 3; 0), АВ(0; 4; 0).
После того, как решим систему с тремя
неизвестными и упростим её получим
нормальный вектор n = -2i – 2j +к.
Расстояние между АD и ВС равно
=
p (AD, BC)=
Слайд 22Для тех, кто хочет знать больше
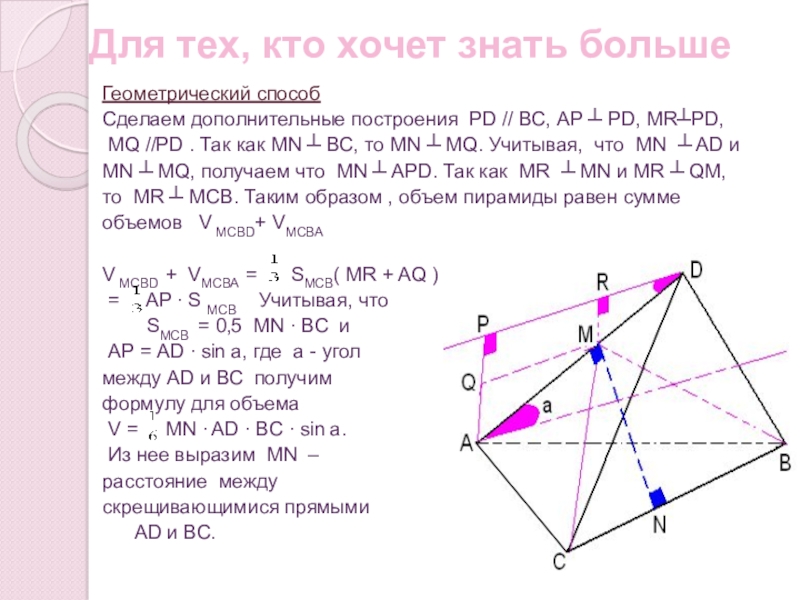
Геометрический способ
Сделаем дополнительные построения РD //
MQ //PD . Так как МN ┴ ВС, то МN ┴ МQ. Учитывая, что MN ┴ AD и
MN ┴ MQ, получаем что MN ┴ APD. Так как MR ┴ MN и MR ┴ QM,
то МR ┴ МСВ. Таким образом , объем пирамиды равен сумме
объемов V МСВD+ VМСВА
V МСВD + VМСВА = SМСВ( MR + AQ )
= AP ∙ S MCB Учитывая, что
SMCB = 0,5 MN ∙ BC и
АР = AD ∙ sin a, где а - угол
между AD и ВС получим
формулу для объема
V = MN ∙ AD ∙ BC ∙ sin a.
Из нее выразим MN –
расстояние между
скрещивающимися прямыми
AD и ВС.
Слайд 23Для тех, кто хочет знать больше
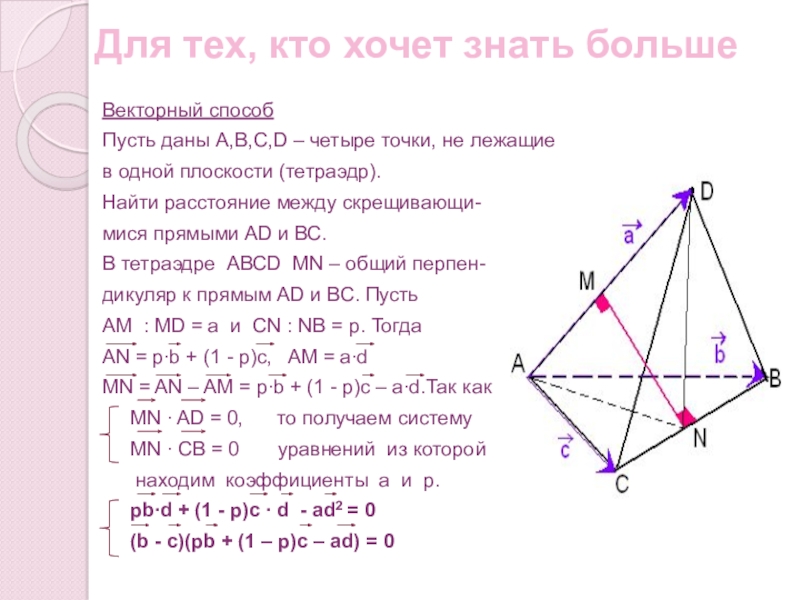
Векторный способ
Пусть даны А,В,С,D – четыре
в одной плоскости (тетраэдр).
Найти расстояние между скрещивающи-
мися прямыми АD и ВС.
В тетраэдре АВСD MN – общий перпен-
дикуляр к прямым АD и ВС. Пусть
AM : MD = а и СN : NВ = p. Тогда
AN = p∙b + (1 - p)c, AM = a∙d
MN = AN – AM = p∙b + (1 - p)c – a∙d.Так как
MN ∙ AD = 0, то получаем систему
MN ∙ CB = 0 уравнений из которой
находим коэффициенты а и p.
pb∙d + (1 - p)c ∙ d - ad2 = 0
(b - c)(pb + (1 – p)c – ad) = 0
Слайд 24Для тех, кто хочет знать больше
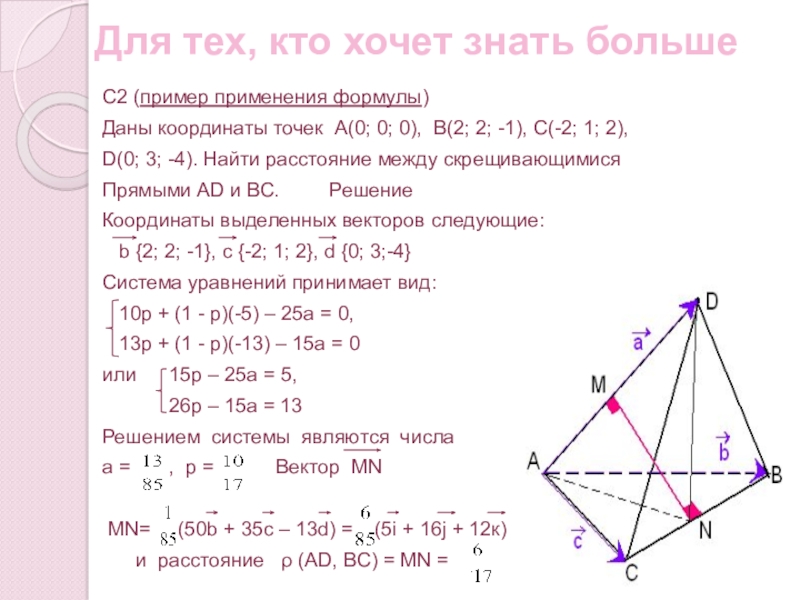
С2 (пример применения формулы)
Даны координаты точек
D(0; 3; -4). Найти расстояние между скрещивающимися
Прямыми АD и ВС. Решение
Координаты выделенных векторов следующие:
b {2; 2; -1}, с {-2; 1; 2}, d {0; 3;-4}
Система уравнений принимает вид:
10p + (1 - p)(-5) – 25а = 0,
13p + (1 - p)(-13) – 15а = 0
или 15p – 25а = 5,
26p – 15а = 13
Решением системы являются числа
а = , p = Вектор MN
MN= (50b + 35с – 13d) = (5i + 16j + 12к)
и расстояние ρ (AD, BC) = MN =
Слайд 25 Часть учащихся смогли применить знания для решения задач повышенного уровня сложности; Сконцентрировались
Слайд 26 Анкетирование показало что у учащихся сформировалось : понятие
Слайд 27Список используемой литературы:
Геометрия. Учебник для общеобразовательных учреждений;
Москва; «Просвещение», 2007год
Методические рекомендации к
«Векторы на экзаменах. Векторный метод в стереометрии», Шестаков С.А.; Москва, МЦНМО,2008 год
«Теоретические и практические вопросы подготовки к ЕГЭ по математике»; НИРО, 2009 год
ЕГЭ; «Интенсивная подготовка»; 2011 год,, тематические тренировочные задания
Сборник задач по математике. «Геометрия», под редакцией М.И. Сканави
Интернет-ресурсы:
http://www.ed.gov.ru Законы, указы, которые касаются вопросов
образования
http://www.niro.nnov.ru Нижегородский институт развития образования
http://www.it-n.ru Сеть творческих учителей
http://www.openclass.ru Открытый класс.
http://www.fipi.ru Материалы для подготовки к ЕГЭ.
http://www.mahtege.ru Открытый банк заданий по математике
http://www.rus.edu.ru Архив презентаций по всем предметам