- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к занятию Степенные ряды, область сходимости
Содержание
- 1. Презентация к занятию Степенные ряды, область сходимости
- 2. Определение Ряд, членами которого являются степенные
- 3. Областью определения степенного ряда является множество тех
- 4. Примеры: 1.Найти радиус и интервал сходимости степенного ряда
- 5. 2. Определить радиус и интервал сходимости степенного
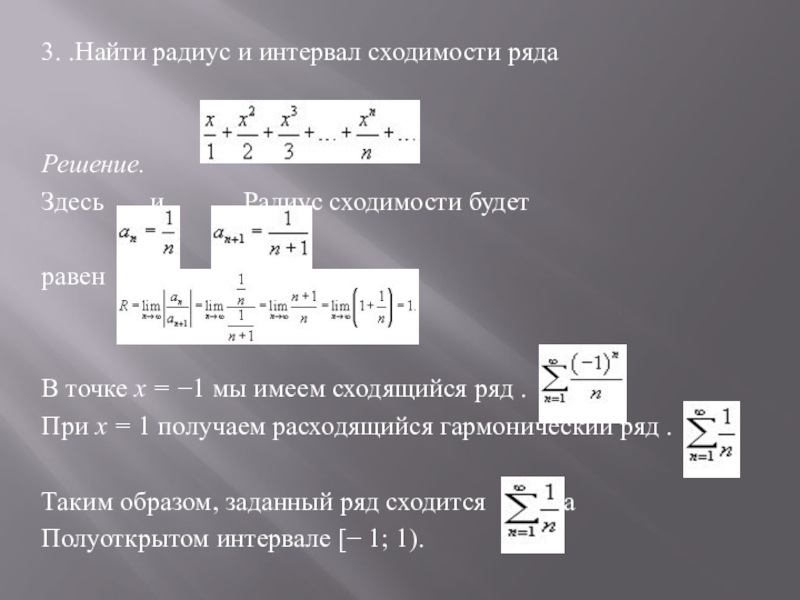
- 6. 3. .Найти радиус и интервал сходимости ряда
- 7. 3. При каких значениях x ряд сходится?
- 8. Найти радиус и интервал сходимости степенного ряда
- 9. Если u = −1, то такой ряд
- 10. 4. .Найти радиус и интервал сходимости степенного
- 11. Исследуем сходимости в конечных точках интервала. При
Определение Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом. Интервал и радиус сходимости Интервал сходимости степенного ряда - интервал действительных значений переменного, обладающий тем свойством, что в каждой точке этого интервала степенной ряд
Слайд 2Определение
Ряд, членами которого являются степенные функции аргумента x, называется степенным
рядом.
Интервал и радиус сходимости
Интервал сходимости степенного ряда - интервал действительных значений переменного, обладающий тем свойством, что в каждой точке этого интервала степенной ряд сходится, а в каждой точке, не принадлежащей к этому интервалу и не являющейся его концом,- расходится
Интервал и радиус сходимости
Интервал сходимости степенного ряда - интервал действительных значений переменного, обладающий тем свойством, что в каждой точке этого интервала степенной ряд сходится, а в каждой точке, не принадлежащей к этому интервалу и не являющейся его концом,- расходится
Слайд 3
Областью определения степенного ряда является множество тех значений x, при которых
ряд сходится. Область определения такой функции называется интервалом сходимости.
Если интервал сходимости представляется в виде , где R > 0, то величина R называется радиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно.
Радиус сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле
или на основе признака Даламбера:
Если интервал сходимости представляется в виде , где R > 0, то величина R называется радиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно.
Радиус сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле
или на основе признака Даламбера:
Слайд 4Примеры:
1.Найти радиус и интервал сходимости степенного ряда .
Решение.
Сделаем замену:
u = x + 3. Тогда ряд принимает вид .
Вычислим радиус сходимости:
Соответственно, интервал сходимости равен (− ∞; ∞).
Вычислим радиус сходимости:
Соответственно, интервал сходимости равен (− ∞; ∞).
Слайд 52. Определить радиус и интервал сходимости степенного ряда .
Решение.
Вычислим
радиус сходимости:
Рассмотрим сходимость в конечных точках.
Если x = −1, то мы имеем расходящийся ряд .
Если x = 1, то ряд также расходится.
Следовательно, исходный ряд сходится на открытом
интервале (− 1; 1).
Рассмотрим сходимость в конечных точках.
Если x = −1, то мы имеем расходящийся ряд .
Если x = 1, то ряд также расходится.
Следовательно, исходный ряд сходится на открытом
интервале (− 1; 1).
Слайд 63. .Найти радиус и интервал сходимости ряда
Решение.
Здесь и
. Радиус сходимости будет
равен
В точке x = −1 мы имеем сходящийся ряд .
При x = 1 получаем расходящийся гармонический ряд .
Таким образом, заданный ряд сходится на
Полуоткрытом интервале [− 1; 1).
равен
В точке x = −1 мы имеем сходящийся ряд .
При x = 1 получаем расходящийся гармонический ряд .
Таким образом, заданный ряд сходится на
Полуоткрытом интервале [− 1; 1).
Слайд 73. При каких значениях x ряд сходится?
Решение.
Найдем радиус и
интервал сходимости данного ряда.
Если x = −1, то получаем ряд
который сходится по признаку Лейбница.
Если же x = 1, то мы имеем расходящийся ряд:
Таким образом, интервал сходимости заданного ряда равен
[− 1; 1).
Если x = −1, то получаем ряд
который сходится по признаку Лейбница.
Если же x = 1, то мы имеем расходящийся ряд:
Таким образом, интервал сходимости заданного ряда равен
[− 1; 1).
Слайд 8Найти радиус и интервал сходимости степенного ряда .
Решение.
Сделаем замену:
u = x − 2. Тогда ряд запишется в виде .
Вычислим радиус сходимости:
Исследуем сходимость в конечных точках интервала.
Вычислим радиус сходимости:
Исследуем сходимость в конечных точках интервала.
Пример 5
Слайд 9Если u = −1, то такой ряд
будет сходиться как обобщенный
гармонический ряд с
показателем степени p =2 > 1.
Если u = 1, то получаем знакочередующийся ряд
который также сходится по признаку Лейбница.
Таким образом, интервал сходимости для ряда равен
[− 1; 1].
Поскольку новая и старая переменные связаны
соотношением u = x − 2, то интервал сходимости исходного
ряда будет равен
Ответ: исходный ряд сходится в интервале [1; 3].
показателем степени p =2 > 1.
Если u = 1, то получаем знакочередующийся ряд
который также сходится по признаку Лейбница.
Таким образом, интервал сходимости для ряда равен
[− 1; 1].
Поскольку новая и старая переменные связаны
соотношением u = x − 2, то интервал сходимости исходного
ряда будет равен
Ответ: исходный ряд сходится в интервале [1; 3].
Слайд 104. .Найти радиус и интервал сходимости степенного ряда
Решение.
Общий
член данного степенного ряда (начиная с n = 0),
выражается формулой
Здесь и .
Определим радиус сходимости:
выражается формулой
Здесь и .
Определим радиус сходимости:
Слайд 11Исследуем сходимости в конечных точках интервала.
При получаем
Этот ряд
сходится по признаку Лейбница.
При соответственно, имеем ряд
Применим для его анализа интегральный признак сходимости:
Следовательно, ряд расходится. Поэтому, интервал
Сходимости исходного ряда равен .
При соответственно, имеем ряд
Применим для его анализа интегральный признак сходимости:
Следовательно, ряд расходится. Поэтому, интервал
Сходимости исходного ряда равен .