запомню, сделай вместе со мной - и я научусь»
Китайская пословица
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к занятию Построение графика сложной функции путем преобразования элементарных
Содержание
- 1. Презентация к занятию Построение графика сложной функции путем преобразования элементарных
- 2. Тема: «Построение графика сложной функции путем преобразования элементарных функций».
- 3. Этап «Актуализация опорных знаний» Блиц-опрос.Фронтальный опрос.Игра
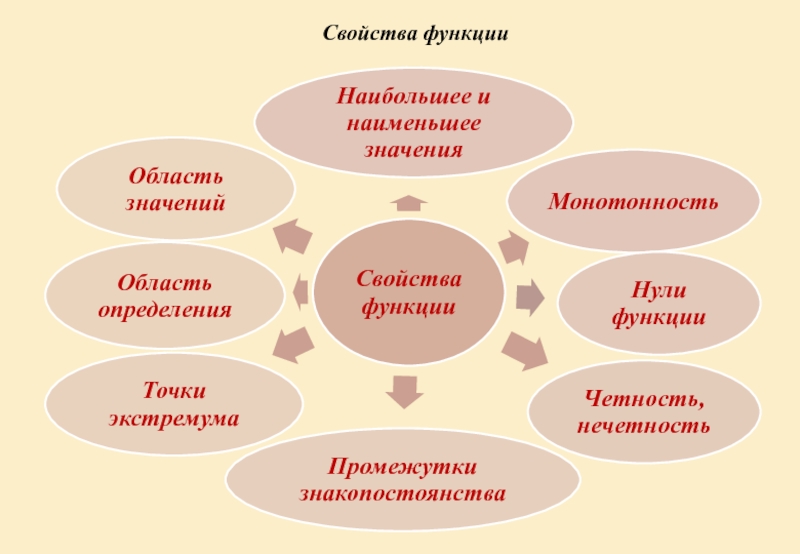
- 4. Свойства функцииМонотонностьНаибольшее и наименьшее значенияНули функцииЧетность, нечетность Промежутки знакопостоянстваТочки экстремумаОбласть определенияОбласть значенийСвойства функции
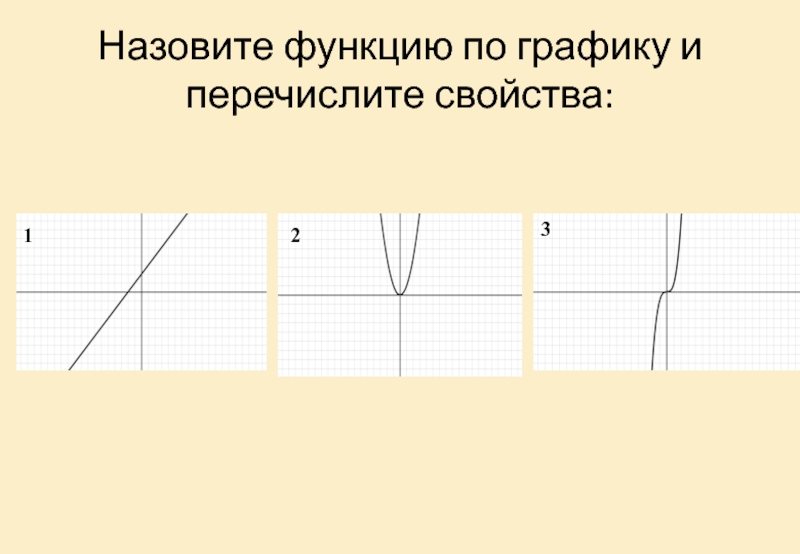
- 5. Назовите функцию по графику и перечислите свойства:123
- 6. Линейная функция y=kx+bСвойства линейной функции y =
- 7. Свойства функции y = kx2 при k
- 8. Свойства кубической функции y = x3:D(f) =
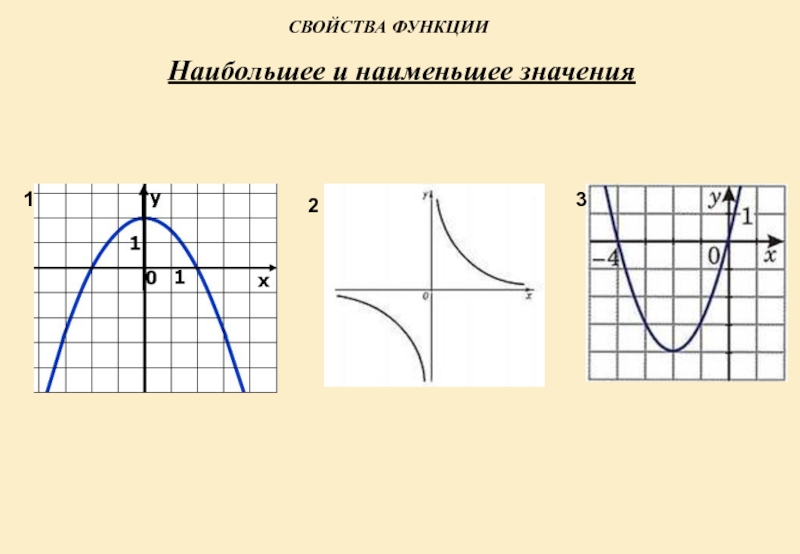
- 9. Наибольшее и наименьшее значенияСвойства функции123
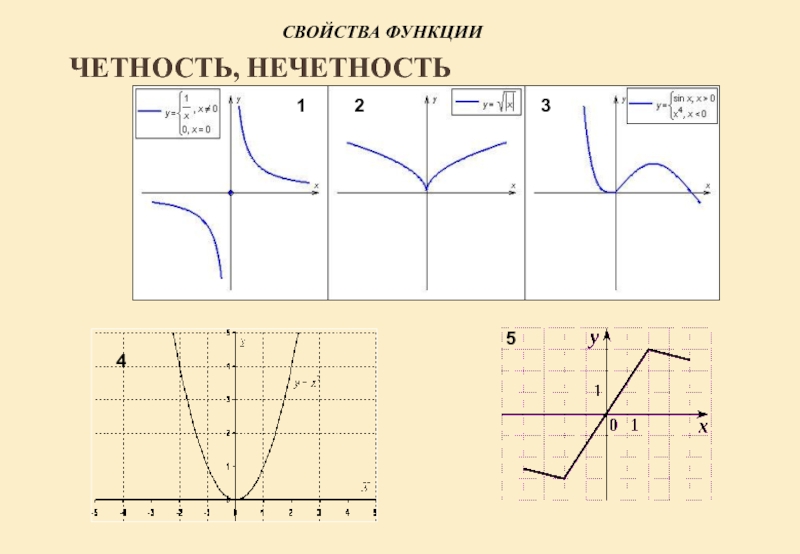
- 10. Свойства функцииЧЕТНОСТЬ, НЕЧЕТНОСТЬ45123
- 11. Свойства функцииD(f) = (-6, 4]Е(f) = [-1,
- 12. Математический диктант «Тригонометрические функции у =cos x;
- 13. Ответы: 1.2. Область определения:
- 14. Этап «Открытие новых знаний» ТЕМА: « Построение
- 15. Слайд 15
- 16. Слайд 16
- 17. Построим график функции y=cos хГрафиком является косинусоида, проходящая через точки: y=cos х
- 18. y=cos х
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. y=cos х
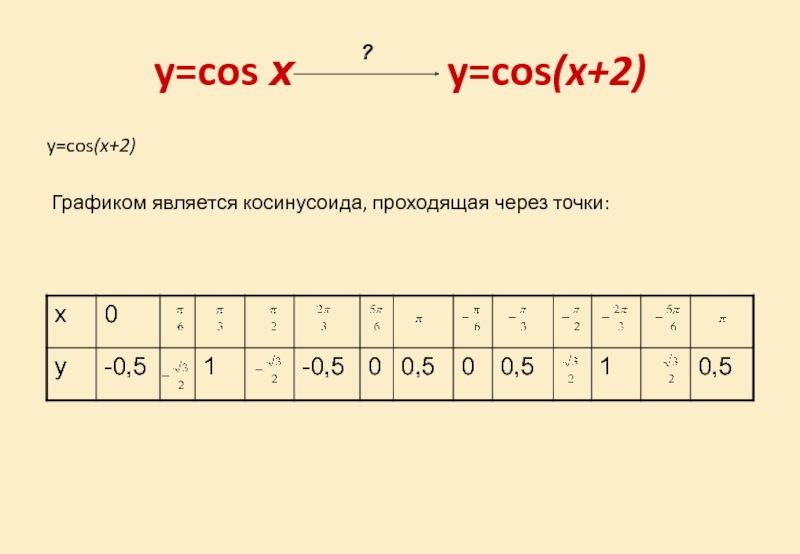
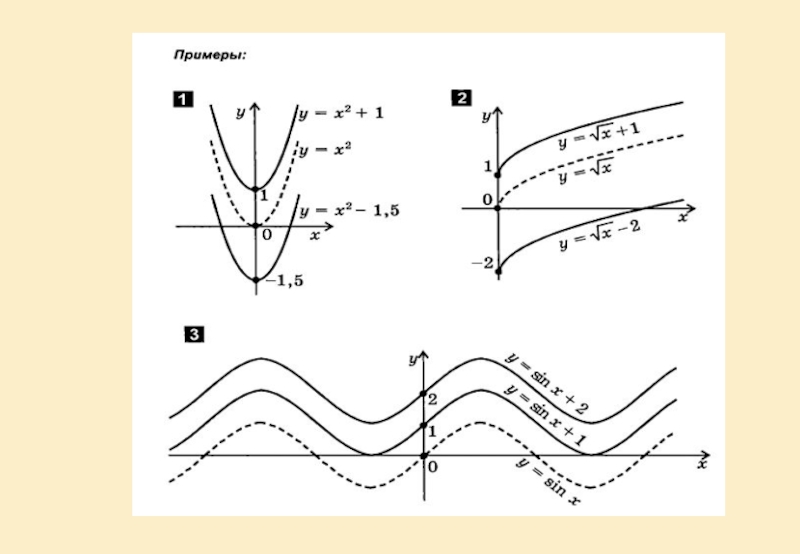
- 24. y=cos х y=cos(x+2)y=cos(x+2) Графиком является косинусоида, проходящая через точки:?
- 25. Слайд 25
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. y=cos х
- 30. y=cos х
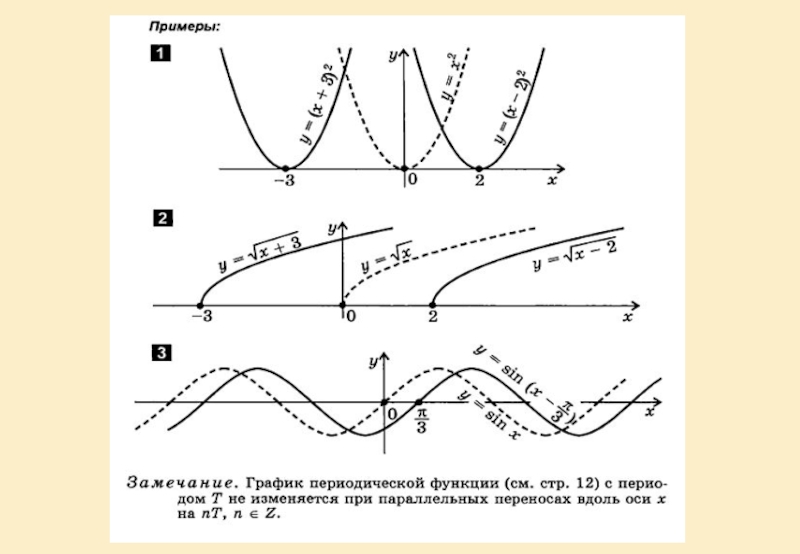
- 31. Построение графиков сложных функций с помощью последовательных преобразований элементарных функций (на примерах).
- 32. Слайд 32
Тема: «Построение графика сложной функции путем преобразования элементарных функций».
Слайд 3
Этап «Актуализация опорных знаний»
Блиц-опрос.
Фронтальный опрос.
Игра «Дальше, дальше…»
Работа по карточкам.
Математический диктант.
Сообщение по
теме: «Графики в нашей жизни».
Слайд 4Свойства функции
Монотонность
Наибольшее и наименьшее значения
Нули функции
Четность, нечетность
Промежутки знакопостоянства
Точки экстремума
Область определения
Область
значений
Свойства функции
Слайд 6Линейная функция y=kx+b
Свойства линейной функции y = kx + b:
D(f) =
(–; +).
E(f) = (–; +).
Если b = 0, то функция нечетная.
а) Нули функции: (– b/k; 0);
б) точка пересечения с Оу: (0; b).
а) возрастает, если k > 0;
б) убывает, если k < 0.
Не ограничена ни снизу, ни сверху.
Нет ни наибольшего, ни наименьшего значений.
Функция непрерывна на множестве (–; +).
E(f) = (–; +).
Если b = 0, то функция нечетная.
а) Нули функции: (– b/k; 0);
б) точка пересечения с Оу: (0; b).
а) возрастает, если k > 0;
б) убывает, если k < 0.
Не ограничена ни снизу, ни сверху.
Нет ни наибольшего, ни наименьшего значений.
Функция непрерывна на множестве (–; +).
Слайд 7Свойства функции y = kx2 при k > 0:
D(f) = (–;
+).
E(f) = [0; +).
Функция четная.
а) Нули функции: (0; 0);
б) точка пересечения с Оу: (0; 0).
а) [0; +) – промежуток возрастания функции;
б) (–; 0] – промежуток убывания функции.
Ограничена снизу, не ограничена сверху.
а) унаим. = 0;
б) унаиб. – не существует.
Непрерывна на множестве (–; +).
Выпукла вниз.
E(f) = [0; +).
Функция четная.
а) Нули функции: (0; 0);
б) точка пересечения с Оу: (0; 0).
а) [0; +) – промежуток возрастания функции;
б) (–; 0] – промежуток убывания функции.
Ограничена снизу, не ограничена сверху.
а) унаим. = 0;
б) унаиб. – не существует.
Непрерывна на множестве (–; +).
Выпукла вниз.
Квадратичная функция y=kx2
Слайд 8Свойства кубической функции y = x3:
D(f) = (–; +).
E(f) = (–;
+).
Функция нечетная.
а) Нули функции: (0; 0);
б) точка пересечения с Оу: (0; 0).
Возрастает на множестве (–; +).
Не ограничена ни снизу, ни сверху.
Нет ни наибольшего, ни наименьшего значений.
Функция непрерывна на множестве (–; +).
Функция нечетная.
а) Нули функции: (0; 0);
б) точка пересечения с Оу: (0; 0).
Возрастает на множестве (–; +).
Не ограничена ни снизу, ни сверху.
Нет ни наибольшего, ни наименьшего значений.
Функция непрерывна на множестве (–; +).
Кубическая функция y=x3
Слайд 11Свойства функции
D(f) = (-6, 4]
Е(f) = [-1, 5]
3. Ни четная, ни
нечетная
4. у= 0 при х= -2,8 х= -5
5. убывает на промежутках (-6;-4], [1;4]
возрастает на промежутке [-4;1]
6. Ограничена унаим.= -1, унаиб. = 5
7 . у>0 на промежутках (-6;-5), (-2,8;4]
y<0 на промежутке (-5; -2,8)
унаим.= -1, унаиб. = 5
8. Непрерывна
9. Выпуклость в точке xmax=1,
вогнутость в точке хmin= - 4
4. у= 0 при х= -2,8 х= -5
5. убывает на промежутках (-6;-4], [1;4]
возрастает на промежутке [-4;1]
6. Ограничена унаим.= -1, унаиб. = 5
7 . у>0 на промежутках (-6;-5), (-2,8;4]
y<0 на промежутке (-5; -2,8)
унаим.= -1, унаиб. = 5
8. Непрерывна
9. Выпуклость в точке xmax=1,
вогнутость в точке хmin= - 4
![Свойства функцииD(f) = (-6, 4]Е(f) = [-1, 5]3. Ни четная, ни нечетная4. у= 0 при х= -2,8](/img/thumbs/ef11b71639b7b05ddb3f1e7bb1908a63-800x.jpg "Презентация к занятию Построение графика сложной функции путем преобразования элементарных Свойства функцииD(f) = (-6, 4]Е(f) = [-1, 5]3. Ни четная, ни")
Слайд 12Математический диктант
«Тригонометрические функции у =cos x; y = sin x»
1 вариант
Построить
график
функции у = cos x.
2. Какова область определения косинуса?
3. Является ли функция у = cos x чётной или нечётной?
4. Каков наименьший положительный период функции у = cos x ?
5. Укажите нули функции у = cos x .
6. Укажите промежутки, на которых функция косинуса убывает (функция косинуса возрастает).
функции у = cos x.
2. Какова область определения косинуса?
3. Является ли функция у = cos x чётной или нечётной?
4. Каков наименьший положительный период функции у = cos x ?
5. Укажите нули функции у = cos x .
6. Укажите промежутки, на которых функция косинуса убывает (функция косинуса возрастает).
2 вариант
Построить график
функции у = sinx.
2. Какова область значения синуса?
3. Является ли функция y = sin x чётной или нечётной?
4. Каков наименьший положительный период функции y = sin x?
5. Укажите нули функции y = sin x.
Укажите промежутки, на которых функция синуса возрастает
( функция синуса убывает).
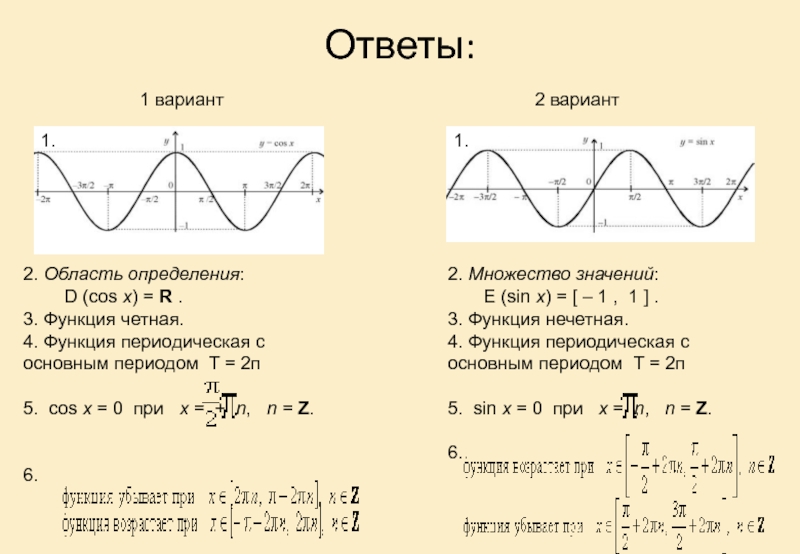
Слайд 13Ответы:
1.
2. Область определения:
D (cos x) = R .
3. Функция
четная.
4. Функция периодическая с основным периодом T = 2п
5. cos x = 0 при x = + n, n = Z.
6.
4. Функция периодическая с основным периодом T = 2п
5. cos x = 0 при x = + n, n = Z.
6.
1 вариант
2 вариант
1.
2. Множество значений:
E (sin x) = [ – 1 , 1 ] .
3. Функция нечетная.
4. Функция периодическая с основным периодом T = 2п
5. sin x = 0 при x = n, n = Z.
6.
Слайд 14Этап «Открытие новых знаний»
ТЕМА: « Построение графика сложной функции путем преобразования
элементарных функций».
Симметрия относительно осей координат.
Сдвиг вдоль осей координат (параллельный перенос).
Растяжение и сжатие графика вдоль осей координат.
Построение графика функции y=Af(k(x-a))+B по графику функции y=f(x).
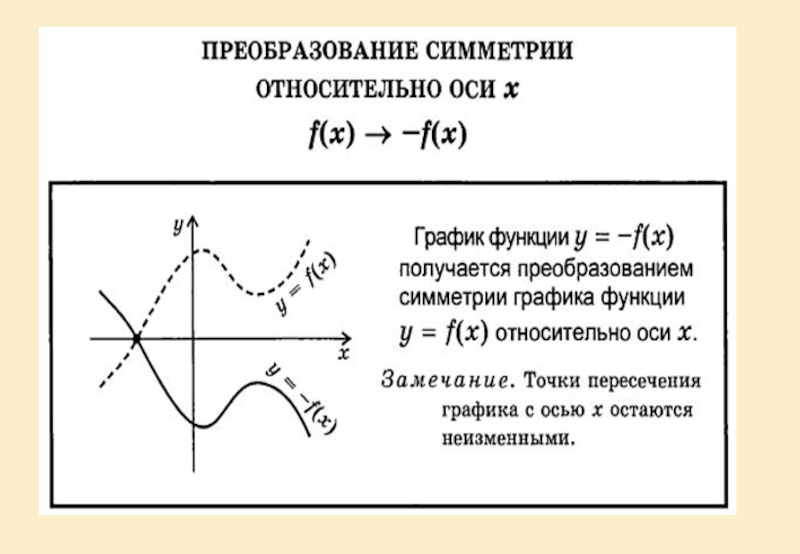
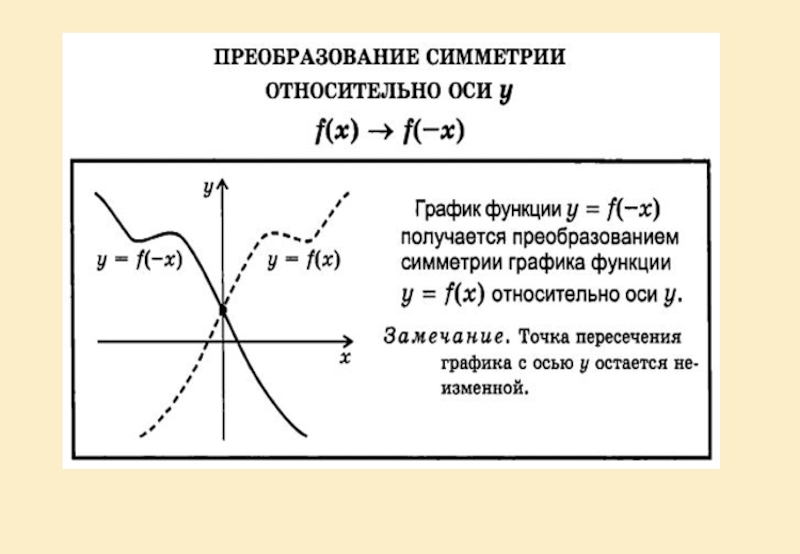
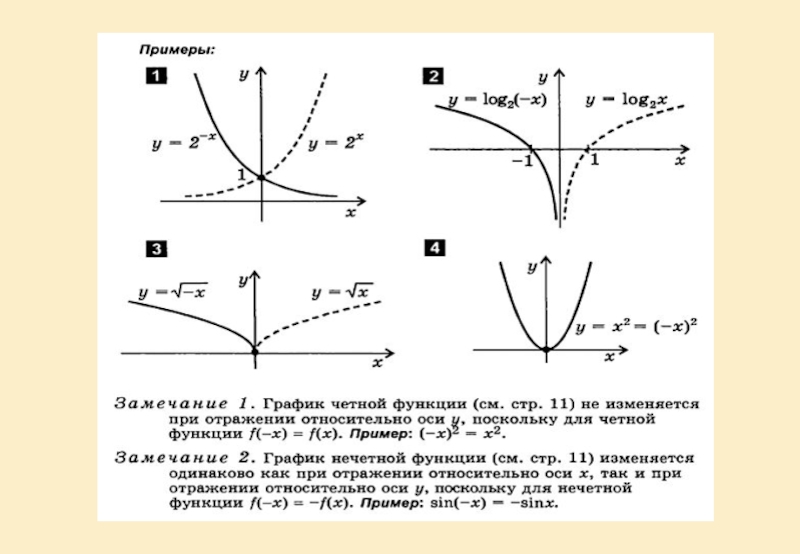
Симметрия относительно осей координат.
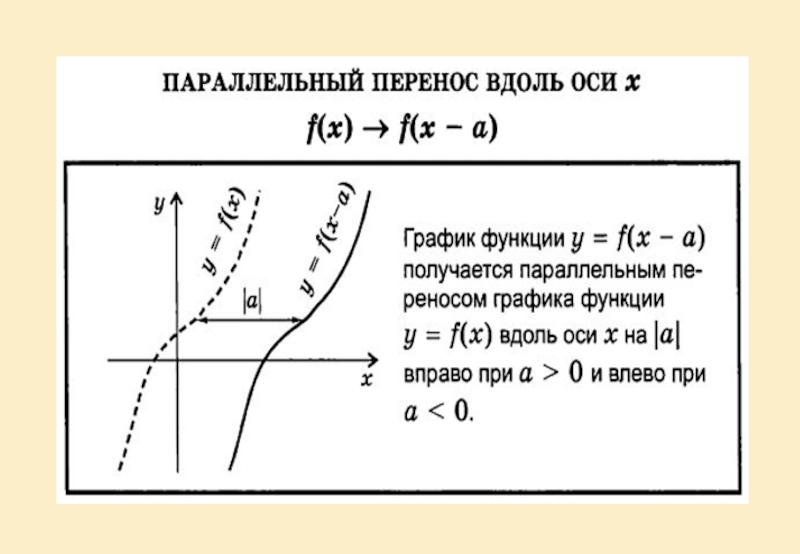
Сдвиг вдоль осей координат (параллельный перенос).
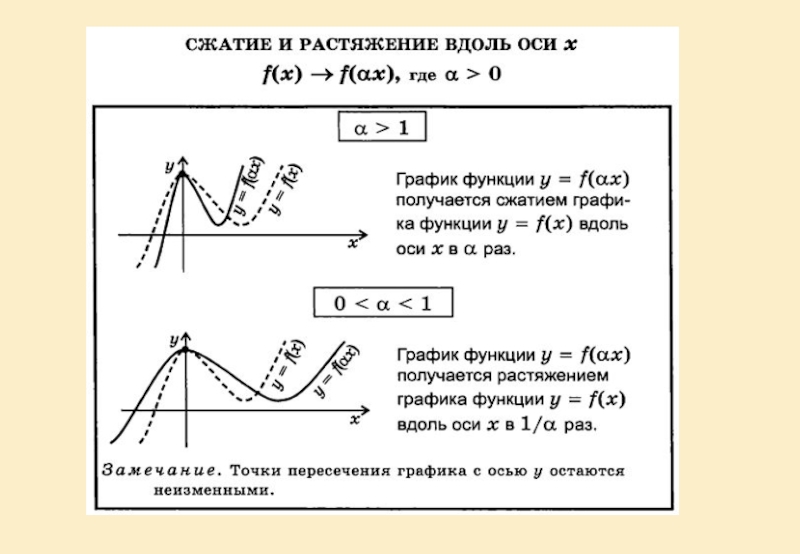
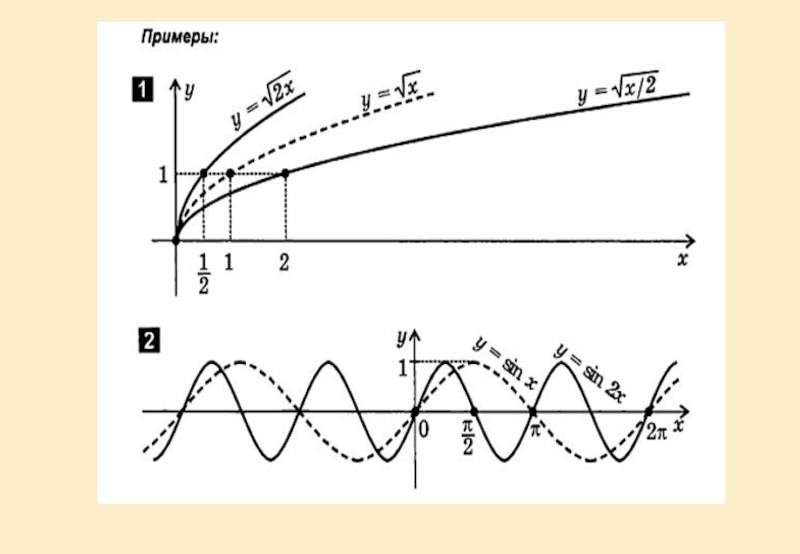
Растяжение и сжатие графика вдоль осей координат.
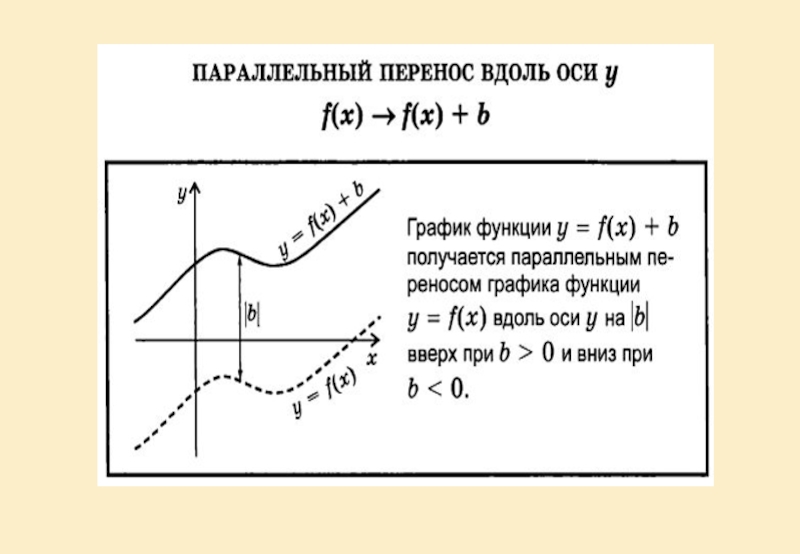
Построение графика функции y=Af(k(x-a))+B по графику функции y=f(x).
Слайд 17
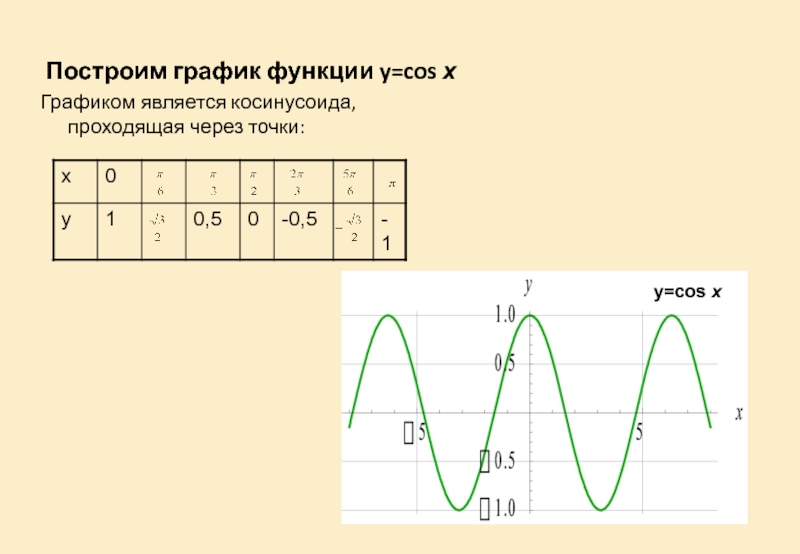
Построим график функции y=cos х
Графиком является косинусоида, проходящая через точки:
y=cos х
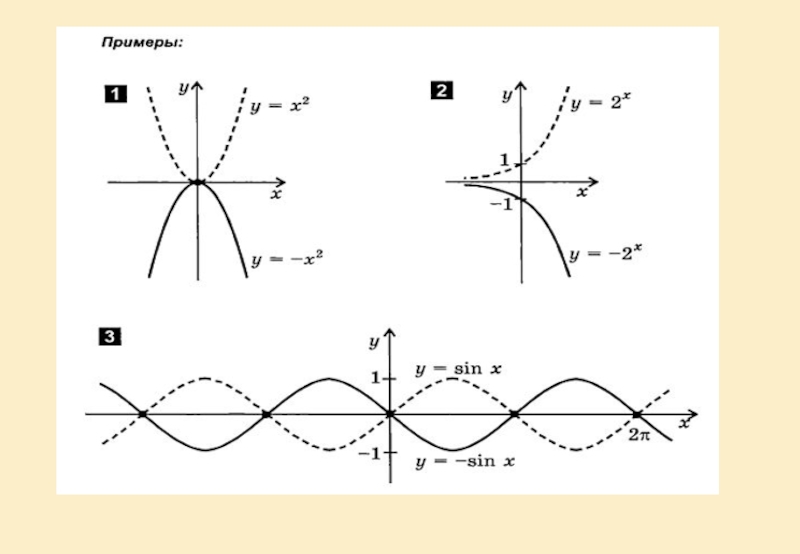
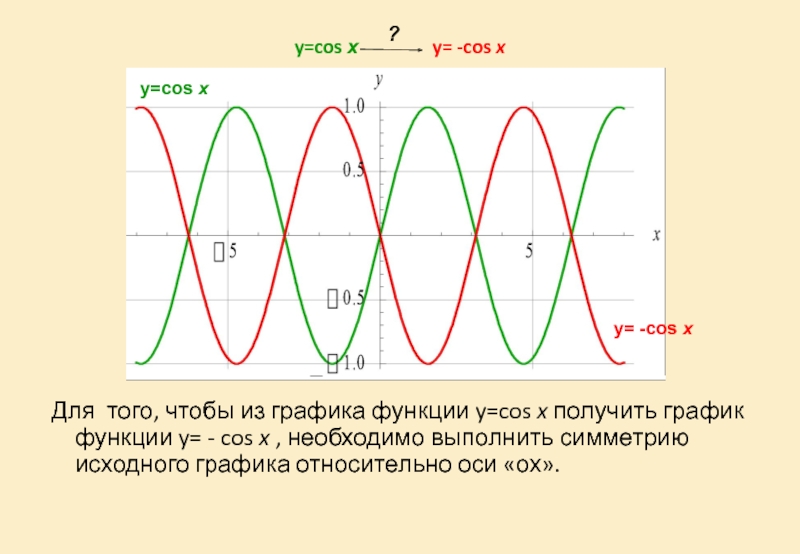
Слайд 18y=cos х y= -cos
x
Для того, чтобы из графика функции y=cos x получить график функции y= - cos x , необходимо выполнить симметрию исходного графика относительно оси «ох».
?
y=cos х
y= -cos x
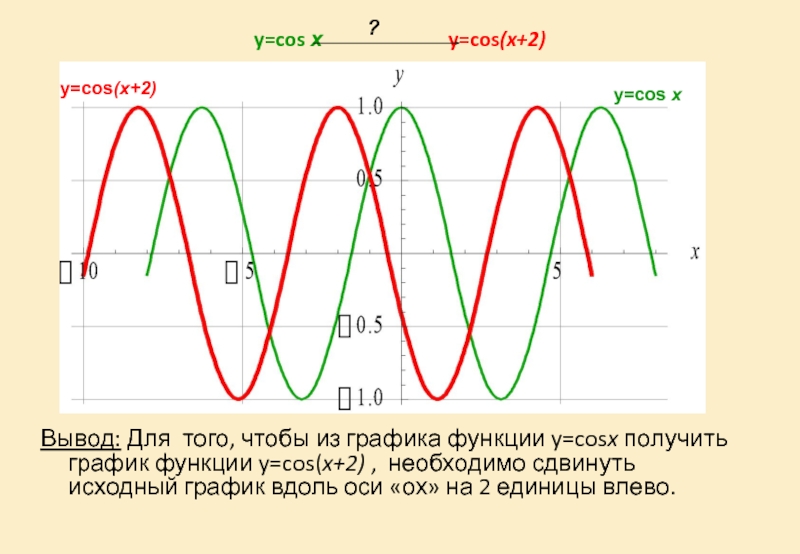
Слайд 23y=cos х y=cos(x+2)
Вывод: Для
того, чтобы из графика функции y=cosx получить график функции y=cos(x+2) , необходимо сдвинуть исходный график вдоль оси «ох» на 2 единицы влево.
?
y=cos х
y=cos(x+2)
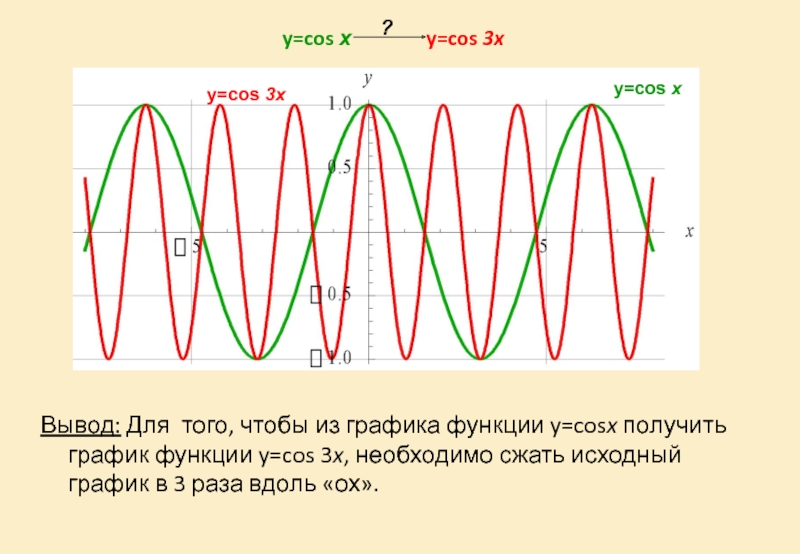
Слайд 29y=cos х y=cos 3x
Вывод:
Для того, чтобы из графика функции y=cosx получить график функции y=cos 3x, необходимо сжать исходный график в 3 раза вдоль «ох».
?
y=cos х
y=cos 3x
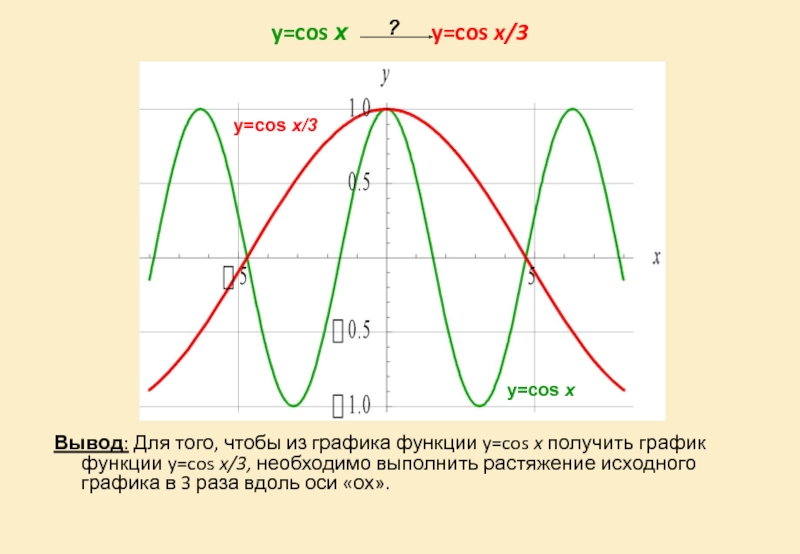
Слайд 30y=cos х y=cos x/3
Вывод:
Для того, чтобы из графика функции y=cos x получить график функции y=cos x/3, необходимо выполнить растяжение исходного графика в 3 раза вдоль оси «ох».
?
y=cos х
y=cos x/3
Слайд 31Построение графиков сложных функций с помощью последовательных преобразований элементарных функций (на
примерах).
