Учитель математики: Сингатулина М.И.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к выступлению на ШМО по теме: Устный счёт и его роль в изучение курса математики 5-6 классы
Содержание
- 1. Презентация к выступлению на ШМО по теме: Устный счёт и его роль в изучение курса математики 5-6 классы
- 2. «Хорошие навыки устных вычислений залог успешного изучения курса школьной математики».
- 3. В устных вычислениях нет готового шаблона, приемы
- 4. Три вида вычисления: письменное, устное и письменное с промежуточными устными вычислениями.
- 5. Виды упражнений по устному счету: 1.Слуховые
- 6. Задачи устного счета: •Воспроизводство и корректировка определённых
- 7. Требования к устному счету: •Упражнения для устного
- 8. Критерии оценки устного счета: •Задания на развитие
- 9. Найдите сумму чисел: а) 57 и
- 10. Для закрепления навыков использования понятия
- 11. Табличное умножение и деление натуральных чисел,
- 12. Найти значение выражения (упражнения по проверке
- 13. Сложение и вычитание десятичных дробей, имеющих одну-две
- 14. Решить задачу:
- 15. Умножение и деление десятичных дробей на 10,
- 16. Деление десятичной дроби на десятичную дробь:
- 17. Выразить проценты в виде десятичной дроби:
- 18. Решить задачу: а) Сережа на рыбалке
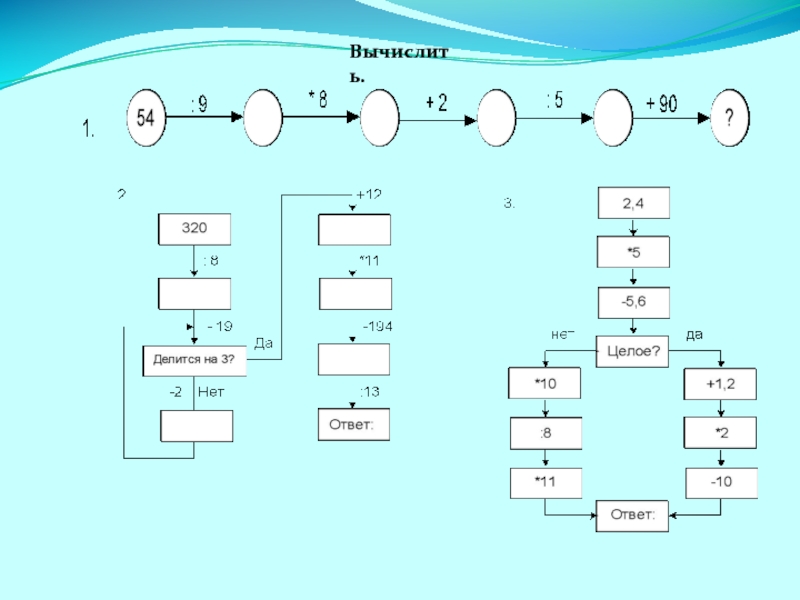
- 19. Вычислить.
- 20. Восстановить пропущенные цифры.
- 21. Найти ошибку.
- 22. Вычислить рационально. 144 –
- 23. Вместо квадратиков запишите такие числа, чтобы равенства оказались верными:
- 24. Слайд 24
- 25. 0,84 : 2,1 = 0,4- задание учителя
- 26. Лесенка
- 27. Молчанка.Эстафета. I команда
- 28. Не зевай. 6,2
- 29. Некоторые способы быстрых вычислений. Сложение и вычитание
- 30. 6) Сложение столбцами. Сумма
- 31. Способы быстрого умножения и деления натуральных чисел.1)
- 32. 3) Метод Ферроля. Для получения единиц
- 33. 4) Умножение чисел на 11 Записать
- 34. 7) Деление на 5, 25, 125
- 35. Представить каждое число ( от 1 до
- 36. 2. Магические квадраты (сумма чисел вдоль каждой
- 37. 3. Игры 1) Кто первый скажет
- 38. Роль устного счета в 5-6 класса является формирование у учащихся сознательных и прочных вычислительных навыков.
Слайд 1Тема: «Устный счёт и его роль в изучение курса математики 5-6
Слайд 3В устных вычислениях нет готового шаблона, приемы вычислений разнообразные, а поэтому
Слайд 5Виды упражнений по устному счету: 1.Слуховые упражнения :когда считающий воспринимает данные
Слайд 6Задачи устного счета: •Воспроизводство и корректировка определённых знаний, умений и навыков учащихся,
Слайд 7Требования к устному счету: •Упражнения для устного счета выбираются не случайно, а
Слайд 8Критерии оценки устного счета: •Задания на развитие и совершенствование внимания. Такие как:
Слайд 9 Найдите сумму чисел: а) 57 и 8
в) 37,29 и 13 ( (37+13)+29)
г) 86,35 и 15 ( 86+(35+15))
Увеличьте: а) 42 на 19 (42+20-1)
б) 170 на 80 (170+100-20)
Найдите разность чисел: а) 17 и 9 (17-10+1)
б) 120 и 31 (120-30-1)
Уменьшите: а) 28 на 9 в) 270 в 3 раза
б) 230 на 70 г) 250 в 5 раз.
Слайд 10Для закрепления навыков использования понятия «увеличить (уменьшить) на целое
а) На верхней полке 32 книги, что на 19 книг меньше (больше), чем на
нижней полке. Сколько книг на каждой полке?
б) Одно из чисел 111, что в 3 раза больше (меньше), чем другое. Найти эти
числа.
Слайд 11 Табличное умножение и деление натуральных чисел, но с различными
а) Найти произведение чисел: 8 и 7
9 и 4
б) Увеличьте: 6 в 5 раз
7 в 9 раз
в) Решите уравнение: х : 8 = 9
49 : х = 7
г) Найти задуманное число, если оно меньше 24 в 3 раза .
Слайд 12 Найти значение выражения (упражнения по проверке свойств и законов
а) 25·39 ·4 д) (25+7) ·4 - 4
б) 12 ·27 ·8 е) 486 – 16 · 0
в) 18 ·33 + 82 ·33 ж) 139·1 – 1·0
г) 59 ·47 - 49 ·47 з) 288 + 0 : 9
Слайд 13Сложение и вычитание десятичных дробей, имеющих одну-две значащие цифры, с одним
а) 0,6 + 0,9 г) 2,3 – 0,5
б) 0,4 + 1,8 д) 4,5 – 0,5
в) 9,2 + 0,8 е) 3,6 – 2,6
Сложение и вычитание целого числа и дроби:
а) 4 + 8,6 в) 1 – 0,3 д) 8,6 - 7
б) 6 – 1,8 г) 9 – 2,7 е) 1 – 0,5
Умножение и деление десятичных дробей на натуральное число:
а) 1,8 : 3 б) 6,9 : 3 в) 6,5 : 5 г) 7,5 : 3 д) 2 : 5
1,6 : 4 4,8 : 4 5,2 : 4 9,8 : 2 3 : 6
2,1 : 3 6,6 : 3 9,1 : 7 5,4 : 2 6 : 5
3,6 : 9 8,2 : 2 8,4 : 6 9,6 : 4 5 : 2
Слайд 14 Решить задачу:
б) Периметр квадрата равен 4,8м. Найти его сторону.
в) Какое число надо увеличить в 3 раза, чтобы получилось 4,5?
г) Во сколько раз 7,5 больше 3?
Решить уравнение:
а) 4х = 2,4 б) 3а = 9,3 в) 6y = 8,4 г) 2а = 5
7а = 1,4 4b = 8,4 3х = 7,8 2с = 9
8b = 4,8 2х = 6,6 2а = 7,4 8n = 4
Слайд 15Умножение и деление десятичных дробей на 10, 100, 1000,…
а) 1,03*10 б) 2,008*100 в) 2,9*1000
10*0,4 4,76*100 1,023*1000
6,8*10 3,185*100 2,9*1000 + 100
7,35*10 13,4*100 1,02*100 + 0,98
23,7 : 10 73,8 : 100 0,003*100 + 0,7
286,1 : 10 12 : 100 0,017*1000 – 1,1
5,49 : 10 3 : 100 0,15*100 + 0,005*1000
0,7 : 10 7,4 : 100 0,29*100 – 0,09*100
6 : 10 0,2 : 100 15,5 : 100 + 8,45 : 10
г) Увеличьте числа: 6,8; 7,35; 0,8; 0,503 в 10 раз
3,18; 15,4; 0,209; 0,3 в 100 раз
д) Уменьшите числа: 23,7; 286,1; 5,49; 0,7; 23; 6 в 10 раз
2; 19; 73,8; 0,7; 0,205 в 100 раз
Слайд 16Деление десятичной дроби на десятичную дробь:
а) Подготовить десятичную
2,5 : 0,5 3,6 : 0,03 7 : 0,7
48,48 : 0,04 10 : 2,5 1 : 0,125
б) Выполнить деление:
0,5 : 0,1 28,1 : 0,1
2 : 0,01 2,03 : 0,01
3,1 : 0,001 0,75 : 0,001
Сравнение десятичных дробей с обоснованием ответа:
0,3 и 0,9 ; 7,008 и 7,8;
5,035 и 15,065; 0,2857 и 2,857;
15,035 и 15,065; 28,573 и 28,389;
0,028 и 0,0028; 4,2781 и 4,2751;
Слайд 17Выразить проценты в виде десятичной дроби:
а) 1%, 9%, 30%.
б) 0,2%. 0,26%, 0,04%, 0,107%, 0,001%.
Выразить в процентах следующие числа:
а) 0,01; 0,09; 0,31; 0,032; 0,108; 0,0078.
б) 1,3; 1,03; 2; 21,7; 3,06; 8,005.
Найти 1% от 25, 250, 2500, 8, 80.
Найти 5% от 100, 500, 300, 20.
Какую часть числа составляют 1%, 5%, 20%, 25%, 50%, 100% ?
Слайд 18Решить задачу:
а) Сережа на рыбалке поймал 7 окуней, 4
б) В классе 40% всех учащихся составляют девочки. Сколько процентов всех учащихся составляют мальчики?
в) В магазине в первый день продали 25% всего товара, во второй день 35% товара. Сколько процентов товара осталось непроданным?
Слайд 22 Вычислить рационально.
144 – (14 + 38);
(212 + 134) – (112 + 34); 25 + 37 – 5; 1,1 * 15;
94427 + 1484) – 327; 5 * 8 * 4 * 125; 2,8 * 9;
Найти значения следующих сумм: 1 + 3 = (4);
1 + 3 + 5 = (9);
1 + 3 + 5 + 7 = (16);
1 + 3 + 5 + 7 + 9 = (25);
Слайд 250,84 : 2,1 = 0,4
- задание учителя
Равный счет.
Примерные ответы
0,2 · 2 = 0,4
40 : 100 = 0,4 и т.д.
Счет - дополнение
Учитель записывает на доске какое-то число, допустим, 1,5. Затем он медленно называет число, которое меньше, чем 1,5. Ученики в ответ должны назвать другое число, дополняющее данное до 1,5.
Учитель: Ученик:
1 0,5
0,3 1,2
0,7 0,8
1,4 0,1
1,1 0,4
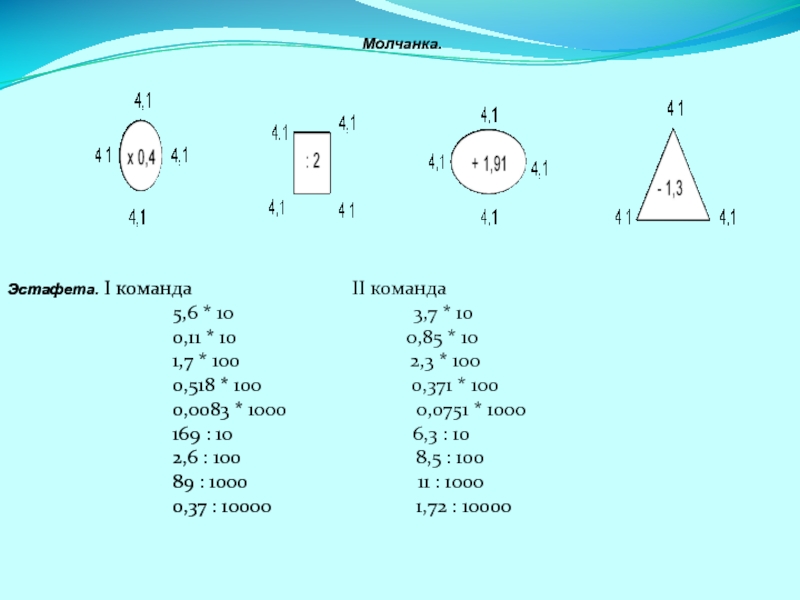
Слайд 27 Молчанка.
Эстафета. I команда
5,6 * 10 3,7 * 10
0,11 * 10 0,85 * 10
1,7 * 100 2,3 * 100
0,518 * 100 0,371 * 100
0,0083 * 1000 0,0751 * 1000
169 : 10 6,3 : 10
2,6 : 100 8,5 : 100
89 : 1000 11 : 1000
0,37 : 10000 1,72 : 10000
Слайд 28Не зевай.
6,2
… - 5,1 =
… + 3,09 =
… - 0,19 =
… * 2,2 =
Математический диктант. 5 класс.
слагаемое 28, II слагаемое 57. Найдите сумму этих чисел.
Уменьшаемое 64, вычитаемое 46. Найдите разность этих чисел.
Число 75 увеличьте на 17.
Найдите разность 51 и 38.
Найдите сумму 43 и 49.
Число 81 уменьшите на 24.
слагаемое 25, а второе на 14 больше. Найдите сумму этих чисел.
Слайд 29Некоторые способы быстрых вычислений.
Сложение и вычитание натуральных чисел.
1) Если
суммы надо вычесть столько же единиц.
364 + 592 = 364 + ( 592 + 8 ) – 8 = 364 + 600 – 8 = 956.
2) Если одно из слагаемых увеличить на несколько единиц, а другое
уменьшить на столько же единиц, то сумма не изменится.
997 + 856 = ( 997 + 3 ) + ( 856 – 3 ) = 1000 + 853 = 1853.
3) Если вычитаемое увеличить на несколько единиц и уменьшаемое
Увеличить настолько же единиц, то разность не изменится.
1351 – 994 = ( 1351 + 6 ) – ( 994 + 6 ) = 1357 – 1000 = 357.
4) Если от суммы двух чисел отнять разность этих же чисел, то в
результате получится удвоенное меньшее число.
( 57 + 23 ) – ( 57 – 23 ) = 46.
5) Если к сумме двух чисел прибавить их разность, то в результате
получится удвоенное большее число.
( 74 + 26 ) + ( 74 – 26 ) = 148.
Слайд 306) Сложение столбцами.
Сумма цифр каждого разряда складывается
в сумме предыдущего разряда складывается с цифрой единиц
последующей суммы.
Слайд 31Способы быстрого умножения и деления натуральных чисел.
1) Применение распределительного закона умножения
сложения и вычитания.
8 * 318 = 8 * ( 310 + 8 ) = 2480 + 64 = 2544;
7 * 196 = 7 * ( 200 – 4 ) = 1400 – 28.
2) Произведение двух чисел не изменится, если первый множитель
умножить, а второй разделить на одно и то же натуральное число.
13 * 64 = 26 * 32 = 52 * 16 = …. = 832 * 1;
24 * 17 = (24 * 16) + 24 = ( 48 * 8 ) + 24 = ( 96 * 4 ) + 24 = ( 192 * 2 ) + 24 =
( 384 * 1 ) + 24 = 384 + 24 = 408.
Слайд 323) Метод Ферроля.
Для получения единиц произведения перемножают единицы множителей,
для получения десятков умножают десятки одного на единицы другого
множителя и наоборот и результаты складываются, для получения
сотен перемножают десятки.
Слайд 334) Умножение чисел на 11
Записать последнюю цифру числа, затем
записывать суммы двух соседних цифр множимого и , наконец, первую
цифру множимого.
а) 54 * 11 = 594 1) пишем 4
2) 4 + 5 = 9, пишем 9
3) пишем 5
б) 124 * 11 = 1(1+2)(2+4)4 = 1364
в) 58 * 11 = 638 1) пишем 8
2) 5 + 8 = 13, пишем 3, помним 1
3) 5 + 1 = 6, пишем 6
5) Умножение двузначного числа на 101
Надо приписать справа к данному числу его самого и прочитать
получившееся число.
73 * 101 = 7373
48 * 101 = 4848
6) Умножение на 5, 25, 125
Надо разделить число соответственно на 2, 4, 8 и результат умножить
соответственно на 10, 100, 1000.
а) 46 * 5 = 46 : 2 * 10 = 230;
б) 48 * 25 = 48 : 4 * 100 = 1200;
в) 32 * 125 = 32 : 8 * 1000 = 4000;
г) 53 * 5 = (53 : 2 = 26 и 1-остаток) = 26 * 10 + 1 * 5 = 265;
д) 43 * 25 = (43 : 4 = 10 и 3-остаток) = 10 * 100 + 3 * 25 = 1075;
е) 66 * 125 = (66 : 8 = 8 и 2-остаток) = 8 * 1000 + 2 * 125 = 8250.
Слайд 347) Деление на 5, 25, 125
Надо умножить число соответственно
1000.
а) 220 : 5 = 220 * 2 : 10 = 44;
б) 1300 : 25 = 1300 * 4 : 100 =52;
в) 9250 : 125 = 9250 * 8 : 1000 = 74.
8) Умножение на 9, 99, 999
Надо к первому множителю приписать столько нулей, сколько девяток во втором множителе, затем из результата вычесть первый множитель.
а) 286 * 9 = 2860 – 286 = 2574;
б) 23 * 99 = 2300 – 23 = 2277;
в) 18 * 999 = 1800 – 18 = 17982.
9) Занимательное умножение:
Парад чисел:
11 * 11 = 121
111 * 111 = 12321
1111 * 1111 = 1234321
11111 * 11111 = 123454321
………………………..
111111111 * 111111111 = 12345678987654321
Слайд 35Представить каждое число ( от 1 до 15 ) при помощи
1 = 2 + 2 – 2 – ( 2 : 2); 9 = 2 * 2 * 2 + ( 2 : 2 );
2 = 2 + 2 + 2 – 2 – 2; 10 = 2 + 2 + 2 + 2 + 2;
3 = 2 + 2 – 2 + ( 2 : 2); 11 = 22 : 2 + 2 – 2;
4 = 2 * 2 * 2 – 2 – 2; 12 = 2 * 2 * 2 + 2 + 2;
5 = 2 + 2 + 2 – ( 2 : 2 ); 13 = ( 22 + 2 + 2 ) : 2;
6 = 2 + 2 + 2 + 2 – 2; 14 = 2 * 2 * 2 * 2 – 2;
7 = 22 : 2 – 2 – 2; 15 = 22 : 2 + 2 + 2.
8 = 2 * 2 * 2 + 2 – 2;
Слайд 362. Магические квадраты (сумма чисел вдоль каждой строки, каждого столбца
а) Составь магический квадрат, состоящий из девяти клеток, в которых размещены числа 2, 4, 6, 8, 10, 12, 14, 16, 18 так, чтобы в любом направлении получилось бы число 30.
б) В клетках квадрата переставить числа так, чтобы по всем направлениям
их сумма равна 33.
Слайд 373. Игры
1) Кто первый скажет 100 ?
Двое
Например, первый скажет - 7 , второй – 9, при сложении их получится 16,
затем первый говорит – 5, получится – 21, второй говорит – 8, получится – 29 и т.д. Победителем станет тот, кто первый скажет 100.
2) Не сбейся
В игре участвуют все желающие. Они должны по очереди называть
натуральные числа, которые обладают хотя бы одним из свойств:
а) В записи числа есть цифра 3;
б) Число делится на 3.
Например: 3, 6, 9, 12, 13, 15, 18, 21, 23, 24,…