- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по теме Правильные многогранники
Содержание
- 1. Презентация к уроку по теме Правильные многогранники
- 2. Вопросы1. Какую фигуру называют многогранником?2. Какие многогранники мы рассматривали?3. Какие многогранники я демонстрирую?
- 3. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
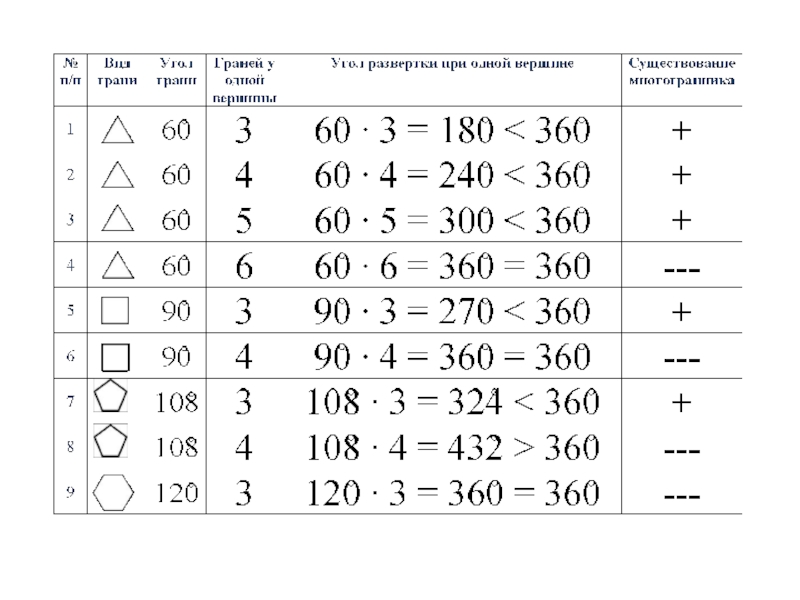
- 4. Ответим на вопросы:Какие многогранники называются правильными?Сколько их существует?Где, зачем и для чего нам нужны многогранники?
- 5. Правильный многогранник - это выпуклый многогранник,
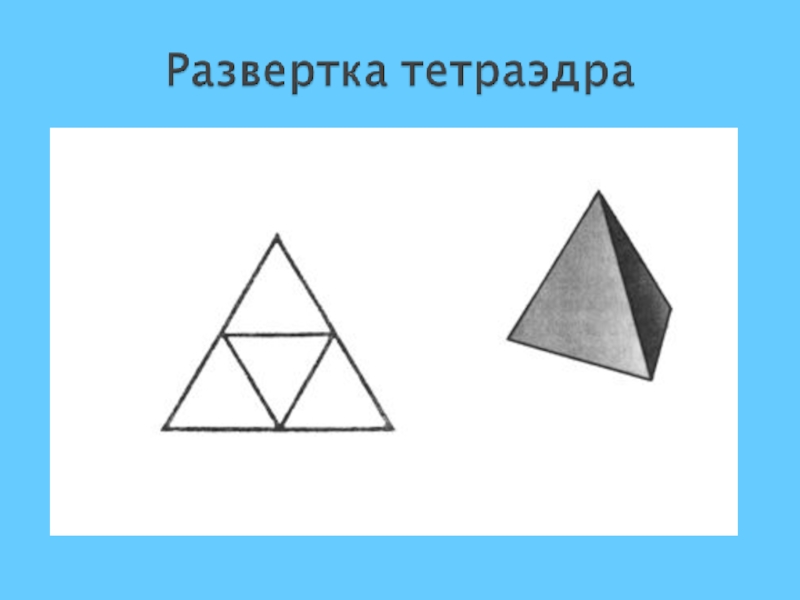
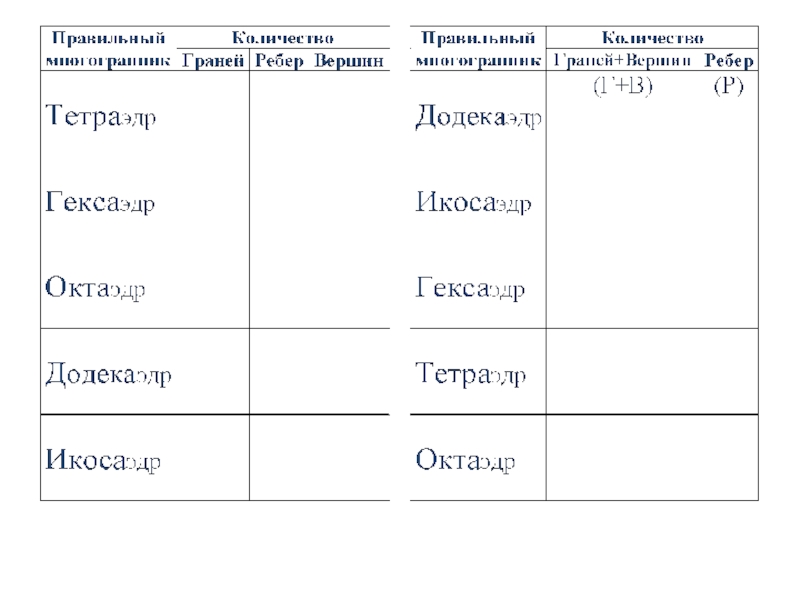
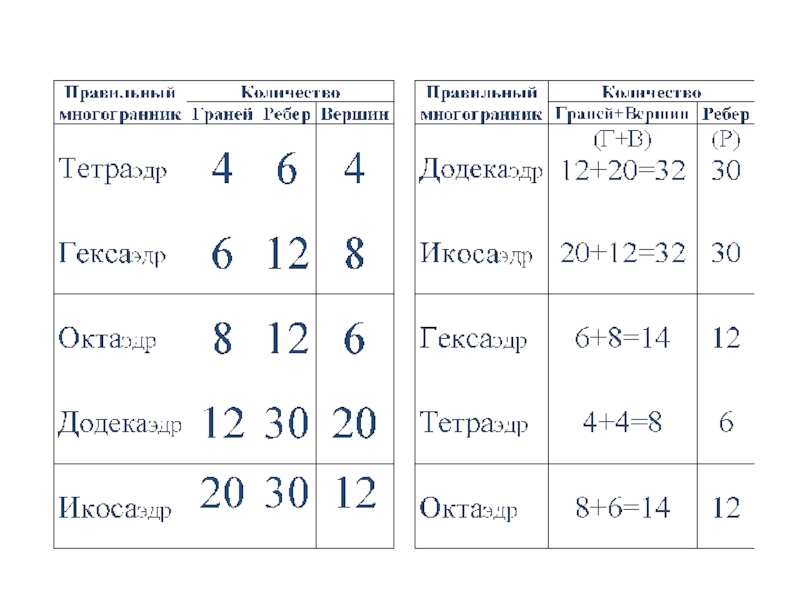
- 6. Тетраэдр простейший многогранник, гранями которого являются четыре треугольника. Вершин – 4,Ребер – 6,Граней – 4.
- 7. Слайд 7
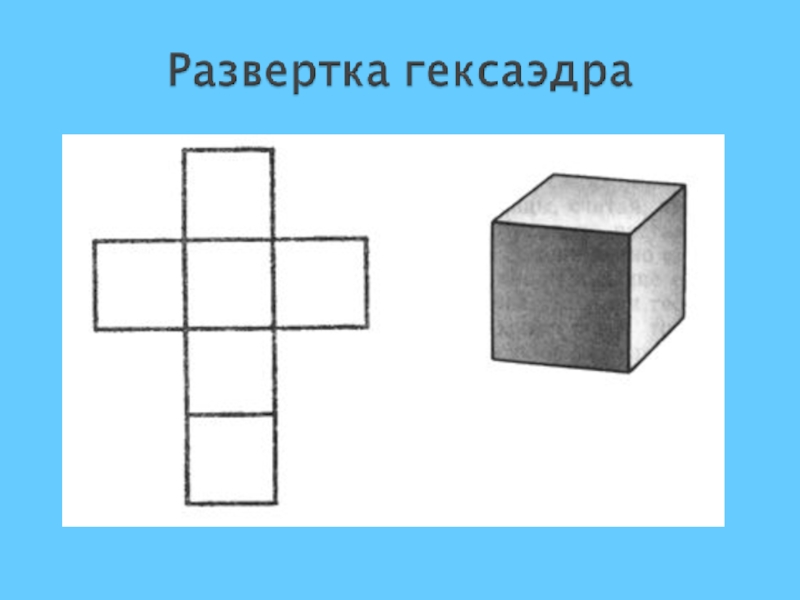
- 8. Гексаэдр (куб)многогранник, гранями которого являются квадраты.Вершин- 8, Ребер – 12,Граней- 6.
- 9. Слайд 9
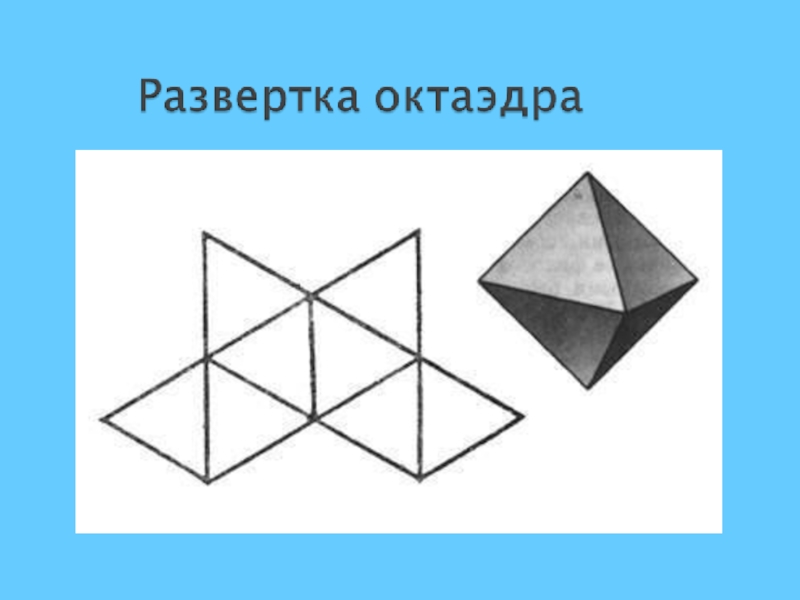
- 10. Октаэдр многогранник, гранями которого являются равносторонние треугольники. Вершин- 6,Ребер – 12,Граней- 8.
- 11. Слайд 11
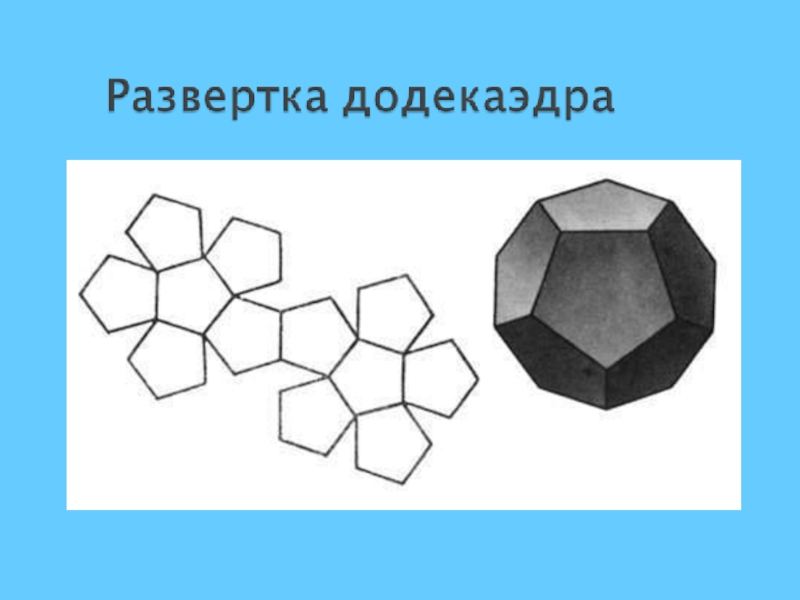
- 12. Додекаэдр многогранник, гранями которого являются правильные пятиугольники.Вершин- 20,Ребер – 30,Граней- 12.
- 13. Слайд 13
- 14. Икосаэдр многогранник, гранями которого являются правильные треугольники.Вершин- 12,Ребер – 30,Граней- 20.
- 15. Слайд 15
- 16. Название указывает на число граней:«эдра» – грань;
- 17. Слайд 17
- 18. Слайд 18
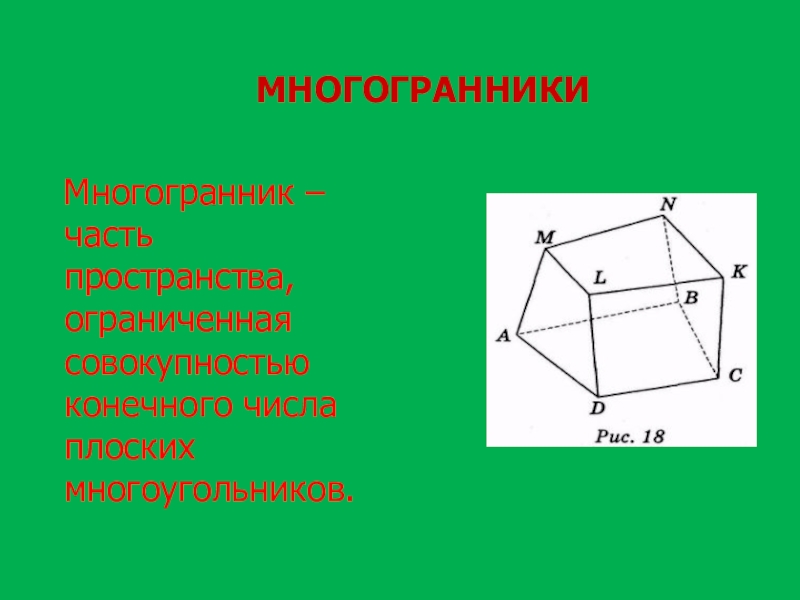
- 19. МНОГОГРАННИКИ Многогранник – часть пространства, ограниченная совокупностью конечного числа плоских многоугольников.
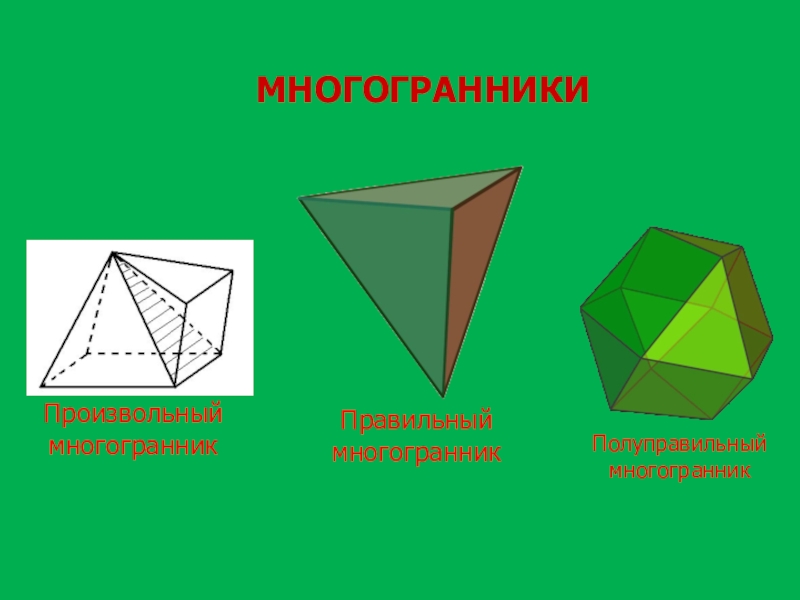
- 20. МНОГОГРАННИКИПолуправильный многогранникПравильный многогранникПроизвольный многогранник
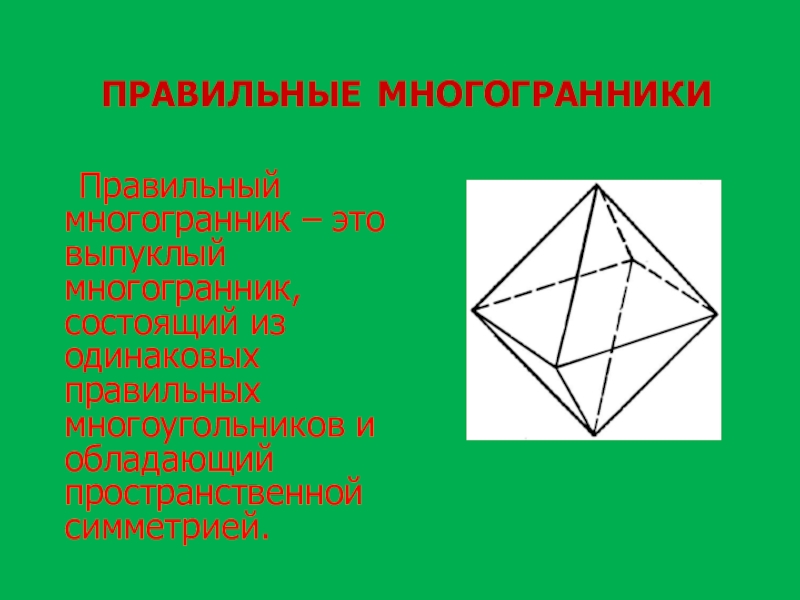
- 21. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ Правильный многогранник – это
- 22. ИСТОРИЯ ПРАВИЛЬНЫХ МНОГОГРАННИКОВЭвклидАрхимедКеплер
- 23. ПРАВИЛЬНЫЕ МНОГОГРАННИКИКосмологическая гипотеза Кеплера
- 24. ПРАВИЛЬНЫЕ МНОГОГРАННИКИТеория В. Макарова и В.Морозова
- 25. ИКОСАЭДРО-ДОДЕКАЭДРОВАЯ МОДЭЛЬ ЗЕМЛИ
- 26. ИСТОРИЯ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ Теэтет Афинский -
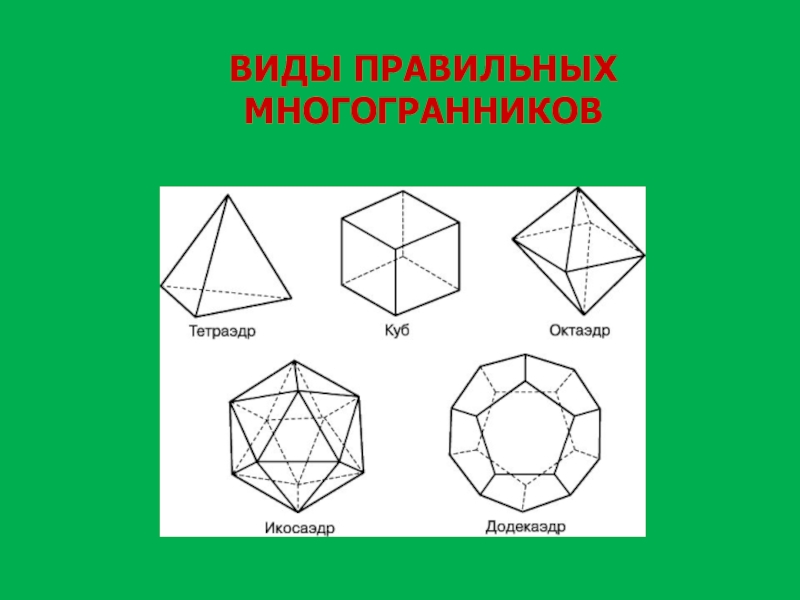
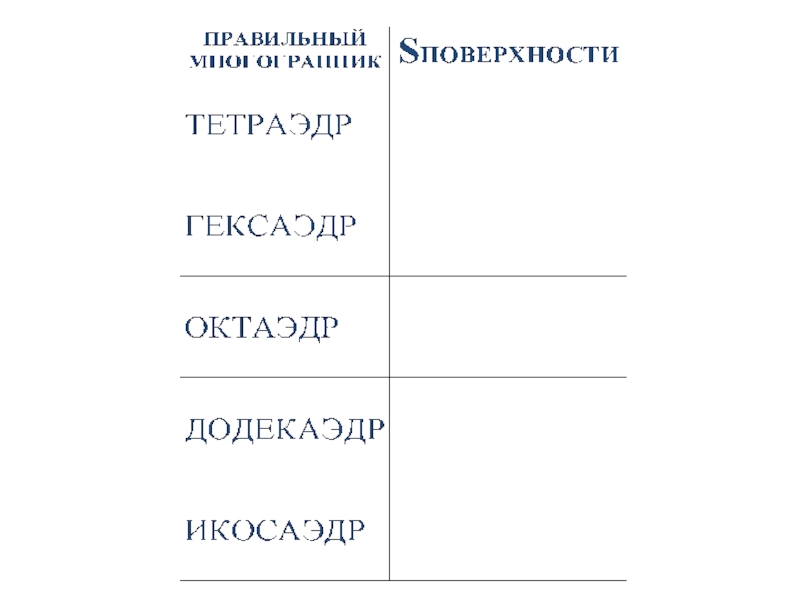
- 27. ВИДЫ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
- 28. СФЕРЫ ПРИМЕНЕНИЯ ПРАВИЛЬНЫХ МНОГОГРАННИКОВНАУКАИСКУССТВОПРИРОДААРХИТЕКТУРА
- 29. «Математика владеет не только истиной, но и
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
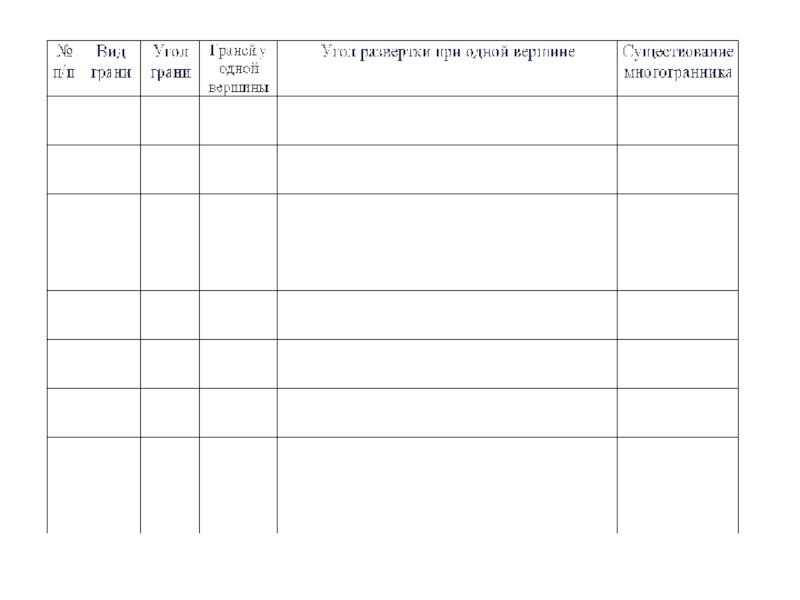
- 34. Результаты практической деятельности
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
- 38. Слайд 38
- 39. Правильные многогранники в искусстве
- 40. Изображения Леонардо да Винчи додекаэдра методом жестких ребер и методом сплошных граней.
- 41. Знаменитый художник, увлекавшийся геометрией, Альбрехт Дюрер(1471- 1528), в известной гравюре «Меланхолия» на переднем плане изобразил додекаэдр.
- 42. Гравюра "Четыре тела" голландский художник Мориц Корнилис Эшер (1898-1972).
- 43. Картина «Тайная Вечеря» художник Сальвадор Дали.
- 44. Между несовместимым всегда есть грань. Но
- 45. Многогранники в архитектуре
- 46. Пирамида Луны. Конец 1 тыс до
- 47. Первое чудо светаПирамида Хеопса, самое грандиозное сооружение на земле. Высота-147 м.
- 48. Фаросский маякВысота маяка составляла 117 метров.Вообще без
- 49. Многогранные башни Смоленской крепостиВ плане крепость имела
- 50. Современнаяархитектура
- 51. Новогодний хрустальный шар в Нью-Йорке обновили к
- 52. Купола Б.Фуллера в современной архитектуреФУЛЛЕР (Fuller) Ричард
- 53. Идея «геодезических куполов» достаточно проста, сфера
- 54. ПОЧЕМУ?Можно ли считать приведенную архитектуру правильными многогранниками?
- 55. Рефлексия
- 56. 1. Как называют многогранники, которые
- 57. СПАСИБО ЗА УРОК!
Вопросы1. Какую фигуру называют многогранником?2. Какие многогранники мы рассматривали?3. Какие многогранники я демонстрирую?
Слайд 2Вопросы
1. Какую фигуру называют многогранником?
2. Какие многогранники мы рассматривали?
3. Какие многогранники
я демонстрирую?
Слайд 4Ответим на вопросы:
Какие многогранники называются правильными?
Сколько их существует?
Где, зачем и для
чего нам нужны многогранники?
Слайд 5Правильный многогранник - это
выпуклый многогранник, все грани которого равные
правильные многоугольники и в каждой вершине которого сходится одно и то же число ребер.
Слайд 6Тетраэдр
простейший многогранник, гранями которого являются четыре треугольника. Вершин – 4,
Ребер
– 6,
Граней – 4.
Граней – 4.
Слайд 8Гексаэдр (куб)
многогранник, гранями которого являются квадраты.
Вершин- 8,
Ребер – 12,
Граней- 6.
Слайд 10Октаэдр
многогранник, гранями которого являются равносторонние треугольники.
Вершин- 6,
Ребер – 12,
Граней-
8.
Слайд 12Додекаэдр
многогранник, гранями которого являются правильные пятиугольники.
Вершин- 20,
Ребер – 30,
Граней- 12.
Слайд 14Икосаэдр
многогранник, гранями которого являются правильные треугольники.
Вершин- 12,
Ребер – 30,
Граней- 20.
Слайд 16Название указывает на число граней:
«эдра» – грань; «тетра» – 4; «гекса»
– 6;
«окта» – 8; «додека» – 12; «икоса» - 20
«окта» – 8; «додека» – 12; «икоса» - 20
Слайд 19МНОГОГРАННИКИ
Многогранник – часть пространства, ограниченная совокупностью конечного числа плоских
многоугольников.
Слайд 21ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Правильный многогранник – это выпуклый многогранник, состоящий из
одинаковых правильных многоугольников и обладающий пространственной симметрией.
Слайд 26ИСТОРИЯ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
Теэтет Афинский - дал математическое описание всем
пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.
Слайд 29
«Математика владеет не только истиной, но и высшей красотой - красотой
отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.»
Бертран Рассел
Бертран Рассел
Слайд 41Знаменитый художник, увлекавшийся геометрией, Альбрехт Дюрер(1471- 1528), в известной гравюре «Меланхолия»
на переднем плане изобразил додекаэдр.
Слайд 44Между несовместимым всегда есть грань. Но иногда эта грань исчезает и
несовместимое сливается в единое целое.
Мне хотелось показать как эта грань исчезает между миром искусства и миром математики.
Слайд 46
Пирамида Луны. Конец 1 тыс до н. э. — начало
н. э. Высота 42 м. Теотиуакан.
Пирамида Кукулькана («Кастильо») в Чичен-Ица. Культура майя. 8-12 вв. Мексика.
Тенаюка. Пирамида 12-15 вв. Культура ацтеков.
Слайд 48Фаросский маяк
Высота маяка составляла 117 метров.
Вообще без геометрии не было бы
ничего. Все здания, которые нас окружают – это геометрические фигуры.
Слайд 49Многогранные башни Смоленской крепости
В плане крепость имела вид неправильной замкнутой фигуры,
которая как бы прижималась к Днепру. В состав крепости входило 38 прясел и столько же башен.
Внизу стена сложена из правильных, хорошо отёсанных прямоугольных блоков белого камня длинной от 92 до 21 сантиметра и высотой от 34 до 20 сантиметров, а вверху из хорошо обожжённого кирпича, средние размеры которого 31х15х6 сантиметров.
Внизу стена сложена из правильных, хорошо отёсанных прямоугольных блоков белого камня длинной от 92 до 21 сантиметра и высотой от 34 до 20 сантиметров, а вверху из хорошо обожжённого кирпича, средние размеры которого 31х15х6 сантиметров.
Слайд 51Новогодний хрустальный шар в Нью-Йорке обновили к 100-летнему юбилею
Теперь шар светит
вдвое ярче, потребляет энергии всего лишь как 20 фенов и, благодаря новым технологиям, имеет 16 миллионов цветовых комбинаций.
Почти двухметровый в диаметре, состоящий из 672 хрустальных треугольников шар заиграл неповторяющимися цветовыми решениями, включая, конечно, звездно-полосатый американский флаг.
Слайд 52Купола Б.Фуллера в современной архитектуре
ФУЛЛЕР (Fuller) Ричард Бакминстер (1895-1983), американский архитектор
и инженер. Разработал легкие и прочные «геодезические купола».
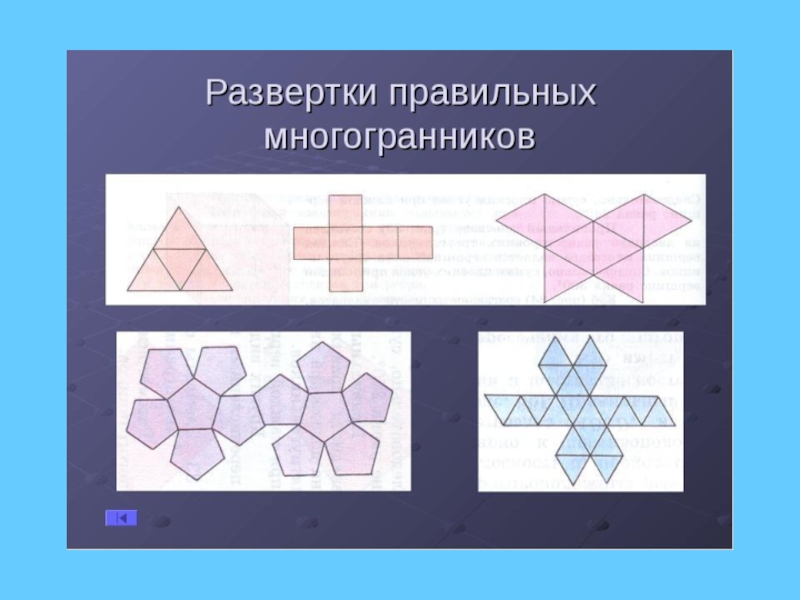
Слайд 53Идея «геодезических куполов» достаточно проста, сфера представляется в виде многогранника (икосаэдра),
то есть двадцатигранника со сторонами в виде правильных треугольников. Эта фигура и разворачивается на плоскость, давая неискаженные соотношения по всей поверхности.
Слайд 56 1. Как называют многогранники, которые ограничены правильными многоугольниками? 2. Какими многоугольниками (по
количеству сторон) могут быть ограничены правильные многогранники?
3. Какие многогранники называются правильными?
4. Перечислите правильные многогранники, с которыми вы сегодня познакомились?
5. Сколько граней у тетраэдра?
6. Сколько граней у октаэдра?
7. Сколько граней у икосаэдра?
8. Как переводится «ЭДРА»?
9. Как зовут твоего преподавателя по математике?
10. Какой из правильных многогранников олицетворяет огонь?