Перестановки и размещения. Факториал.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Перестановки.Факториалы.
Содержание
- 1. Презентация к уроку Перестановки.Факториалы.
- 2. Цели урока- отработать умения решать простейшие комбинаторные
- 3. ЗАДАЧИ УРОКА :
- 4. Задача а) Сколько имеется трехзначных чисел, составленных только из четных цифр?
- 5. Решение Первой цифрой может быть
- 6. б) Сколько имеется трехзначных чисел, кратных 5?Задача
- 7. РешениеПервой цифрой может быть любая цифра, кроме
- 8. Перестановкой из n
- 9. Пример 1. Перестановки из букв
- 10. Факториалn! = п * (п-1)* (п- 2) ... *2 * 1
- 11. Размещением из n элементов по k
- 12. Пример 2.Размещения из букв
- 13. ПерестановкиРn = n!Размещения=
- 14. Задача1 Сколькими способами можно расставить на книжной полке 10 книг для детей ?
- 15. Решение Каждый такой способ это перестановка из
- 16. Задача 2 Пусть даны шесть цифр: 1;
- 17. РешениеЕсли цифры могут повторяться, то количество чисел
- 18. Задача 3
- 19. РешениеРасписание на каждый день может отличаться либо
- 20. Задача 4 В расписании на понедельник
- 21. Решение Рассмотрим алгебру и геометрию
- 22. Задача 5 Сколькими способами 5 мальчиков
- 23. Решение Если мальчики и девочки сядут в
- 24. Задача 6 Сколько различных четырехзначных
- 25. Решение Из цифр 0,
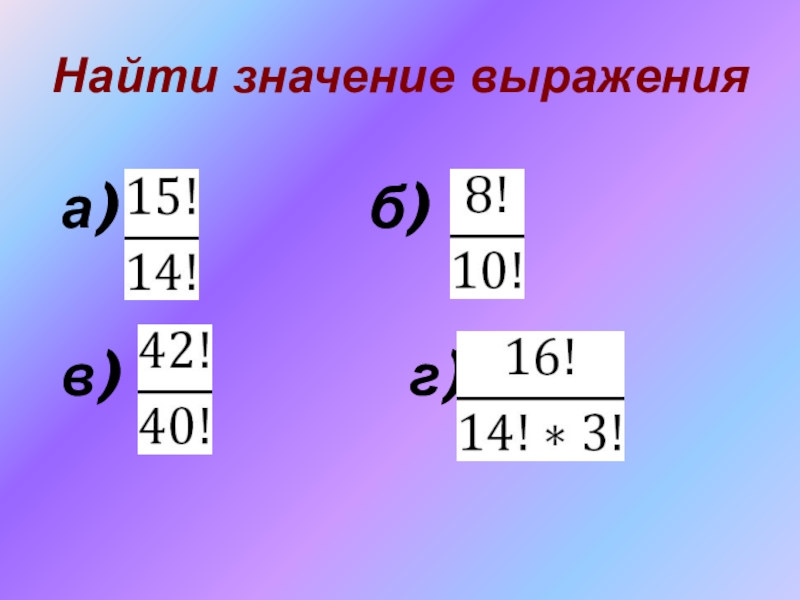
- 26. Найти значение выражения а)
- 27. Ответыа) 15;
- 28. Типичная задача, решаемая с помощью размещений:
- 29. Домашние задания
- 30. Задача 1. 30 книг стоит на
- 31. Задача 3. Делится ли число 30!
- 32. ЛитератураДорофеев Г.В., Суворова С.Б., Шарыгин И.Ф. и
Слайд 1 Работа
Слайд 2Цели урока
- отработать умения решать простейшие комбинаторные задачи с помощью правила
- научить решать задачи с использованием понятий факториала, перестановок и размещений;
Слайд 3
ЗАДАЧИ УРОКА :
образовательные
размещений, факториала;
- ввести формулы для их вычисления;
развивающие
- создать условия для развития логического
мышления и памяти;
- расширять математический кругозор
- развивать навыки научно -
исследовательской деятельности
воспитательные
- воспитывать культуру письма, речи
- формировать чувство ответственности
за принятое решение
Слайд 5Решение
Первой цифрой может быть 2,4, 6 или 8
По правилу умножения получаем ответ: 4·5· 5 = 100.
Слайд 7Решение
Первой цифрой может быть любая цифра, кроме 0, всего 9вариантов. Второй
Третья цифра 0 или 5, тут 2варианта. По правилу умножения получаем ответ: 9·10·2 = 180.
Слайд 8Перестановкой
из n элементов называется комбинация, в
Слайд 11Размещением
из n элементов по k называется комбинация, в которой
Слайд 15Решение
Каждый такой способ
это перестановка из 10
Р10 =10! = 1*2*3*4*5*6*7*8*9*10
= 3638800.
Слайд 16Задача 2
Пусть даны шесть цифр: 1; 2; 3; 4; 5;
Слайд 17Решение
Если цифры могут повторяться, то количество чисел будет
m
Если цифры не повторяются, то
m = = 6 * 5*4 = 120
Слайд 18Задача 3
Студенты института изучают в
Слайд 19Решение
Расписание на каждый день может отличаться либо предметами, либо порядком расположения
= 10 * 9 * 8 = 720
Слайд 20Задача 4
В расписании на понедельник шесть уроков: алгебра, геометрия,
Слайд 21Решение
Рассмотрим алгебру и геометрию как один урок. Тогда
Р5∙Р2=1∙2∙3∙4∙5∙1∙2= 120∙2=240
Слайд 22Задача 5
Сколькими способами 5 мальчиков и 5 девочек могут
Слайд 23Решение
Если мальчики и девочки сядут в произвольном порядке, то способов
Если мальчики сядут на нечетные места, то существуют Р5 способов их расположения. Столькими же способами могут расположиться девочки на четных местах. Каждому способу расположения мальчиков соответствует Р5 способов расположения девочек.
Значит, Р5·Р5=5! ·5!=120·120=14400 способов.
Слайд 24Задача 6
Сколько различных четырехзначных чисел, в которых цифры
0, 2, 4, 6?
Слайд 25Решение
Из цифр 0, 2, 4, 6 можно
Получаем, Р4 – Р3 = 4! – 3! = 24 – 6 =18.
Слайд 28 Типичная задача, решаемая с помощью размещений: Сколькими способами можно выбрать из
Типичная задача решаемая с помощью перестановок: Сколькими способами можно n различных предметов расставить на n различных местах?
Слайд 30 Задача 1. 30 книг стоит на книжной полке, из них
Задача 2. На соревнования по легкой атлетике приехала команда из 12 спортсменок. Сколькими способами тренер может определить, кто из них побежит в эстафете 4×100 м на первом, втором, третьем и четвертом этапах?
Слайд 32Литература
Дорофеев Г.В., Суворова С.Б., Шарыгин И.Ф. и др. Математика. 8-й класс:
Дорофеев Г.В.Математика. 8-й класс: Рабочая тетрадь: К учебнику под редакцией Г.В.Дорофеева, И.Ф.Шарыгина "Математика 6". - М.: Дрофа, 1998.
Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Элементы статистики и теории вероятностей. Учебное пособие для учащихся 7-9 классов общеобразовательных учреждений/ под редакцией Теляковского С.А. – М., «Просвещение», 2003.
Лекции дистанционного курса «Стандарты второго поколения: стохастическая линия элементы комбинаторики, теории вероятностей и статистики в школьном курсе»
Интернет – ресурсы (http//combinatorika.narod.ru/,
http//bankzadach.ru/, http//schol-collection.edu.ru/, и т.д.