- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку наглядной геометрии по теме Кривая Дракона, 6 класс
Содержание
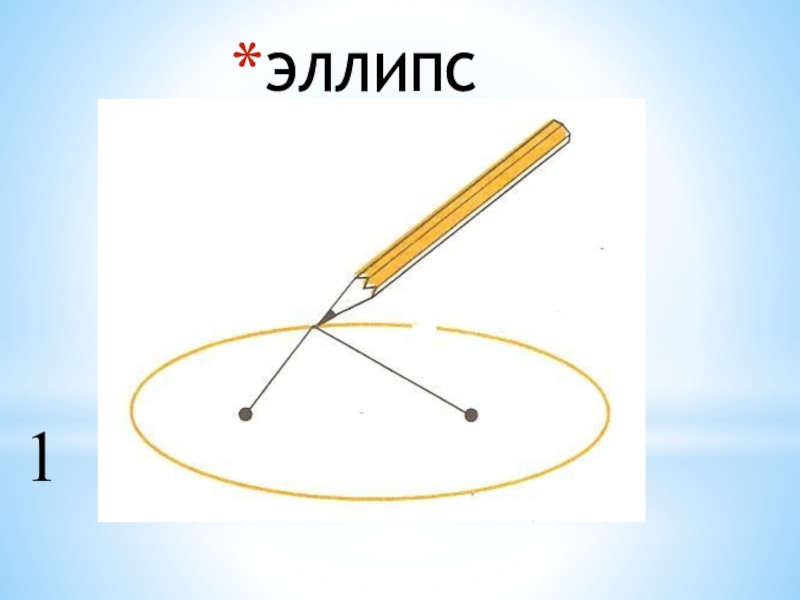
- 1. Презентация к уроку наглядной геометрии по теме Кривая Дракона, 6 класс
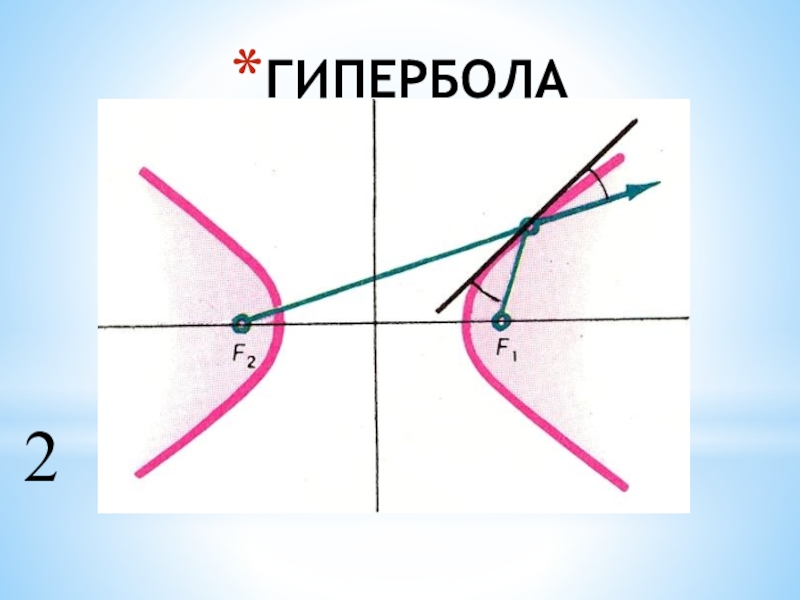
- 2. ГИПЕРБОЛА2
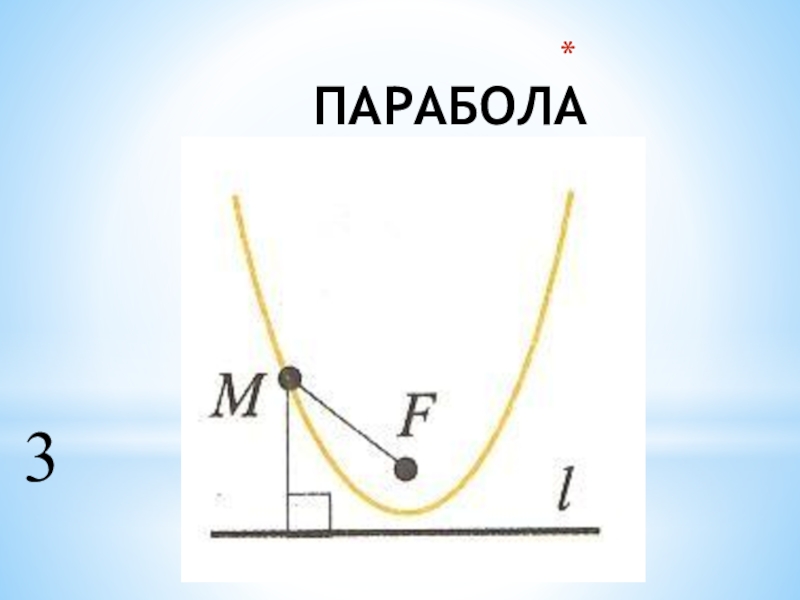
- 3. ПАРАБОЛА 3
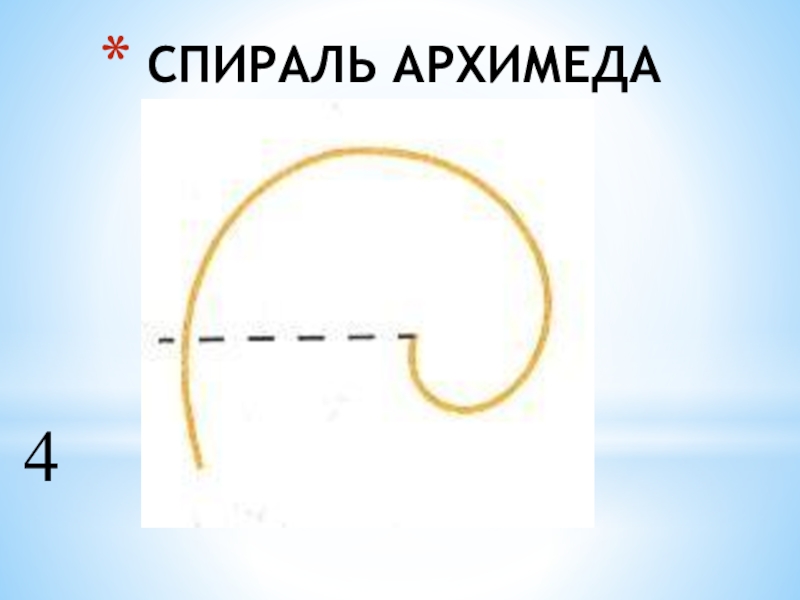
- 4. СПИРАЛЬ АРХИМЕДА4
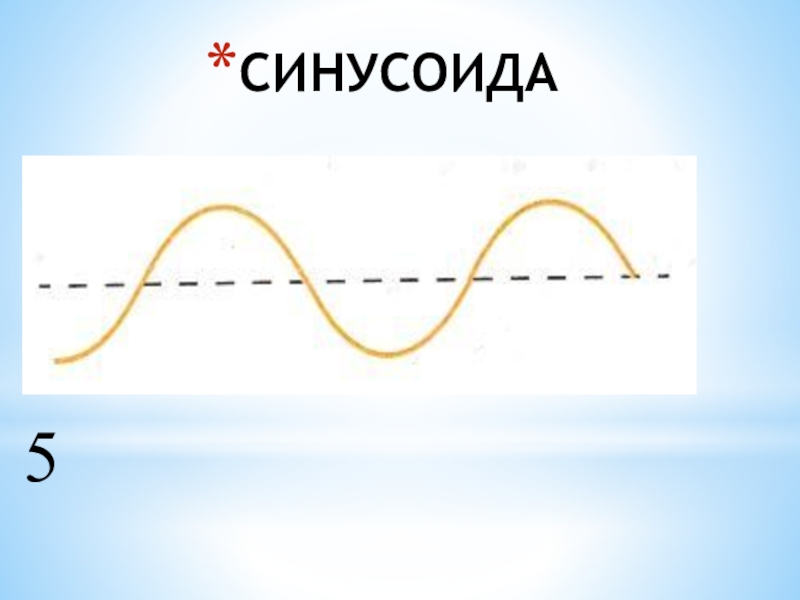
- 5. СИНУСОИДА5
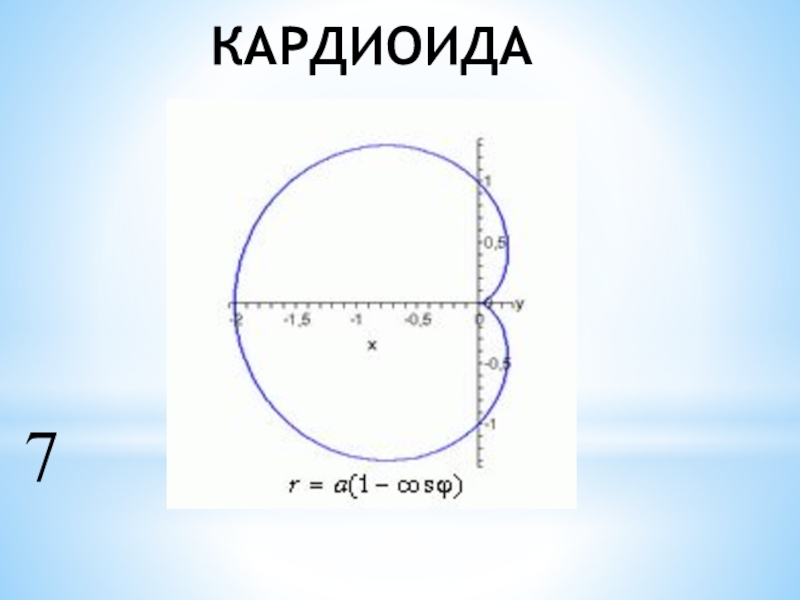
- 6. КАРДИОИДА7
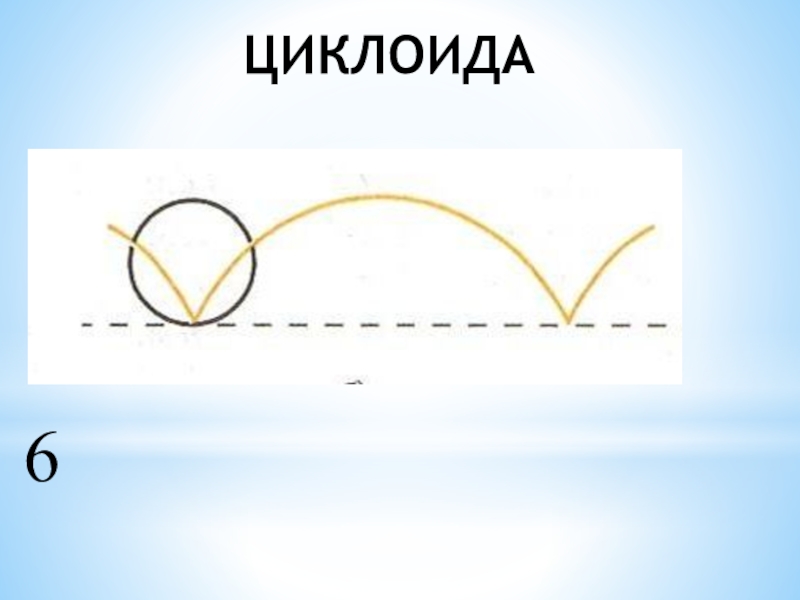
- 7. ЦИКЛОИДА6
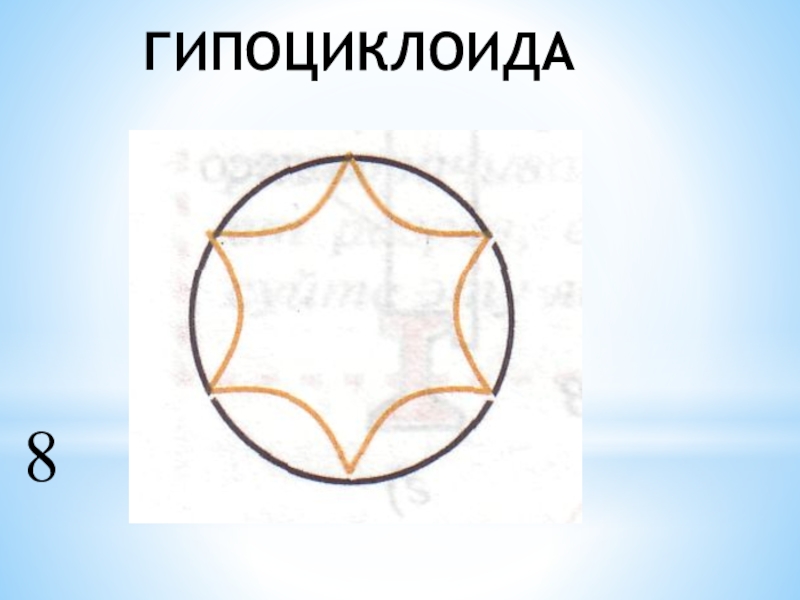
- 8. ГИПОЦИКЛОИДА8
- 9. 9
- 10. Кривая дракона
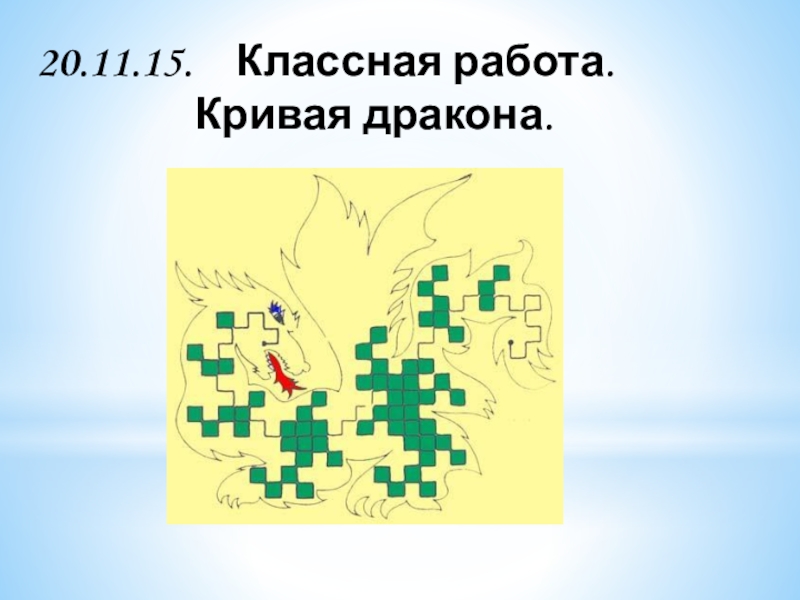
- 11. 20.11.15. Классная работа. Кривая дракона.
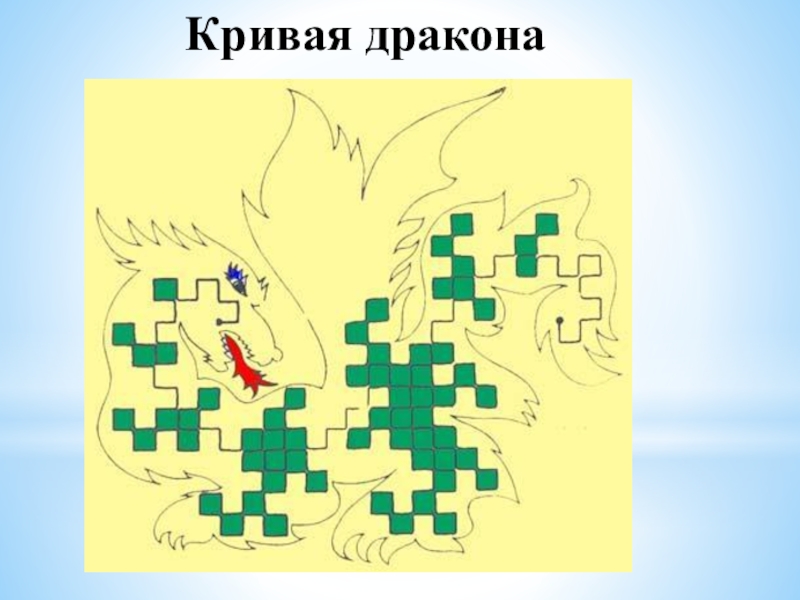
- 12. Кривая, изображенная на рисунке, называется «кривая дракона».
- 13. Кривая дракона впервые была описана в популярной
- 14. «Свои способности человек может узнать, только попытавшись применить их на деле»Сенека
- 15. Возьмите полоску бумаги, длиной двойной лист тетради,
- 16. Изгибы идут в следующем порядке: вниз
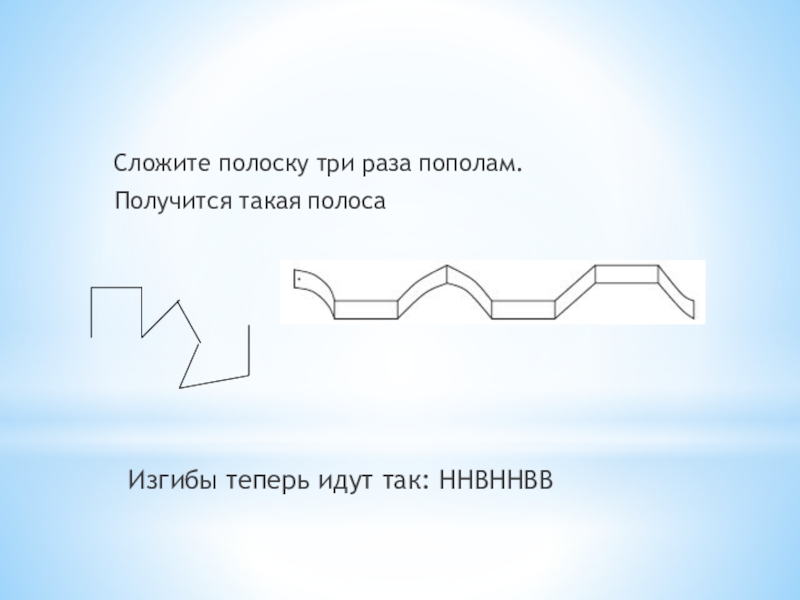
- 17. Сложите полоску три раза пополам. Получится такая полосаИзгибы теперь идут так: ННВННВВ
- 18. Сложите полоску четыре раза и запишите, как
- 19. Коды для рисования кривой Дракона1) Н
- 20. Закономерность:Общее правило для перехода от одного кода к другому:
- 21. Задача 1 Пользуясь этим правилом, напишите цепочку – код для полоски, сложенной в 6 раз.Решение:ННВННВВНННВВНВВНННВННВВВННВВНВВН ННВННВВНННВВНВВВННВННВВВННВВНВВ
- 22. Слайд 22
- 23. Слайд 23
- 24. Задача 2Постройте кривую, соответствующую шести сгибам полоски, из кривой в пять сгибов.
- 25. Задача 3 Возьмите лист бумаги и
- 26. Решение:
ГИПЕРБОЛА2
Слайд 12Кривая, изображенная на рисунке, называется «кривая дракона».
Кривая заключена внутри дракона
и своими изгибами обрисовывает его контур.
Люди, видевшие драконов, подтверждают, что они выглядят именно так.
Придумал ее физик Джон Хейуэй, а подробную теорию разработали Хартер, Хейуэй.
Люди, видевшие драконов, подтверждают, что они выглядят именно так.
Придумал ее физик Джон Хейуэй, а подробную теорию разработали Хартер, Хейуэй.
Слайд 13Кривая дракона впервые была описана в популярной литературе в журнале
Scientific
American в 1967 году.
Заметка о ней появилась в колонке «Математические игры».
Первоначально использовалось полное название кривой «дракон Хартера – Хейтуэя». В дальнейшем стали говорить просто о кривой дракона.
Заметка о ней появилась в колонке «Математические игры».
Первоначально использовалось полное название кривой «дракон Хартера – Хейтуэя». В дальнейшем стали говорить просто о кривой дракона.
Слайд 15 Возьмите полоску бумаги, длиной двойной лист тетради, шириной 5 клеток, левый
конец которой пометьте точкой. Сверните ее пополам, чтобы точка оказалась закрытой, а потом еще пополам (всякий раз правый конец накладываем на левый).
Разверните ее теперь так, чтобы линии сгибов отчетливо выделялись, и положите на стол.
Точка должна быть слева. У вас получилась полоса
Разверните ее теперь так, чтобы линии сгибов отчетливо выделялись, и положите на стол.
Точка должна быть слева. У вас получилась полоса
Слайд 16
Изгибы идут в следующем порядке:
вниз — вниз — вверх.
Или,
вводя обозначения Н — вниз,
В — вверх,это запишется так: Н Н В.
В — вверх,это запишется так: Н Н В.
Слайд 18Сложите полоску четыре раза и запишите, как будут чередоваться изгибы.
ННВННВВНННВВНВВ
Сложите полоску
пять раз и запишите, как будут чередоваться изгибы.
ННВННВВНННВВНВВНННВННВВВННВВНВВ
ННВННВВНННВВНВВНННВННВВВННВВНВВ
Слайд 19 Коды для рисования кривой Дракона
1) Н Н В
2) ННВННВВ
3) ННВННВВНННВВНВВ
4)ННВННВВНННВВНВВНННВННВВВННВВНВВ
Внимательно
посмотрите на них и найдите некоторые закономерности.
Слайд 21Задача 1
Пользуясь этим правилом, напишите цепочку – код для полоски, сложенной
в 6 раз.
Решение:
ННВННВВНННВВНВВНННВННВВВННВВНВВН
ННВННВВНННВВНВВВННВННВВВННВВНВВ
Решение:
ННВННВВНННВВНВВНННВННВВВННВВНВВН
ННВННВВНННВВНВВВННВННВВВННВВНВВ
Слайд 25Задача 3
Возьмите лист бумаги и нарисуйте разноцвет-ными карандашами четырех
Драконов, «выраста-ющих» из одной точки ( у первого Дракона первая черточка идет вверх, у второго – вправо, у треть-его – вниз, у четвертого – влево).