- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку математики по теме Перпендикулярность прямых и плоскостей в пространстве
Содержание
- 1. Презентация к уроку математики по теме Перпендикулярность прямых и плоскостей в пространстве
- 2. Угол между двумя скрещивающимися прямымиПусть прямые a
- 3. Углом между двумя скрещивающимися прямыми называется угол
- 4. Перпендикулярность прямой и плоскостиПрямая называется перпендикулярной плоскости,
- 5. Теорема 3. Две прямые, перпендикулярные одной плоскости, параллельны
- 6. Перпендикуляром, проведенным из данной точки на данную
- 7. Теорема 6. Если из одной точки вне плоскости
- 8. Перпендикулярность двух плоскостейПусть прямая a является линией
- 9. Теорема 8. Признак перпендикулярности двух плоскостей. Пусть a перпендикулярна α,
- 10. Перпендикулярность прямых и плоскостей. Теорема об общем
- 11. Угол между наклонной и плоскостьюУглом между наклонной
- 12. На чертеже показана наклонная AB, OB = Пр α AB,
- 13. Двугранный уголДвугранный угол – это часть пространства, заключенная между двумя полуплоскостями, имеющими одну общую границу.
- 14. Полуплоскости α и β, образующие двугранный угол,
- 15. При пересечении двух плоскостей образуются четыре двугранных
- 16. Ортогональное проектированиеПараллельное проектирование, при котором проектирующие прямые
- 17. Первый случай. Плоскость проекции проходит через сторону
- 18. Второй случай. Ни одна сторона Δ ABC не
- 19. Третий случай. Плоскость Δ перпендикулярна плоскости проекции.
- 20. ПрименениеПерпендикулярность прямых и плоскостей широко используется в
Слайд 1Перпендикулярность прямых и плоскостей в пространстве. Разработка урока – лекции. Учитель математики Кураховской гимназии
Слайд 2Угол между двумя скрещивающимися прямыми
Пусть прямые a и b скрещивающиеся. Выберем
Слайд 3Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми,
Две прямые в пространстве называются перпендикулярными, если они образуют прямой угол. На чертеже изображен куб ABCDA1B1C1D1. Скрещивающиеся прямые A1D1 и CD перпендикулярны. Действительно, A1D1 перпендикулярно C1D1, а C1D1 || CD.
Назовем еще несколько пар скрещивающихся перпендикулярных прямых: A1D1 и AB, A1B1 и BC, A1B1 и AD, B1C1 и AB
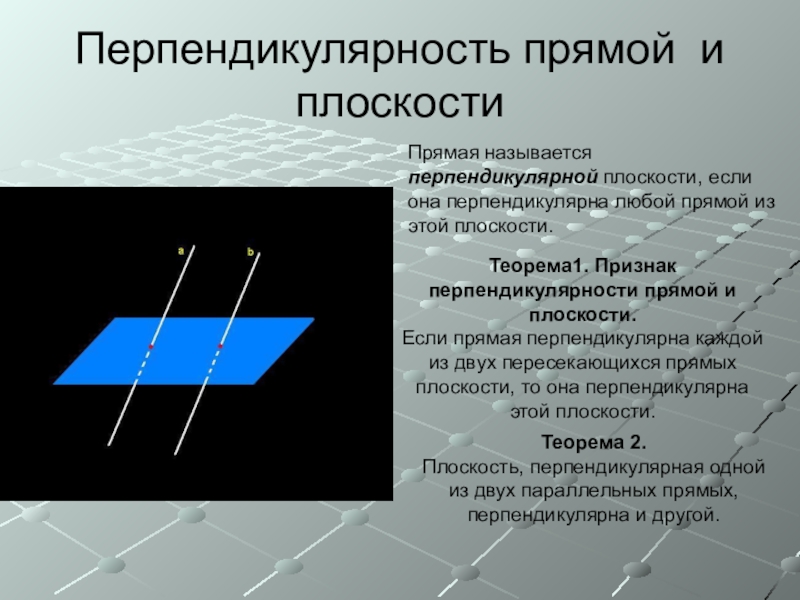
Слайд 4Перпендикулярность прямой и плоскости
Прямая называется перпендикулярной плоскости, если она перпендикулярна любой
Теорема1. Признак перпендикулярности прямой и плоскости.
Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.
Теорема 2.
Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой.
Слайд 5Теорема 3.
Две прямые, перпендикулярные одной плоскости, параллельны между собой.
Теорема 4.
Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой.
Теорема 5.
Две плоскости, перпендикулярные одной прямой, параллельны между собой.
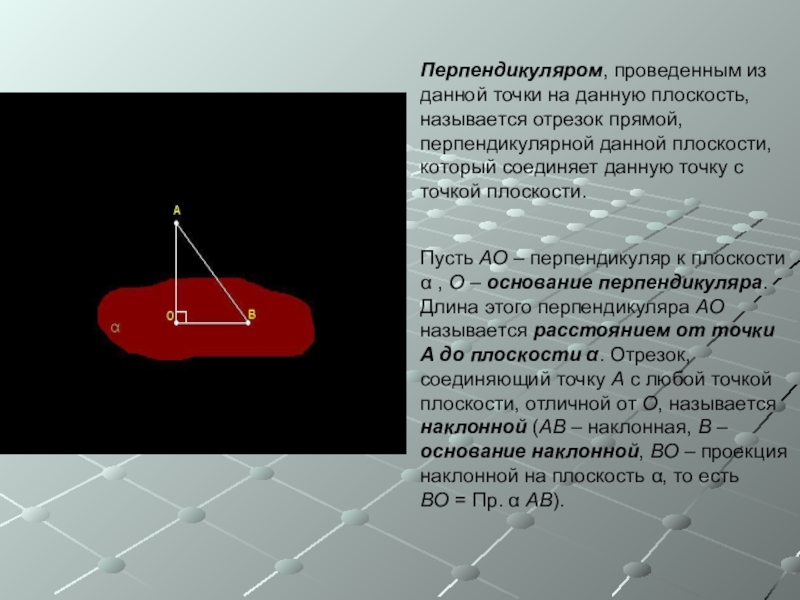
Слайд 6Перпендикуляром, проведенным из данной точки на данную плоскость, называется отрезок прямой,
Пусть AO – перпендикуляр к плоскости α , O – основание перпендикуляра. Длина этого перпендикуляра AO называется расстоянием от точки A до плоскости α. Отрезок, соединяющий точку A с любой точкой плоскости, отличной от O, называется наклонной (AB – наклонная, B – основание наклонной, BO – проекция наклонной на плоскость α, то есть BO = Пр. α AB).
Слайд 7Теорема 6.
Если из одной точки вне плоскости проведены к ней перпендикуляр
длина перпендикуляра меньше длины любой наклонной;
наклонные с равными проекциями равны;
из двух наклонных большую длину имеет та, у которой больше проекция.
Теорема 7. О трех перпендикулярах.
Для того, чтобы прямая на плоскости была перпендикулярна наклонной, необходимо и достаточно, чтобы эта прямая была перпендикулярна ортогональной проекции наклонной на плоскость.
Слайд 8Перпендикулярность двух плоскостей
Пусть прямая a является линией пересечения плоскостей α и
Это определение не зависит от плоскости γ. Действительно, если провести другую плоскость δ, перпендикулярную прямой a, то δ || γ.
Пусть δ пересекает α по m', δ пересекает β по n'. По теореме о следах m' || m и n' || n. Угол, образованный прямыми m' и n', и угол, образованный прямыми m и n, равны как углы с соответственно параллельными и одинаково направленными сторонами.
Слайд 9Теорема 8. Признак перпендикулярности двух плоскостей.
Пусть a перпендикулярна α, a принадлежит β, тогда β перпендикулярна α.
Теорема 9.
Пусть α перпендикулярна β, α пересекает β по прямой a, b перпендикулярна a, b принадлежит β, тогда b перпендикулярна α. То есть прямая b, лежащая в одной из взаимно перпендикулярных плоскостей β и перпендикулярная линии пересечения a этих плоскостей, перпендикулярна и другой плоскости α.
Теорема 10.
Если плоскости α и β взаимно перпендикулярны, и к плоскости α проведен перпендикуляр, имеющий общую точку с плоскостью β, то этот перпендикуляр лежит в плоскости β.
Теорема 11.
Пусть плоскости α и β перпендикулярны плоскости γ и пересекаются по прямой a, тогда a перпендикулярна γ.
Слайд 10Перпендикулярность прямых и плоскостей. Теорема об общем перпендикуляре двух скрещивающихся прямых
Общим
Теорема 12.
Две скрещивающиеся прямые имеют общий перпендикуляр, и притом единственный.
Лемма 1.
Две скрещивающиеся прямые лежат в параллельных плоскостях.
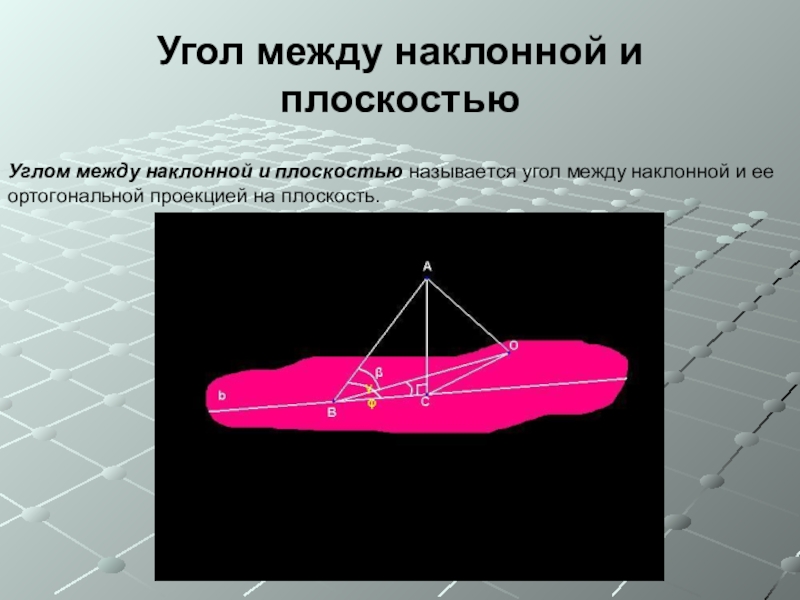
Слайд 11Угол между наклонной и плоскостью
Углом между наклонной и плоскостью называется угол
Слайд 12На чертеже показана наклонная AB, OB = Пр α AB, ABO – угол
Заметим, что или
Мы получили формулу трех косинусов. Обратите внимание на то, что плоскости углов β и γ взаимно перпендикулярны.
Замечание. Поскольку углы φ, β и γ острые, из формулы трех косинусов следует, что cos β > cos φ и 0° < β < φ.
Таким образом, углом β между наклонной и ее ортогональной проекцией на плоскость является наименьший из углов, образованных наклонной с прямыми плоскости α.
Слайд 13Двугранный угол
Двугранный угол – это часть пространства, заключенная между двумя полуплоскостями,
Слайд 14Полуплоскости α и β, образующие двугранный угол, называются его гранями. Общая
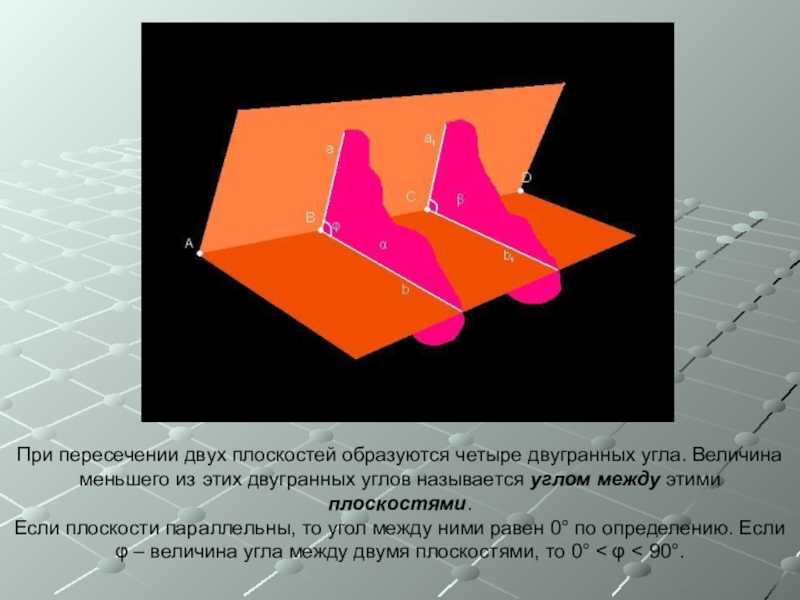
Слайд 15При пересечении двух плоскостей образуются четыре двугранных угла. Величина меньшего из
Если плоскости параллельны, то угол между ними равен 0° по определению. Если φ – величина угла между двумя плоскостями, то 0° < φ < 90°.
Слайд 16Ортогональное проектирование
Параллельное проектирование, при котором проектирующие прямые перпендикулярны к плоскости проекций,
Теорема 13.
Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции:
Доказательство
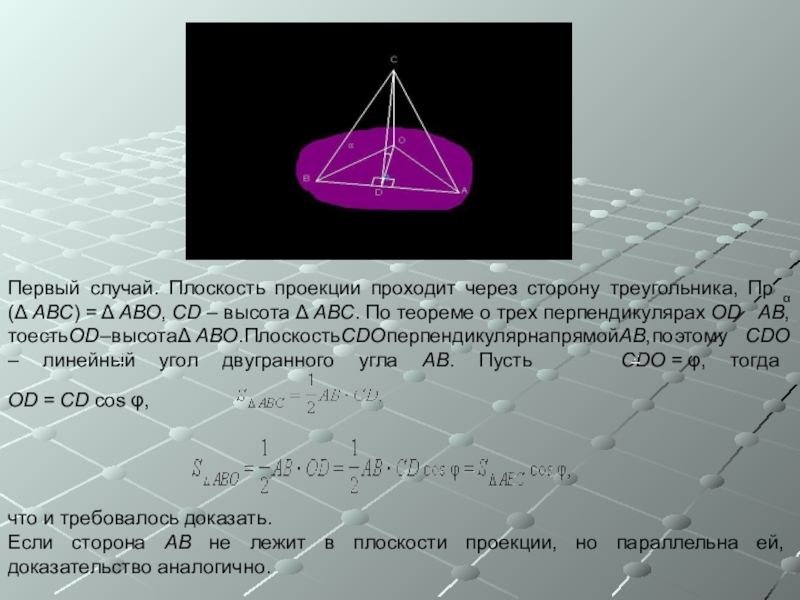
Слайд 17Первый случай. Плоскость проекции проходит через сторону треугольника, Пр α(Δ ABC) = Δ ABO, CD
что и требовалось доказать.
Если сторона AB не лежит в плоскости проекции, но параллельна ей, доказательство аналогично.
Слайд 18Второй случай. Ни одна сторона Δ ABC не параллельна плоскости проекции. Проведем
Складывая или вычитая эти равенства в зависимости от того принадлежит точка D отрезку AC или лежит вне него, имеем
что и требовалось доказать.
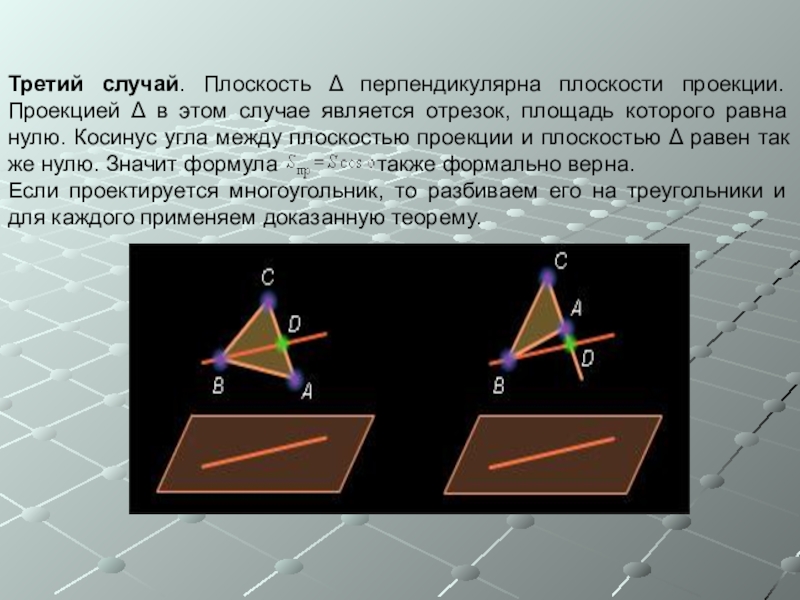
Слайд 19Третий случай. Плоскость Δ перпендикулярна плоскости проекции. Проекцией Δ в этом
Если проектируется многоугольник, то разбиваем его на треугольники и для каждого применяем доказанную теорему.
Слайд 20Применение
Перпендикулярность прямых и плоскостей широко используется в строительной промышленности (для правильности
В инженерно-технических проектах, где перпендикулярность прямых и плоскостей является основой для построений более сложных элементов.