СОШ №2033
г.Москва
руководитель учитель математики Жижкина И.Л.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к проекту Геометрическая прогрессия
Содержание
- 1. Презентация к проекту Геометрическая прогрессия
- 2. Геометрическая прогрессияЦель: изучить применение геометрической прогрессии в математике и жизни
- 3. Геометрическая прогрессияЛегенда о шахматахХронологическая лента изучения прогрессииТеория вопросаПрогрессия вокруг насСтаринные задачи на прогрессию
- 4. Геометрическая прогрессияДавным-давно, более 1500 лет назад, в
- 5. Геометрическая прогрессияОпрос одноклассниковСколько зерна выдал Раджа мудрецу
- 6. Геометрическая прогрессияХронологическая лента изученияоколо 2000 г. до
- 7. Геометрическая прогрессияТеория вопросаПоследовательности. Рассмотрим ряд натуральных чисел: 1, 2,
- 8. Геометрическая прогрессияПрогрессия вокруг нас
- 9. Геометрическая прогрессияПрогрессия вокруг насБыстрота размножения бактерий
- 10. Геометрическая прогрессияСтаринные задачи на прогрессиюСамый большой, сохранившийся
- 11. Слайд 11
- 12. Геометрическая прогрессияСтаринные задачи на прогрессиюРусский математик и
- 13. Геометрическая прогрессияСтаринные задачи на прогрессиюНекто продал лошадь
- 14. ВыводГеометрическая прогрессия постоянно встречается и используется не
- 15. БЛАГОДАРЮ ЗА ВНИМАНИЕ!
Геометрическая прогрессияЦель: изучить применение геометрической прогрессии в математике и жизни
Слайд 2Геометрическая прогрессия
Цель: изучить применение геометрической прогрессии в математике и жизни
Слайд 3Геометрическая прогрессия
Легенда о шахматах
Хронологическая лента изучения прогрессии
Теория вопроса
Прогрессия вокруг нас
Старинные задачи
на прогрессию
Слайд 4Геометрическая прогрессия
Давным-давно, более 1500 лет назад, в Индии правил жадный и
жестокий властелин — раджа Схерм. Своей гордыней, нежеланием слушать советы приближенных он довел свое государство до разорения. Тогда придворный мудрец Сесса, сын Дагера, осторожно, чтобы не рассердить правителя, в качестве намека придумал игру, в которой было видно, что один правитель без помощников ничего не стоит. Это была игра в шахматы.
Радже игра очень понравилась, и он предложил изобретателю любую награду. Каково же было удивление властелина, когда мудрец попросил не богатства, не земли, а пшеничных зерен — столько, сколько покажут клетки шахматной доски. На первую клетку требовалось положить 1 зерно, на вторую — два, и на каждую последующую — в два раза больше, чем на предыдущую.
Раджа подивился такой странной просьбе и, усмехнувшись, велел принести мудрецу два мешка пшеницы. Но когда зерна стали выкладывать на клетки доски, оказалось, что их не хватает.
Чтобы расплатиться с создателем игры, радже нужно было отдать 18 квинтильонов 446 квадрильонов 744 триллиона 73 миллиарда 709 миллионов 551 тысячу 615 штук зерен пшеницы.
Этого зерна хватило бы, чтобы 8 раз засеять всю землю и 8 раз собрать урожай.
Раджа был так поражен, что вынужден был усомниться во всегдашней правильности своих решений и с тех пор прислушивался к советам своих приближенных.
Радже игра очень понравилась, и он предложил изобретателю любую награду. Каково же было удивление властелина, когда мудрец попросил не богатства, не земли, а пшеничных зерен — столько, сколько покажут клетки шахматной доски. На первую клетку требовалось положить 1 зерно, на вторую — два, и на каждую последующую — в два раза больше, чем на предыдущую.
Раджа подивился такой странной просьбе и, усмехнувшись, велел принести мудрецу два мешка пшеницы. Но когда зерна стали выкладывать на клетки доски, оказалось, что их не хватает.
Чтобы расплатиться с создателем игры, радже нужно было отдать 18 квинтильонов 446 квадрильонов 744 триллиона 73 миллиарда 709 миллионов 551 тысячу 615 штук зерен пшеницы.
Этого зерна хватило бы, чтобы 8 раз засеять всю землю и 8 раз собрать урожай.
Раджа был так поражен, что вынужден был усомниться во всегдашней правильности своих решений и с тех пор прислушивался к советам своих приближенных.
Легенда
о шахматах
Слайд 5Геометрическая прогрессия
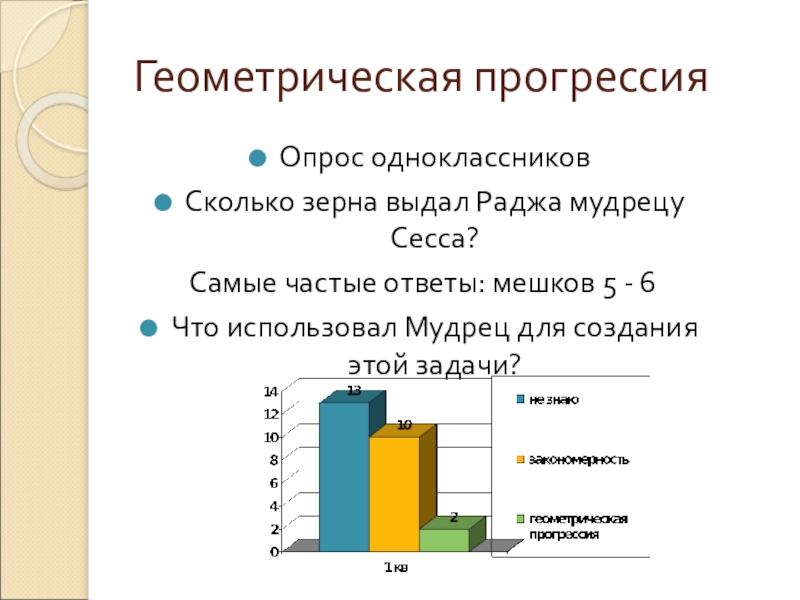
Опрос одноклассников
Сколько зерна выдал Раджа мудрецу Сесса?
Самые частые ответы: мешков
5 - 6
Что использовал Мудрец для создания этой задачи?
Что использовал Мудрец для создания этой задачи?
Слайд 6Геометрическая прогрессия
Хронологическая лента изучения
около 2000 г. до н.э - Введен термин
прогрессия автором Боэцием
III век до н.э -Древнегреческий папирус Ахмеса
ХVI век - Правило для суммирования любой бесконечной
убывающей геометрической прогрессии
1484 год - Формула суммы членов геометрической прогрессии
Слайд 7Геометрическая прогрессия
Теория вопроса
Последовательности. Рассмотрим ряд натуральных чисел:
1, 2, 3, … , n – 1, n ,
… .
Если заменить каждое число n в этом ряду некоторым числом un , следуя некоторому закону, мы получим новый ряд чисел:
u1 , u2 , u3 , …, u n - 1 , u n , … ,
называемый числовой последовательностью. Число un называется общим членом числовой последовательности.
П р и м е р ы числовых последовательностей:
2, 4, 6, 8, 10, … , 2n, … ;
1, 4, 9, 16, 25, … , n² , … ;
1, 1/2, 1/3, 1/4, 1/5, … , 1/n , … .
Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на постоянное для этой последовательности число q , называется геометрической прогрессией.
Число q называется знаменателем прогрессии. Любой член геометрической прогрессии вычисляется по формуле: bn = b1 q n - 1 .
Сумма n первых членов геометрической прогрессии вычисляется как:
Если заменить каждое число n в этом ряду некоторым числом un , следуя некоторому закону, мы получим новый ряд чисел:
u1 , u2 , u3 , …, u n - 1 , u n , … ,
называемый числовой последовательностью. Число un называется общим членом числовой последовательности.
П р и м е р ы числовых последовательностей:
2, 4, 6, 8, 10, … , 2n, … ;
1, 4, 9, 16, 25, … , n² , … ;
1, 1/2, 1/3, 1/4, 1/5, … , 1/n , … .
Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на постоянное для этой последовательности число q , называется геометрической прогрессией.
Число q называется знаменателем прогрессии. Любой член геометрической прогрессии вычисляется по формуле: bn = b1 q n - 1 .
Сумма n первых членов геометрической прогрессии вычисляется как:
Слайд 10Геометрическая прогрессия
Старинные задачи на прогрессию
Самый большой, сохранившийся до наших дней, древнеегипетский
математический текст - это так называемый папирус писца Ахмеса (ок. 1650 до н. э.). Папирус имеет размер 5,25 м х 33 см и содержит 84 задачи. Папирус был приобретен в 1858 г. Г.Райндом и изучен впервые профессором А. Эйзенлором в 1877 г. Другой папирус (5,44 м х 8 см) включает 25 задач. Он был приобретен русским востоковедом В.С. Голенищевым в 1893 г. и в настоящее время принадлежит Московскому музею изобразительных искусств им. А.С. Пушкина. Московский папирус исследовали ученые - академики Б.А. Тураев и В.В. Струве.
Вот задача.
Задача 1. У семи лиц по 7 кошек, каждая кошка съедает 7 мышей, каждая мышь съедает 7 колосьев, каждый колос даёт 7 растений, на каждом растении вырастает 7 мер зерна. Как велики числа этого ряда и их сумма?
Вот задача.
Задача 1. У семи лиц по 7 кошек, каждая кошка съедает 7 мышей, каждая мышь съедает 7 колосьев, каждый колос даёт 7 растений, на каждом растении вырастает 7 мер зерна. Как велики числа этого ряда и их сумма?
Слайд 12Геометрическая прогрессия
Старинные задачи на прогрессию
Русский математик и педагог Леонтий Филиппович Магницкий
в 1703 г. опубликовал в Москве свою знаменитую книгу
“Арифметика, сиречь наука числительная”, которая до середины XVIII в. была основным учебником по математике в России. Решите приведенную в ней забавную задачу.
“Арифметика, сиречь наука числительная”, которая до середины XVIII в. была основным учебником по математике в России. Решите приведенную в ней забавную задачу.
Слайд 13Геометрическая прогрессия
Старинные задачи на прогрессию
Некто продал лошадь за 156 рублей. Но
покупатель, приобретая лошадь, раздумал ее покупать и возвратил продавцу, говоря: - Нет мне расчета покупать за эту цену лошадь, которая таких денег не стоит. Тогда продавец предложил другие условия:
- Если по-твоему, цена лошади высока, то купи ее подковные гвозди; лошадь же тогда получишь в придачу бесплатно. Гвоздей в каждой подкове 6. За первый гвоздь дай мне всего ¼ коп., за второй ½ коп., за третий 1 коп. и т.д
Покупатель, соблазненный низкой ценой и желая даром получить лошадь, принял условие продавца, рассчитывая, что за гвозди придется уплатить не более 10 рублей.
На сколько покупатель проторговался?
Количество подков: 4
Количество гвоздей: 6*4=24 n = 24
Первый гвоздь: ¼ копейки b1 = 1/4
Второй гвоздь: ½ копейки q = 2
- Если по-твоему, цена лошади высока, то купи ее подковные гвозди; лошадь же тогда получишь в придачу бесплатно. Гвоздей в каждой подкове 6. За первый гвоздь дай мне всего ¼ коп., за второй ½ коп., за третий 1 коп. и т.д
Покупатель, соблазненный низкой ценой и желая даром получить лошадь, принял условие продавца, рассчитывая, что за гвозди придется уплатить не более 10 рублей.
На сколько покупатель проторговался?
Количество подков: 4
Количество гвоздей: 6*4=24 n = 24
Первый гвоздь: ¼ копейки b1 = 1/4
Второй гвоздь: ½ копейки q = 2
Слайд 14Вывод
Геометрическая прогрессия постоянно встречается и используется не только в математике, но
и в жизни, но мало людей знают о ней. Думаю, что мне и моим одноклассником очень интересно будет познакомиться с геометрической прогрессией на уроках математики