Выполнил: Зубаков Юрий, обучающийся 5 класса;
Руководитель: Тляубаева З.И.,учитель математики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к исследовательской работе Магические квадраты
Содержание
- 1. Презентация к исследовательской работе Магические квадраты
- 2. «Далёкое время Застыло на камне, А мы
- 3. ”Я не знаю ничего более прекрасного в арифметике,
- 4. Слайд 4
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Гипотеза:Изучение свойств магических квадратов даст возможность любому построить этот квадрат.
- 9. Цели и задачи моей работы: изучить историю возникновения
- 10. Из истории развития магических квадратовМагические квадраты возникли
- 11. Слайд 11
- 12. Из истории развития магических квадратов
- 13. Магический квадрат-это квадрат, сумма чисел которого
- 14. Магический квадрат 2х2Магических квадратов 2х2 не существует.
- 15. Как ни расставляй числа в клетках таблицы,
- 16. Магический квадрат 3х3 только одинНайдем сумму чисел
- 17. 1.Из магического квадрата можно получить новый, с
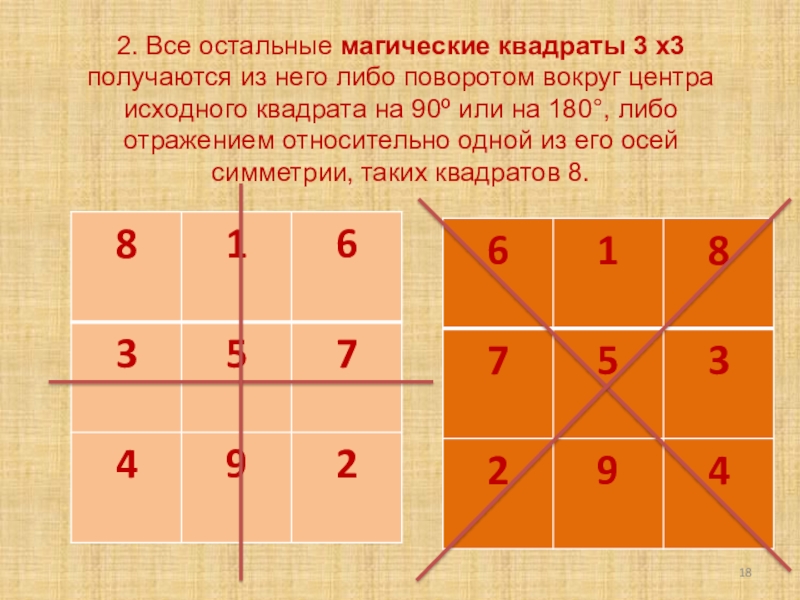
- 18. 2. Все остальные магические квадраты 3 х3
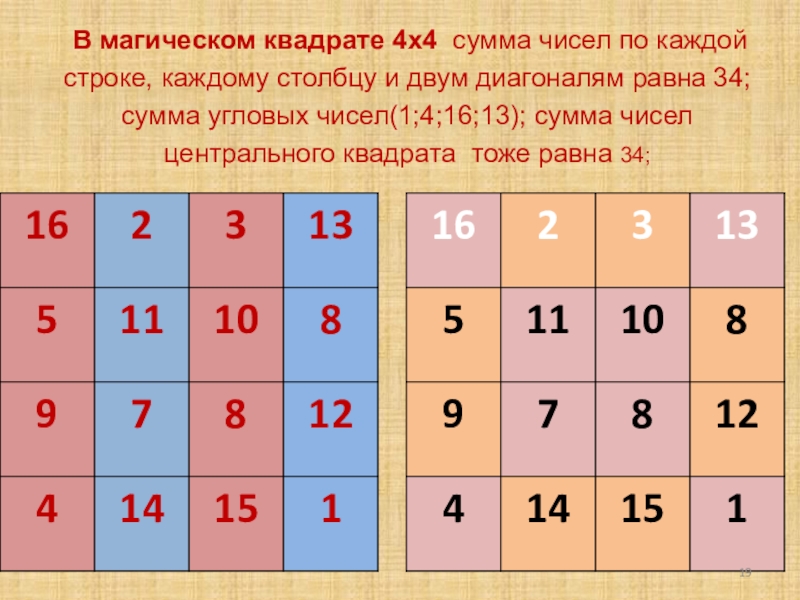
- 19. В магическом квадрате 4х4 сумма чисел
- 20. Сумма цифр в каждом квадрате 2х2 равна
- 21. Это знаменитый магический квадрат Дюрера.
- 22. Магический квадрат 5х5Суммы пятерок чисел на разломанных
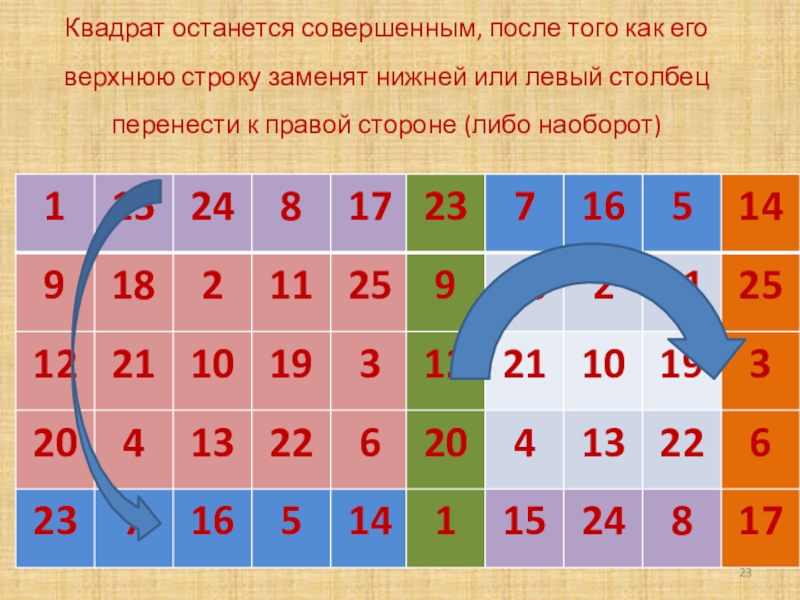
- 23. Квадрат останется совершенным, после того как его
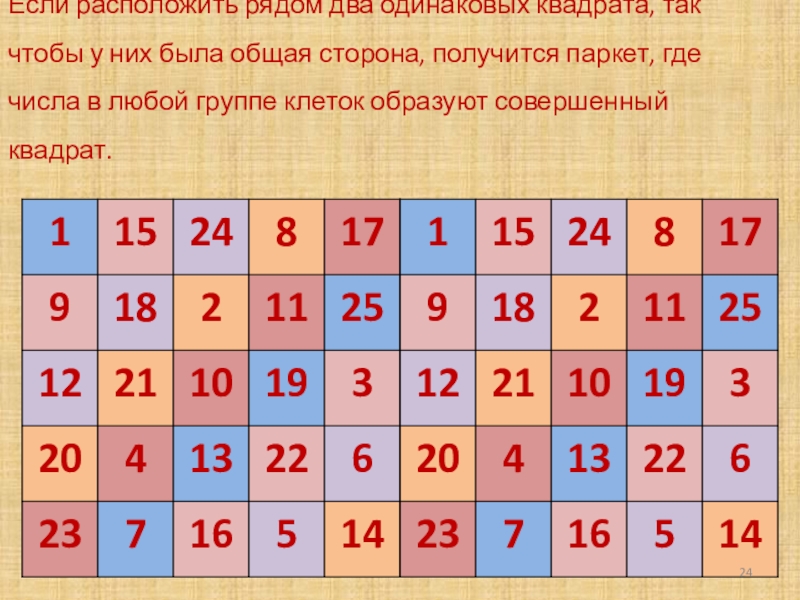
- 24. Если расположить рядом два одинаковых квадрата,
- 25. Рассмотрим свойства магического квадрата 5х5, имеющий в
- 26. Симметричность квадратов- что это такое?Квадрат, в котором
- 27. Как построить магический квадрат нечетного порядка (
- 28. Несложно составить магический квадрат 4х4: запишем все
- 29. Метод террас (метод Баше) С четырёх
- 30. Магический квадрат Пифагора. С помощью магического квадрата
- 31. Великий ученый Пифагор считал, что сущность человека
- 32. Ячейка 1 – целеустремленность, воля, упорство, эгоизм.1
- 33. Ячейка 2 – биоэнергетика, эмоциональность, душевность, чувственность.
- 34. Ячейка 3 – точность, конкретность, организованность, аккуратность,
- 35. Ячейка 5 – интуиция, ясновидение,
- 36. Ячейка 6 – заземленность, материальность, расчет, склонность
- 37. Восьмерок нет – у этих людей почти
- 38. «В дни моей юности я в свободное
- 39. Так же очень популярна японская головоломка судоку,
- 40. Выводы:В проекте рассмотрена история возникновения одного из
- 41. ЗаключениеМатематики всегда опережали время, в котором живут.
Слайд 1 Магические квадраты
Слайд 2«Далёкое время Застыло на камне, А мы прикоснулись к нему. Попала к нам в
Слайд 3”Я не знаю ничего более прекрасного в арифметике, чем эти числа, называемые
Пьер де Ферма
Слайд 8Гипотеза:
Изучение свойств магических квадратов даст возможность любому построить этот квадрат.
Слайд 9Цели и задачи моей работы:
изучить историю возникновения магических квадратов;
выяснить способы
научиться строить магические квадраты разного порядка разными способами;
опробовать найденные способы заполнения магических квадратов;
выяснить возможность применения магических квадратов в деятельности человека, а так же в науке.
Слайд 10Из истории развития магических квадратов
Магические квадраты возникли в глубокой древности в Китае.
Слайд 13Магический квадрат-
это квадрат, сумма чисел которого
в каждом
в каждом вертикальном ряду и
по каждой из диагоналей
одна и та же.
Слайд 14Магический квадрат 2х2
Магических квадратов 2х2 не существует.
Квадрат размером 2x2:
два столбца и
две диагонали,
он должен был бы состоять из чисел 1, 2, 3,4
(1+2+3+4):2=5
Число 5 нужно представить в виде суммы двух данных
чисел шестью различными способами,
но это сделать невозможно: 5=1+4=2+3
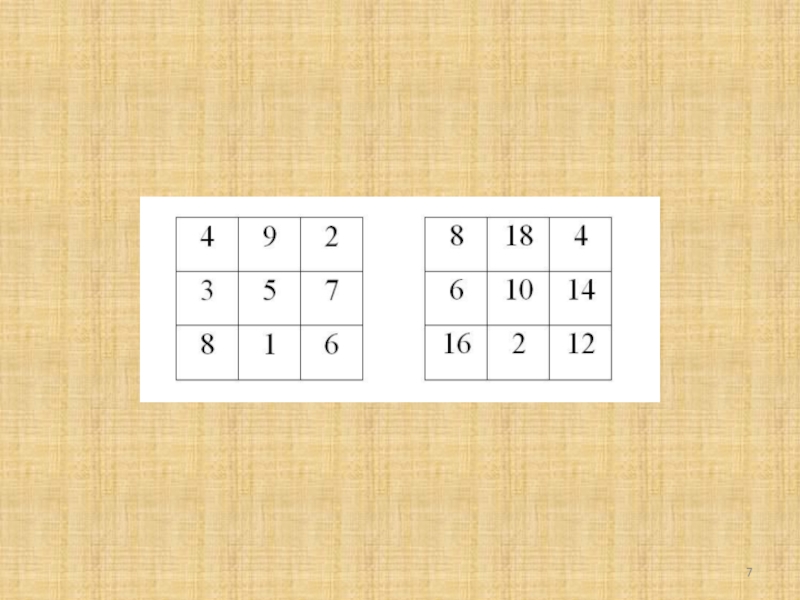
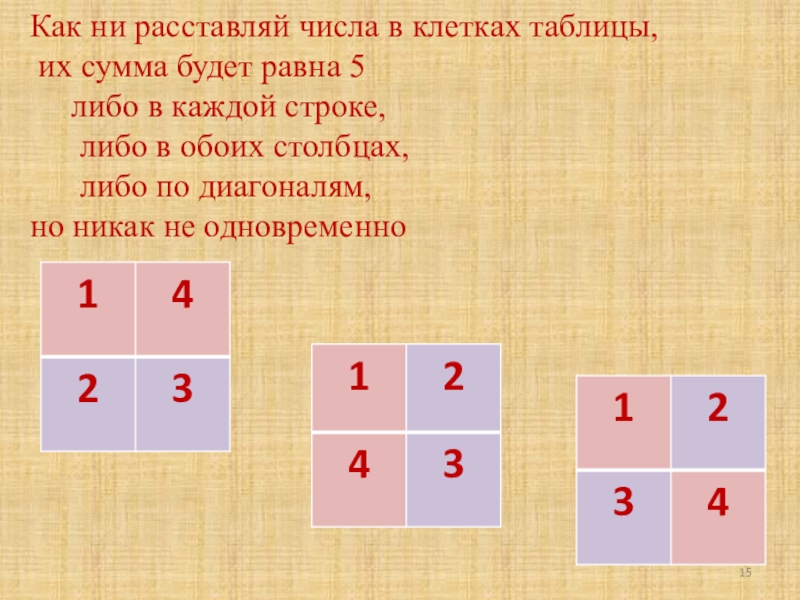
Слайд 15Как ни расставляй числа в клетках таблицы, их сумма будет равна
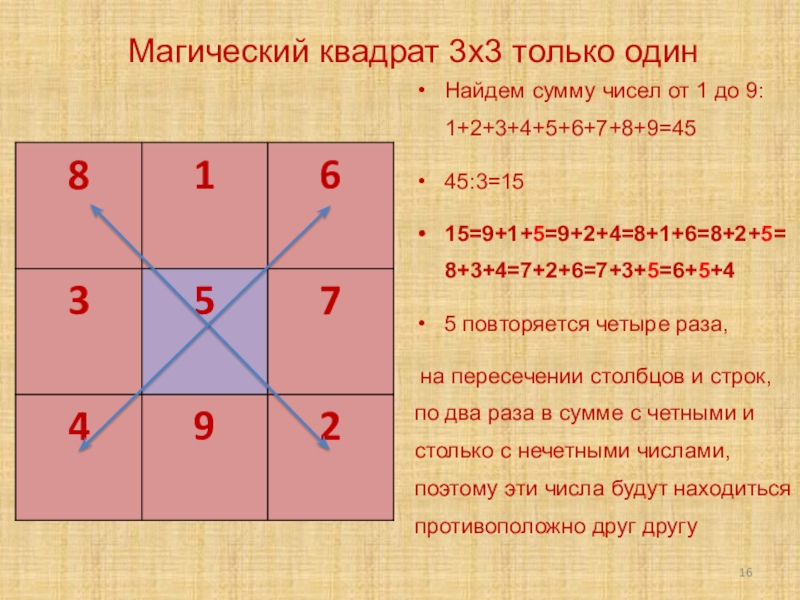
Слайд 16Магический квадрат 3х3 только один
Найдем сумму чисел от 1 до 9:
45:3=15
15=9+1+5=9+2+4=8+1+6=8+2+5=8+3+4=7+2+6=7+3+5=6+5+4
5 повторяется четыре раза,
на пересечении столбцов и строк, по два раза в сумме с четными и столько с нечетными числами, поэтому эти числа будут находиться противоположно друг другу
Слайд 171.Из магического квадрата можно получить новый, с увеличением всех чисел квадрата
Слайд 182. Все остальные магические квадраты 3 х3 получаются из него либо
Слайд 19 В магическом квадрате 4х4 сумма чисел по каждой строке, каждому
Слайд 20Сумма цифр в каждом квадрате 2х2 равна 34; в каждом столбце
Слайд 21 Это знаменитый магический квадрат Дюрера. Он изображен на гравюре великого немецкого
Слайд 22Магический квадрат 5х5
Суммы пятерок чисел на разломанных диагоналях равны постоянному числу
(1+2+3+4+…22+23+24+25):5.Такие квадраты называются совершенными.
Мы уже знаем, что квадрат останется совершенным, если подвергнуть его таким преобразованиям, как поворот и симметрия.
Слайд 23Квадрат останется совершенным, после того как его верхнюю строку заменят нижней
Слайд 24 Если расположить рядом два одинаковых квадрата, так чтобы у них была
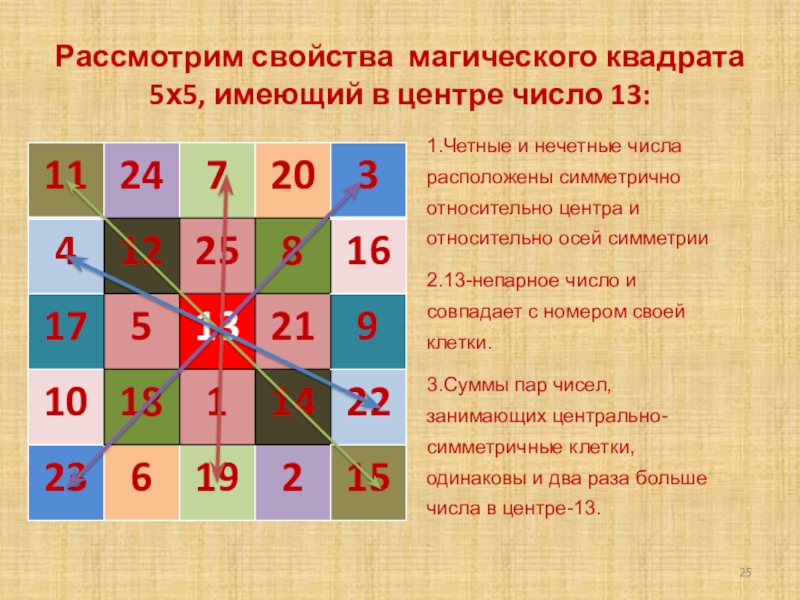
Слайд 25Рассмотрим свойства магического квадрата 5х5, имеющий в центре число 13:
1.Четные
2.13-непарное число и совпадает с номером своей клетки.
3.Суммы пар чисел, занимающих центрально-симметричные клетки, одинаковы и два раза больше числа в центре-13.
.
Слайд 26Симметричность квадратов- что это такое?
Квадрат, в котором любые два числа, расположенные
Слайд 27Как построить магический квадрат нечетного порядка ( метод французского геометра 17
В первой клетке среднего столбца пишем число 1. Ниже нижней клетки тоже пишем 1 и от него идя вверх и вправо числа 2 и3.
Когда дойдем до самого правого столбца это число 3 записываем слева от квадрат и пишем вправо вверх числа в порядке возрастания.
Доходим до 1 и опускаемся ниже на одну клетку вниз, записываем в ней следующее число и снова пишем числа в порядке возрастания по диагонали.
После чего процесс заполнения продолжается..
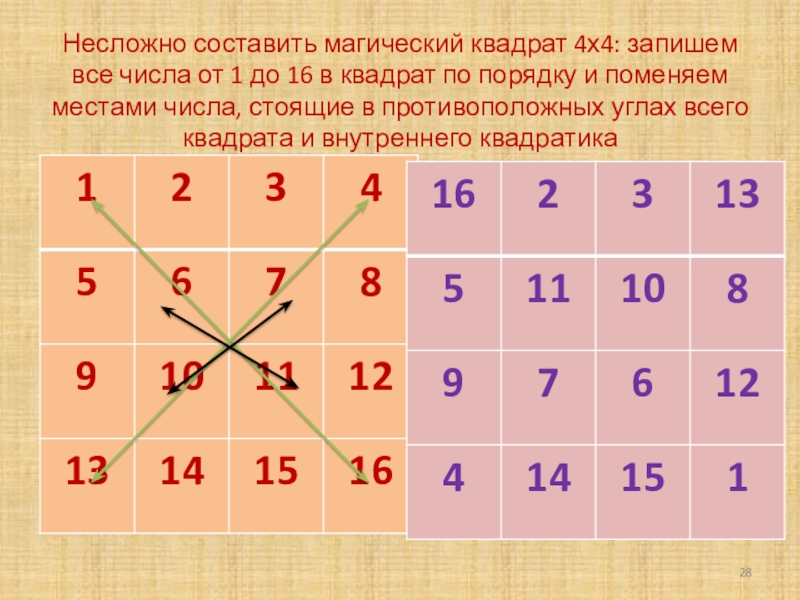
Слайд 28Несложно составить магический квадрат 4х4: запишем все числа от 1 до
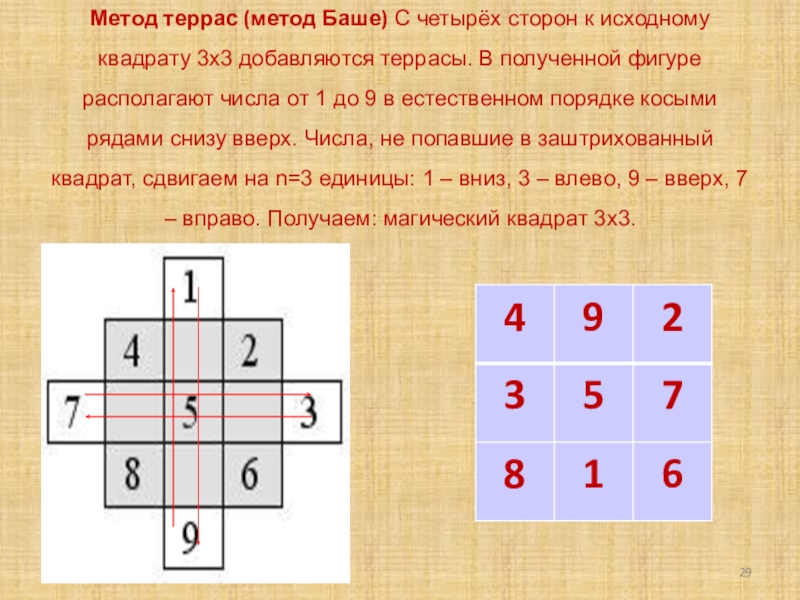
Слайд 29 Метод террас (метод Баше) С четырёх сторон к исходному квадрату 3х3
Слайд 30Магический квадрат Пифагора.
С помощью магического квадрата Пифагора можно познать характер человека,
Слайд 31Великий ученый Пифагор считал, что сущность человека заключается тоже в числе
24.04.2004г.- дата моего рождения.
Сложим цифры дня, месяца и года рождения (без нулей): 2+4+4+2+4=16.
Складываем цифры результата: 1+6=7. Затем из первой суммы вычитаем удвоенную первую цифру дня рождения: 16-4=12. И вновь складываем цифры последнего числа: 1+2=3. Получили числа 24.04.2004,16,7,12,3 составляем магический квадрат так, чтобы все единицы этих чисел вошли в ячейку 1, все двойки – в ячейку 2
и т.д. Нули при этом во внимание не принимаются. В результате квадрат будет выглядеть следующим образом.
Слайд 32Ячейка 1 – целеустремленность, воля, упорство, эгоизм.
1 – законченные эгоисты, стремятся
11 – характер, близкий к эгоистическому.
111 – «золотая середина», Характер спокойный, покладистый, коммуникабельный.
1111 – люди сильного характера, волевые. Мужчины с таким характером подходят на роль военных – профессионалов, а женщины держат семью в кулаке.
11111 – диктатор, самодур.
111111 – человек жестокий, способный совершить невозможное; нередко попадает под влияние какой-то идеи.
Слайд 33Ячейка 2 – биоэнергетика, эмоциональность, душевность, чувственность. Количество ячеек определяет уровень
Двоек нет – открыт канал для интенсивного набора биоэнергетики. Эти люди воспитаны и благородны от природы.
2 – обычные в биоэнергетическом отношении люди. Такие люди очень чувствительны к изменениям в атмосфере.
22 – относительно большой запас биоэнергетики. Из таких людей получаются хорошие врачи, медсестры, санитары. В семье таких людей редко у кого бывают нервные стрессы.
222 – знак экстрасенса.
Слайд 34Ячейка 3 – точность, конкретность, организованность, аккуратность, пунктуальность, чистоплотность, скупость, наклонность
Нарастание троек усиливает эти качества. С ними человеку есть смысл искать себя в науках, особенно точных. Перевес троек порождает педантов, людей в футляре.
Ячейка 4 – здоровье. Это связано с энергетическим пространством, наработанным предками и защищающим человека. Отсутствие четверок свидетельствует о болезненности человека.
4 – здоровье среднее, необходимо закалять организм. Из видов спорта рекомендуется плавание и бег.
44 – здоровье крепкое.
444 и более – люди с очень крепким здоровьем.
Слайд 35 Ячейка 5 – интуиция, ясновидение, начинающее проявляться у таких
Пятерок нет – канал связи с космосом закрыт. Эти люди часто ошибаются.
5 – канал связи открыт. Эти люди могут правильно рассчитать ситуацию, извлечь из нее максимальную пользу.
55 – сильно развита интуиция. Когда видят «вещие сны», могут предугадывать ход событий. Подходящие для них профессии – юрист, следователь.
555 – почти ясновидящие.
5555 – ясновидящие.
.
Ячейка 7 – количество семерок определяет меру таланта.
7 – чем больше они работают, тем больше получают впоследствии.
77 – очень одаренные, музыкальные люди, обладают тонким художественным вкусом, могут иметь склонность к изобразительному искусству.
777 – эти люди, как правило, приходят на землю ненадолго. Они добры, безмятежны, болезненно воспринимают любую несправедливость. Они чувствительны, любят мечтать, не всегда чувствуют реальность.
7777 – знак Ангела. Люди с таким знаком умирают в младенчестве, а если и живут, то их жизни постоянно угрожает опасность.
Слайд 36Ячейка 6 – заземленность, материальность, расчет, склонность к количественному освоению мира
Шестерок нет – этим людям необходим физический труд, хотя они его, как правило, не любят. Они наделены неординарным воображением, фантазией, художественным вкусом. Тонкие натуры, они тем не менее способны на поступок.
6 – могут заниматься творчеством или точными науками, но физический труд является обязательным условием существования.
66 – люди очень заземлены, тянуться к физическому труду, хотя как раз для них он не обязателен; желательна умственная деятельность, либо занятия искусством.
666 – знак Сатаны, особый и зловещий знак. Эти люди обладают повышенным темпераментом, обаятельны, неизменно становятся в обществе центром внимания.
6666 – эти люди в своих предыдущих воплощениях набрали слишком много заземленности, они очень много трудились и не представляют свою жизнь без труда. Если в их квадрате есть девятки, им обязательно нужно заниматься умственной деятельностью, развивать интеллект, хотя бы получить высшее образование.
Слайд 37Восьмерок нет – у этих людей почти полностью отсутствует чувство долга.
8
88 – у этих людей развито чувство долга, их всегда отличает желание помочь другим, особенно слабым, больным, одиноким.
888 – знак великого долга, знак служения народу. Правитель с тремя восьмерками добивается выдающихся результатов.
8888 – эти люди обладают парапсихологическими способностями и исключительной восприимчивостью к точным наукам.
Ячейка 9 – ум, мудрость.
Отсутствие девяток – свидетельство того, что умственные способности крайне ограничены.
9 – эти люди должны всю жизнь упорно трудиться, чтобы восполнить недостаток ума.
99 – эти люди умны от рождения. Учатся всегда неохотно, потому что знания даются им легко. Они наделены чувством юмора с ироничным оттенком, независимые.
999 – очень умны. К учению вообще не прикладывают никаких усилий. Прекрасные собеседники.
9999 – этим людям открывается истина. Если у них к тому же развита интуиция, то они гарантированы от провала в любом из своих начинаний.
Слайд 38«В дни моей юности я в свободное время развлекался тем, что
В 16-17 вв. составлением магических квадратов занимались с таким же увлечением, с каким сегодня составляют кроссворды, даже такие математики, как Клод Гаспар Баше, Паскаль Блез, Михаэль Штифель
Паскаль Ферма, Гаусс Карл Фридрих.
Именно в одной из книг Баше магические квадраты предстали, как математическая забава.
Слайд 39Так же очень популярна японская головоломка судоку, прародителем которой можно считать
Слайд 40Выводы:
В проекте рассмотрена история возникновения одного из интересных вопросов математики -
Сегодня таинственностью незатейливых суммирующих закономерностей уже никого не удивишь. Человек научился строить магические квадраты самого разного порядка.
Магические квадраты могут рассматриваться не только в качестве задач из математических курьезов, сегодня уже известно об их применение в новейших цифровых технологиях, в программировании.
.