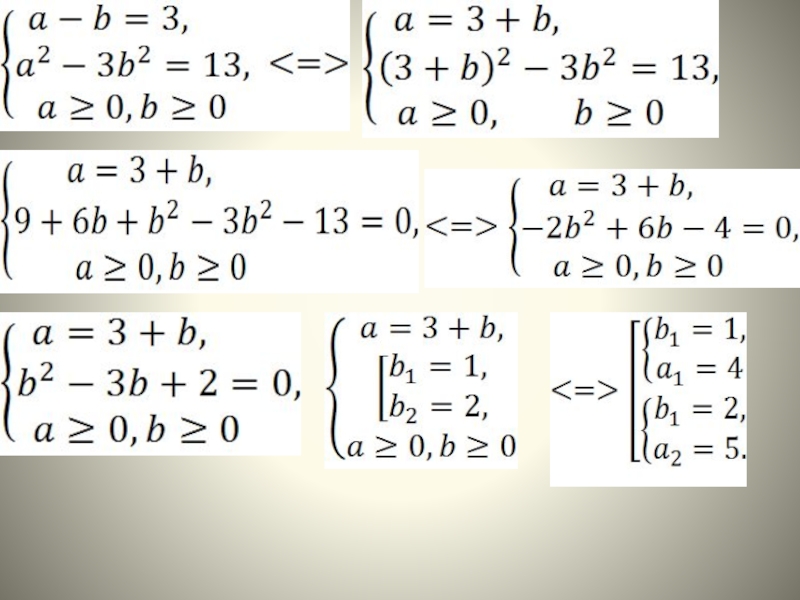- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к исследовательской работе
Содержание
- 1. Презентация к исследовательской работе
- 2. «Мне приходится делить время между
- 3. Слайд 3
- 4. Способ 1. Метод пристального взгляда (устно).Ответ: 5, 8.
- 5. Вывод: Решая уравнение методом пристального взгляда не
- 6. Способ 2. Метод возведения обеих частей уравнения
- 7. перенесем правую часть уравнения влево и приведем
- 8. Вывод: При решении уравнений данным методом необходимо вести
- 9. Способ 3. Метод равносильных преобразований
- 10. По теореме Виета:Ответ: 5; 8
- 11. Вывод: При решении уравнений данным методом нужно четко
- 12. Способ 4. Функционально графический метод Рассмотрим функции
- 13. Cоставим таблицу значений.
- 14. Вывод: функционально графический метод – это наглядный
- 15. Способ 5. Метод введения новых переменных. Введем новые
- 16. Слайд 16
- 17. По теореме Виета:Вернемся к переменной х:1) .Ответ: 5;8.
- 18. Вывод: Метод введения новых переменных и переход к
- 19. Способ 6. Метод умножения обеих частей уравнение на
- 20. Оба этих числа входят в область определения исходного уравнения, значит, являются корнями.Ответ: 5,8.
- 21. Вывод: При решении уравнения данным методом нужно
- 22. Заключение: Решение одной и той же задачи
- 23. спасибоЗа внимание!
Слайд 2
«Мне приходится делить время
между политикой и уравнениями.
Однако, уравнения, по-моему,
Политика существует для данного момента,
а уравнения будут существовать вечно».
Эйнштейн
Цель: Рассмотреть несколько методов решения одного иррационального уравнения.
Задачи: Показать, что иррациональные уравнения можно решить различными способами.
Слайд 5
Вывод: Решая уравнение методом пристального взгляда не нужно вести запись, отсутствует
Слайд 6Способ 2. Метод возведения обеих частей уравнения в одну и ту
возведем обе части уравнения в квадрат:
приведем подобные слагаемые:
разделим обе части уравнения на 2:
возведем обе части уравнения в квадрат:
Слайд 7перенесем правую часть уравнения влево и приведем подобные слагаемые:
Значит,
2)
Проверка: 1)
Значит, число 8 является корнем уравнения.
Уравнение имеет два решения 5 и 8.
Ответ: 5, 8.
Слайд 8Вывод: При решении уравнений данным методом необходимо вести словесную запись, что делает
Слайд 11Вывод: При решении уравнений данным методом нужно четко знать, когда ставить знак
Слайд 12Способ 4. Функционально графический метод
Рассмотрим функции
1)
и
- степенная функция. Найдем область определения функции
(f).
.
2)
– степенная функция.
.
Слайд 14
Вывод: функционально графический метод – это наглядный метод, но применять его
Слайд 15Способ 5. Метод введения новых переменных.
Введем новые переменные, обозначив
Получим первое
Составим второе уравнение системы:
Получим систему двух рациональных уравнений, относительно а и b:
Слайд 18Вывод: Метод введения новых переменных и переход к системе рациональных уравнений для
Слайд 19Способ 6. Метод умножения обеих частей уравнение на выражение сопряженное данному .
Рассмотрим это же уравнение:
Найдем область определения исходного уравнения:
Заметим, что
Домножим левую и правую часть уравнения на выражение
Слайд 20 Оба этих числа входят в область определения исходного уравнения, значит,
Ответ: 5,8.