- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к факультативному занятию по математике на тему Делимость чисел
Содержание
- 1. Презентация к факультативному занятию по математике на тему Делимость чисел
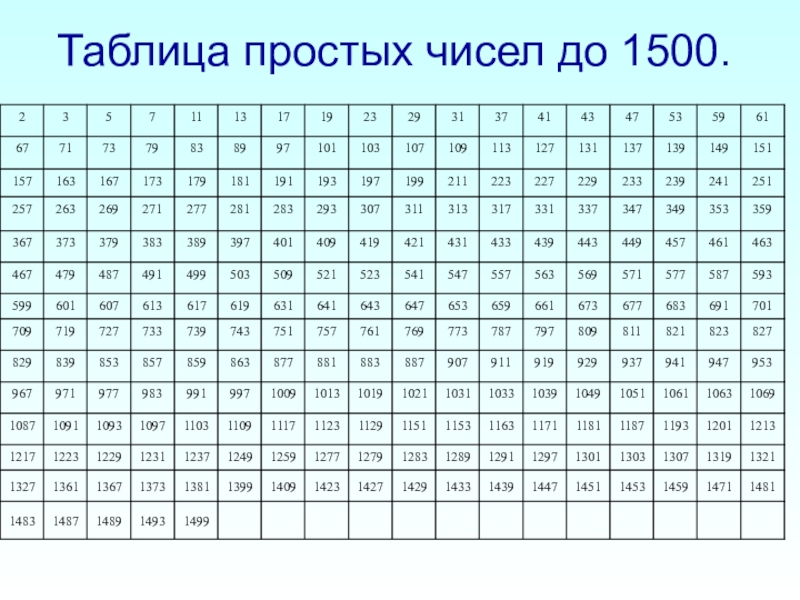
- 2. Таблица простых чисел до 1500.
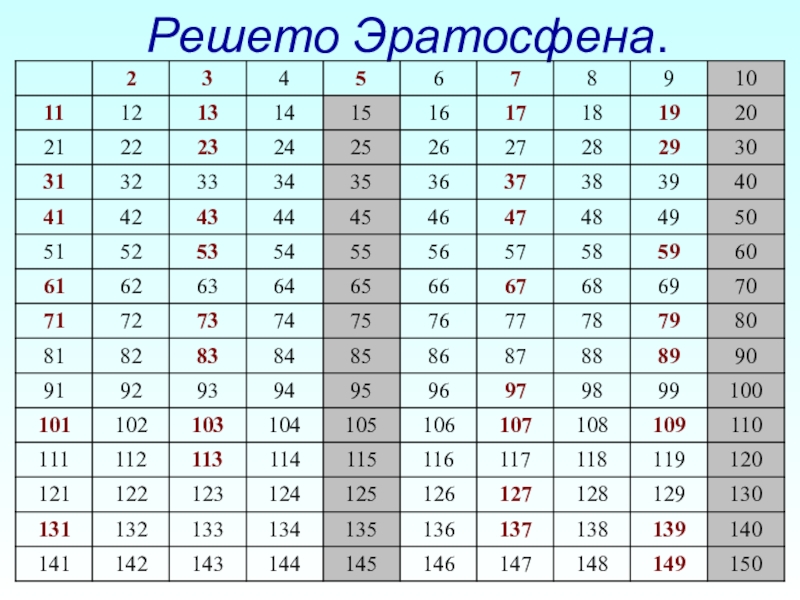
- 3. Решето Эратосфена.
- 4. Если простые числа отличаются на 2, то
- 5. Марен Мерсенн (1588 - 1648) - французский
- 6. Задание 2. Найдите первых шесть чисел Мерсена
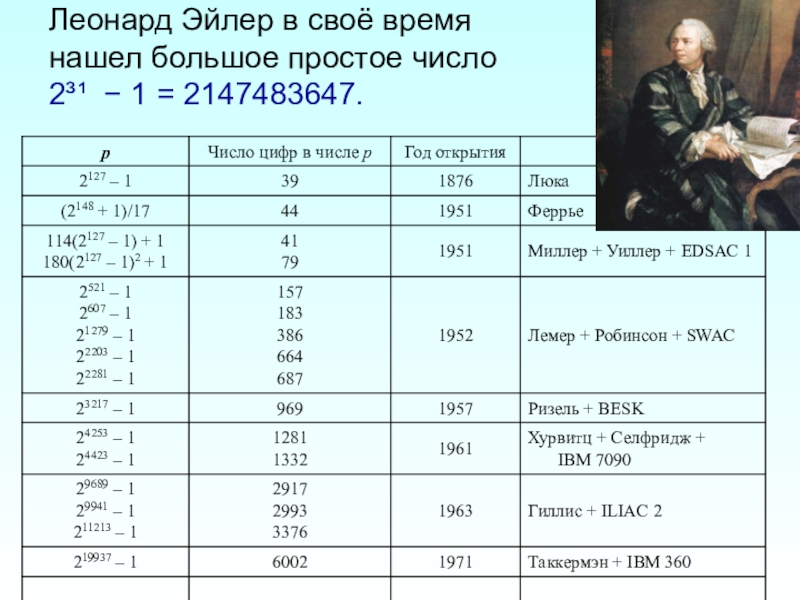
- 7. Леонард Эйлер в своё время нашел
- 8. Число называется совершенным, если оно равно сумме
- 9. Задание 3. Найдите три совершенных числа. Решение.Если
- 10. Любое целое число можно представить в виде
- 11. Признаки делимости по ним можно определить, делится
- 12. Признаки делимости на составные числа. Число делится
- 13. если число делится на два взаимно простых
- 14. Свойства делимости Если каждое из слагаемых делится
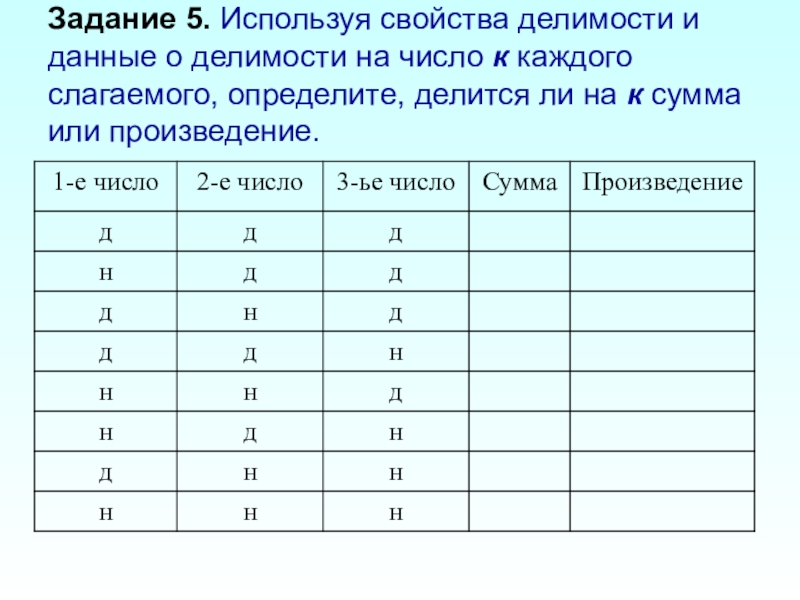
- 15. Задание 5. Используя свойства делимости и данные
- 16. Слайд 16
- 17. Задание 7. Укажите, какие из следующих утверждений
- 18. Общие делители и кратные. Общим делителем нескольких чисел
- 19. Например, числа 18, 12, 6, 120, 60
- 20. Рассмотрим множество делителей числа 20 и множество
- 21. Задание 9. Найдите НОД и НОК для
- 22. Существует способ для вычисления НОД двух чисел
- 23. Задание 10. Вася рвёт газету на 8
- 24. Задание 13. На какую цифру оканчивается число
- 25. Свойства остатков. n=km + r, где 0≤ r
- 26. Слайд 26
- 27. Основные свойства остатков:Пусть остаток от деления целого
- 28. Задание 19. Не используя калькулятор и вычисления
- 29. Задание 20 (Кенгуру-1998). Каков остаток от деления
Слайд 4Если простые числа отличаются на 2, то их называют числами-близнецами.
Ответ:
Например, в первой сотне это 3 и 5, 5 и 7, 11 и 13, 17 и 19,
29 и 31, 41 и 43, 59 и 61, 71 и 73.
Назовите числа-близнецы из пятой сотни.
Слайд 5Марен Мерсенн (1588 - 1648) - французский математик и философ.
Мр
М2 = 22- 1 = 3; простое число;
М3= 23- 1 = 7; простое число;
Слайд 6Задание 2. Найдите первых шесть чисел Мерсена и определите, есть ли
Решение.
М5 = 25- 1 = 31; простое число.
М7 = 127 - простое число.
М11 = 2047 – составное (23∙89).
М13 =8191 –простое.
Ответ: М11 – составное число.
Слайд 8Число называется совершенным, если оно равно сумме своих делителей, отличных от
6 – совершенное число, так как 6 = 1 + 2 + 3.
Найдите ещё несколько совершенных чисел
Просто ли это сделать?
В чём трудность?
Слайд 9Задание 3. Найдите три совершенных числа.
Решение.
Если р = 3, 2р-
2p–1(2p – 1) = 23–1(23 – 1) = 4∙7 = 28. 28 = 1 + 2 + 4 + 7 + 14.
Если р = 5, 2р- 1 = 25- 1 = 31,
2p–1(2p – 1) = 25–1(25 – 1) =16∙31 =496.
496 = 1 + 2 + 4 + 6 + 16 + 31 + 62 + 124 + 248.
Если р = 7, 2р- 1 = 27- 1 = 127,
2p–1(2p – 1) = 27–1(27– 1) =64∙127 =8128.
8128 = 1 + 2 + 4 +8 + 16 + 32+ 64 + 127 + 254 + 508 +1016 + 2032 + 4064.
Ответ: 28, 496, 8128.
Слайд 10Любое целое число можно представить в виде произведения простых чисел или
504 = 2×2×2×3×3×7
504 = 3×2×7×3×2×2 = 7×3×2×2×3×2
Основная теорема арифметики.
Любое натуральное число, отличное от единицы, раскладывается на произведение простых чисел единственным образом.
Запись числа в виде произведения степеней в порядке возрастания их оснований называется каноническим разложением числа:
504 = 23×32×71
Слайд 11Признаки делимости
по ним можно определить, делится ли натуральное число n
Число делится на 2, если оно оканчивается на 0, 2, 4, 6 или 8, то есть если оно чётное.
Число делится на 5, если оно оканчивается на 0 или 5.
Число делится на 3 или на 9, если сумма цифр числа делится на 3 или на 9 соответственно.
Число делится на 11, если разность суммы цифр, стоящих на чётных местах, и суммы цифр, стоящих на нечётных местах, делится на 11.
Например, число 1969 делится на 11, т.к. сумма цифр, стоящих на чётных местах, равна 18, а на нечётных - 7.
Число делится на 7 или на 13, если на эти числа делится разность числа тысяч и числа, выражаемого последними тремя цифрами; эта операция уменьшает число знаков в числе, и последовательное её применение приводит к трёхзначному числу.
Например, 825678 делится на 7, т.к. 825-678 = 147 делится на 7.
Слайд 12Признаки делимости на составные числа.
Число делится на 4, если число,
Число делится на 8, если число, записываемое тремя последними цифрами этого числа, делится на 8.
Слайд 13если число делится на два взаимно простых числа, то оно делится
на 6 = 2×3, на 12 = 3×4, на 15 = 3×5, на 18 = 2×9 и т.д.
На 6 делятся те и только те числа, которые делятся и на 2 и на 3.
Например, 12432 делится на 6, так как делится и на 2 и на 3.
На 12 делятся те и только те числа, которые делятся и на 3 и на 4 (но не 2 и на 6, так как 2 и 6 имеют общий множитель).
Например, 75348 делится на 12, так как делится и на 3 и на 4.
На 15 делятся те и только те числа, которые делятся и на 3 и на 5.
Например, 23520 делится на 15, так как делится и на 3 и на 5.
На 18 делятся те и только те числа, которые делятся и на 2 и на 9.
Например, 13518 делится на 18, так как делится и на 2 и на 9, и т.д.
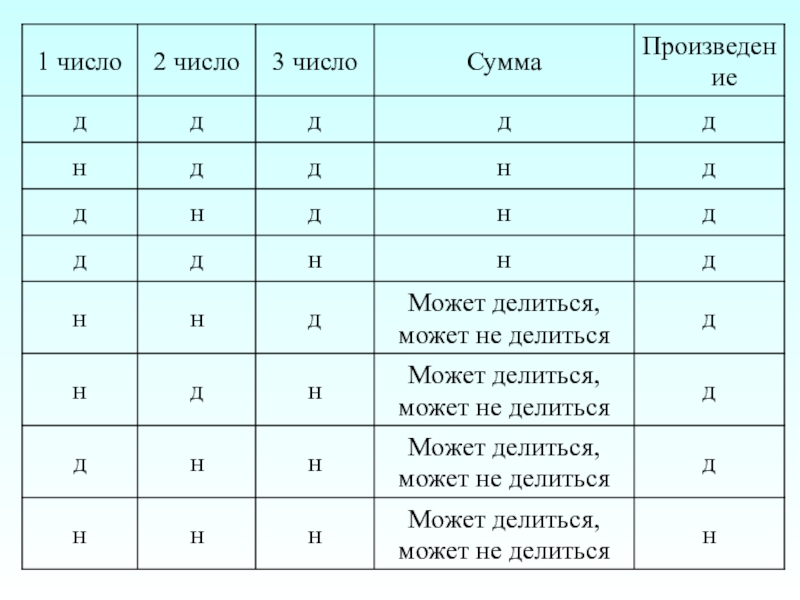
Слайд 14Свойства делимости
Если каждое из слагаемых делится на какое-то число, то
Если каждое слагаемое, кроме одного, делится на какое-нибудь число, а одно не делится, то сумма не делится на это число.
Если уменьшаемое и вычитаемое делится на какое-нибудь число, то и разность разделится на это число.
Если только одно из чисел – уменьшаемое или вычитаемое - делится на какое-нибудь число, а другое не делится, то и разность не делится на это число.
Если хоть один из сомножителей делится на какое-нибудь число, то и произведение их также разделится на это число.
Слайд 15Задание 5. Используя свойства делимости и данные о делимости на число
Слайд 17Задание 7. Укажите, какие из следующих утверждений ложные.
А) Если слагаемые не
Ложное. Пример: 7+3 = 10; 7 и 3 не делятся на 5, а 10 делится на 5.
Б) Если произведение двух чисел делится на какое-либо число, то хотя бы один из множителей делится на это число.
Ложное. Пример: 6 ⋅ 10 = 60; 60 делится на 15, а ни 6, ни 10 не делятся
В) Если множители не делятся на какое-нибудь число, то и произведение не делится на это число.
Ложное. Пример: 6 ⋅ 10 = 60; ни 6, ни 10 не делятся на 15, а 60 делится на 15.
Г) Если разность делится на какое-нибудь число, то и уменьшаемое, и вычитаемое делится на это число.
Ложное. Пример: 23 - 21 = 2. Разность 2 делится на 2, а 23 и 21 на 2 не делятся.
Слайд 18Общие делители и кратные.
Общим делителем нескольких чисел называется число, на которое
НОД (48, 36, 24)=
Взаимно простые числа –
Числа у которых наибольший общий делитель равен единице.
Например, НОД (16, 27) =1
Слайд 19Например, числа 18, 12, 6, 120, 60 являются общими кратными для
Наименьшим общим кратным нескольких чисел называется наименьшее натуральное число, которое делится на каждое из данных чисел.
Например, 6 – наименьшее общее кратное для 2 и 3.
Общим кратным данных чисел называется любое натуральное число, которое делится на каждое из данных чисел (без остатка).
Слайд 20Рассмотрим множество делителей числа 20 и множество делителей числа 30:
Д(20) =
Д(30) = {1, 2, 3, 5, 6, 10, 15, 30}.
Найдем объединение и пересечение этих множеств.
Д(20) ∪ Д(30) = {1, 2, 3, 4, 5, 6, 10, 15, 20, 30}
Д(20) ∩ Д(30) = {1, 2, 5, 10}.
НОД (20,30) = 10,
НОД нескольких чисел – это наибольший элемент из пересечения множеств делителей этих чисел.
Слайд 21Задание 9. Найдите НОД и НОК для чисел: А) 18, 63; Б)
Ответ:
А) НОД(18,63) = 9; НОК(18,63) = 126.
Б) НОД(18,84) = 6; НОК(18,84) =252.
В) НОД(63,84) = 21; НОК(63,84) =252.
Г) НОД(18,63,84) = 3; НОК(18,63,84) = 252.
Слайд 22Существует способ для вычисления НОД двух чисел – алгоритм Евклида,
НОД(451-287,
НОД(164, 287) =
НОД(164, 123) =
НОД(41, 123) =
НОД (41, 82) =
НОД (41, 41) = 41.
Удобен, если числа большие.
1. Любой общий делитель чисел а и b (а > b) является делителем числа (а - b).
2. Любой общий делитель чисел b и (а - b) является делителем числа а.
НОД (а, b)= НОД (b, а - b)
НОД(451, 287) =
Слайд 23Задание 10. Вася рвёт газету на 8 частей, одну из получившихся
Решение.
В 1 раз - 8 частей,
во 2 раз - 15 разных частей (1∙7+8),
в 3 раз - 22 части (2⋅7+8) и т.д.,
каждый раз количество кусочков увеличивается на 7 частей,
общее количество частей всегда имеет вид К⋅7+8.
2013, его нельзя представить в виде К⋅7+8.
(2013 – 8 =2005, а 2005 не делится на 7).
Значит, Вася не сможет разорвать газету на 2013 частей.
Ответ: нет.
Слайд 24Задание 13. На какую цифру оканчивается число 3 ?
Решение.
Попробуем
3¹=3, 3²=9; 3³=27; 3 =81; 3 =243; 3 =729, 3 =2187 и т.д.
последние цифры степени числа 3 начинают повторяться в определенном порядке: 3, 9, 7, 1, 3, 9, 7, 1… и т. д.
повторяются всего 4 цифры (3, 9, 7, 1),
то есть число равное 3 , где n кратно четырём, всегда оканчивается на 1.
Разделим степень числа 3 на 4: 2013=4∙500 +13 = 4∙500 +12 + 1,
отсюда 32012 оканчивается на 1, а
3 оканчивается на 3.
Ответ: 3.
2013
4
5
6
7
п
2013
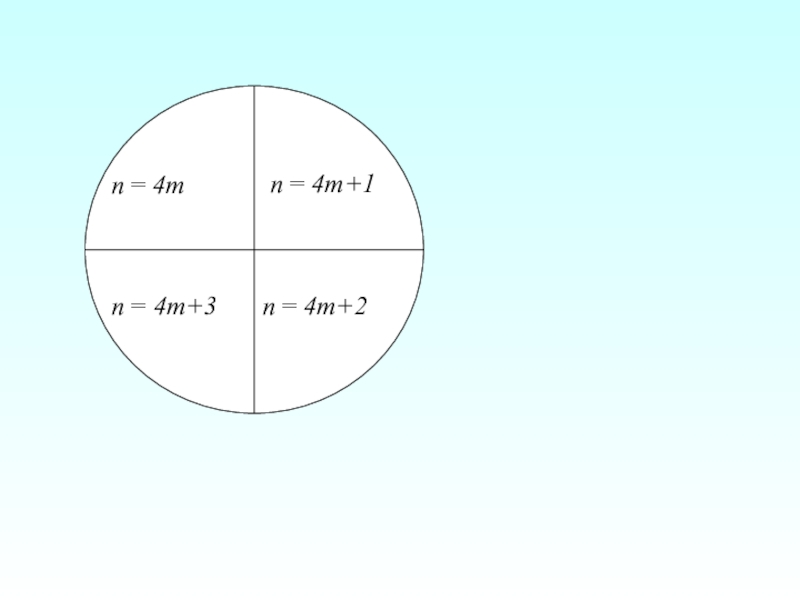
Слайд 25Свойства остатков.
n=km + r, где 0≤ r
k называется неполным частным от деления n на m, а r – остатком.
Задание 16. Запишите:
а) формулу чётного числа;
б) формулу нечётного числа;
в) формулу числа, кратного числу b;
г) формулу числа, которое делится на 17 с остатком 11.
n = 17m+11;
n = 2m+1;
n = bm
n = 2m
Слайд 27Основные свойства остатков:
Пусть остаток от деления целого числа n1 на m
Тогда:
Остаток от деления n1+n2 на m равен остатку от деления r1+r2 на m;
Остаток от деления n1–n2 на m равен остатку от деления r1–r2 на m;
Остаток от деления n1×n2 на m равен остатку от деления r1×r2 на m.
Слайд 28Задание 19. Не используя калькулятор и вычисления в столбик, найдите остаток
Решение.
Остаток от деления на 25 числа 53 равен 3, числа 55 равен 5, числа 27 - 2, числа 24 – 24, числа 101 - 1, числа 29 – 4.
Используя основные свойства остатков, получаем:
Остаток от деления на 25 произведения 53⋅55 равен 15 (3⋅5 =15, 15: 25 =0 (ост.15)).
Остаток от деления на 25 произведения 27⋅24 равен 23 (2⋅24 =48, 48:25= 1(ост.23)).
Остаток от деления на 25 произведения101⋅29 равен 4 (1⋅4=4, 4 : 25 = 0(ост.4)).
Тогда остаток от деления на 25 значения выражения 53⋅59 + 101⋅29 - 27⋅24 равен
остатку от деления на 25 числа 34 (15+23 – 4), то есть 9.
Ответ: 9.
Слайд 29Задание 20 (Кенгуру-1998). Каков остаток от деления 1997-значного числа 100…00 на
Решение.
Попробуем начать делить число 100…00 на 15.
Очевидно, что в результате деления остаток будет равен 10.
Ответ. 10.