Учитель математики МОУ «Осташевская СОШ»
Шорникова Светлана Павловна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад для внеурочного курса по математике 5 класс - Прямоугольник, квадрат, куб
Содержание
- 1. Презентация для внеурочного курса по математике 5 класс - Прямоугольник, квадрат, куб
- 2. Цель: Развитие пространственного воображения; Развитие логического мышления;Развитие тактильной памяти.
- 3. План урока: 1. Все вокруг -
- 4. I. Все вокруг - геометрия «Я думаю,
- 5. Геометрия зародилась в глубокой древности. Строя жилища
- 6. Почти все ученые древности и средних веков
- 7. II. Повторение пройденного материала Все фигуры, изображенные
- 8. Это интересно Градус в
- 9. III. Четырехугольники Фигуры, изображенные ниже, тоже
- 10. Как называется отрезок МК, изображенный на рисунке?
- 11. Это интересно Диагональ –
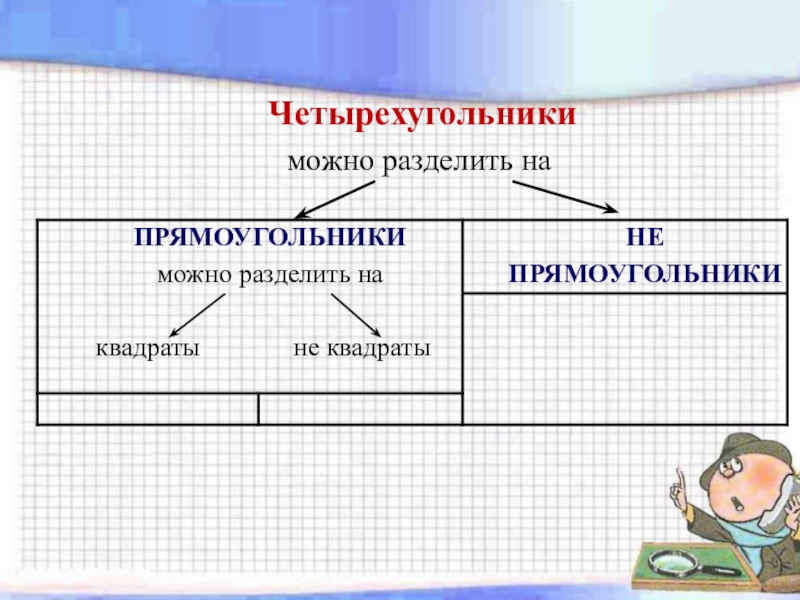
- 12. Четырехугольники можно разделить на
- 13. IV. Прямоугольник Прямоугольник – четырехугольник,
- 14. Исследуйте фигуру, которая находится у вас на
- 15. V. Квадрат Какая известная вам геометрическая фигураполучится, если у прямоугольника все стороныбудут равными?[Квадрат]
- 16. Квадрат – это четырехугольник, у которого все
- 17. Установим, какими свойствами обладает квадрат,
- 18. Самостоятельная работа Произведите классификацию предложенных четырехугольников
- 19. VI. Эксперимент. Центр тяжести квадрата Представьте себе,
- 20. Попробуем это проделать. Начертите диагонали картонного квадрата,
- 21. VI. Куб Геометрия изучает форму и взаимное
- 22. Представим себе, что перед нами дом и
- 23. Нам понадобилось задать три величины. Эти три
- 24. Но все же мы с вами живем
- 25. Развернем модели. Получим развертку куба. Поверхность куба
- 26. Поверхность каждого куба состоит из плоских многоугольников,
- 27. Правильный кубик Название «куб» произошло от греческого
- 28. Сколько у обычного кубика граней, вершин, ребер?Сколько
- 29. Спасибо за внимание
Цель: Развитие пространственного воображения; Развитие логического мышления;Развитие тактильной памяти.
Слайд 1Урок по математике для 5 класса
на тему:
«Прямоугольник, квадрат, куб»
Слайд 2
Цель:
Развитие пространственного воображения;
Развитие логического мышления;
Развитие тактильной памяти.
Слайд 3План урока:
1. Все вокруг - геометрия
2. Повторение пройденного материала
3. Четырехугольники
4. Прямоугольник
5. Квадрат
6. Эксперимент. Центр тяжести квадрата
7. Куб
3. Четырехугольники
4. Прямоугольник
5. Квадрат
6. Эксперимент. Центр тяжести квадрата
7. Куб
Слайд 4I. Все вокруг - геометрия
«Я думаю, что никогда, до настоящего
времени, мы не жили в такой геометрический период. Все вокруг – геометрия». Эти слова великого французского архитектора Ле Корбюзье (начало XX века) очень точно характеризуют и наше время.
Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Лучше ориентироваться в нем, открывать новое, понимать красоту и мудрость окружающего мира поможет вам эта наука.
Слайд 5 Геометрия зародилась в глубокой древности. Строя жилища и храмы, украшая их
орнаментами, размечая территории на поверхности земли, измеряя расстояния и площади земельных участков, человек применил свои знания о форме, размерах и взаимном расположении предметов, использовал свои геометрические знания, полученные из наблюдений и опытов.
Слайд 6 Почти все ученые древности и средних веков были выдающимися геометрами.
Один
из девизов древнегреческого философа Платона: «Не знающие геометрии не допускаются!» Было это приблизительно 2 400 лет назад.
Геометрия изучает форму
и взаимное расположение фигур.
Геометрия изучает форму
и взаимное расположение фигур.
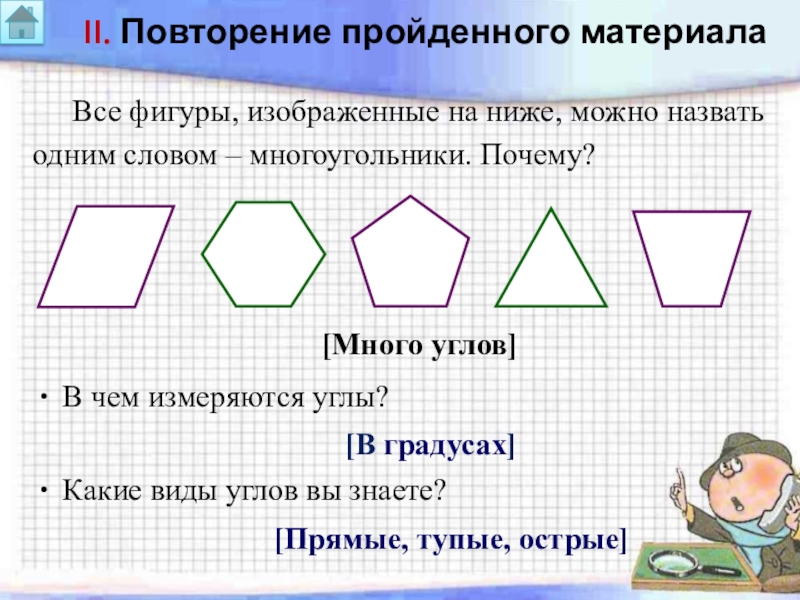
Слайд 7II. Повторение пройденного материала
Все фигуры, изображенные на ниже, можно назвать
одним словом – многоугольники. Почему?
[Много углов]
В чем измеряются углы?
[В градусах]
Какие виды углов вы знаете?
[Прямые, тупые, острые]
[Много углов]
В чем измеряются углы?
[В градусах]
Какие виды углов вы знаете?
[Прямые, тупые, острые]
Слайд 8Это интересно
Градус в переводе с латинского
– ступень, шаг. Температура тела повышается ... Стрелки часов идут …
Замените в слове «многоугольник» «много» на любое число. Получим название геометрической фигуры. Обратите внимание, у этих фигур, сколько сторон, столько и углов.
Замените в слове «многоугольник» «много» на любое число. Получим название геометрической фигуры. Обратите внимание, у этих фигур, сколько сторон, столько и углов.
Слайд 9III. Четырехугольники
Фигуры, изображенные ниже, тоже многоугольники.
Как их можно назвать
по-другому?
[Четырехугольники]
У этих многоугольников четыре угла и четыре стороны.
Вершины углов этого четырехугольника
называются вершинами четырехугольника.
Отрезки, соединяющие две соседние вершины,
называют сторонами четырехугольника.
[Четырехугольники]
У этих многоугольников четыре угла и четыре стороны.
Вершины углов этого четырехугольника
называются вершинами четырехугольника.
Отрезки, соединяющие две соседние вершины,
называют сторонами четырехугольника.
![III. Четырехугольники Фигуры, изображенные ниже, тоже многоугольники. Как их можно назвать по-другому? [Четырехугольники] У этих многоугольников](/img/thumbs/27f1d66e7c6eecde7970809b534dcdd2-800x.jpg "Презентация для внеурочного курса по математике 5 класс - Прямоугольник, квадрат, куб III. Четырехугольники Фигуры, изображенные ниже, тоже многоугольники. Как их можно назвать по-другому?")
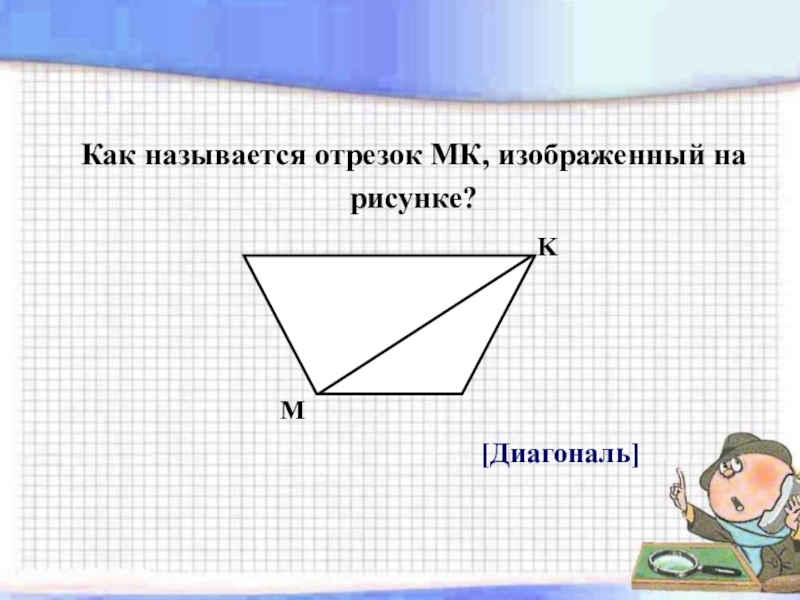
Слайд 11Это интересно
Диагональ – это отрезок, соединяющий две
не соседние вершины четырехугольника. Диагональ переводится как «идущая из угла в угол» или «идущая через угол».
Название каких четырехугольников вы знаете с раннего детства?
Какие многоугольники встречаются чаще всего в жизни?
Заполните таблицу
Слайд 13IV. Прямоугольник
Прямоугольник – четырехугольник, у которого все углы
прямые.
Является ли прямоугольником фигура, изображенная на рисунке?
[Нет]
Почему? Ведь у нее есть прямой угол.
[Необходимо, чтобы все
углы были прямыми]
Является ли прямоугольником фигура, изображенная на рисунке?
[Нет]
Почему? Ведь у нее есть прямой угол.
[Необходимо, чтобы все
углы были прямыми]
Найдите прямоугольники вокруг нас
Слайд 14 Исследуйте фигуру, которая находится у вас на столе. Установите, какими свойствами
она обладает, чем замечательна.
Свойства:
Противоположные стороны прямоугольника равны.
Диагонали прямоугольника равны.
Диагонали прямоугольника пересекаются
и точкой пересечения делятся пополам.
Свойства:
Противоположные стороны прямоугольника равны.
Диагонали прямоугольника равны.
Диагонали прямоугольника пересекаются
и точкой пересечения делятся пополам.
Задача
Слайд 15V. Квадрат
Какая известная вам геометрическая фигура
получится, если у прямоугольника все
стороны
будут равными?
[Квадрат]
будут равными?
[Квадрат]
![V. Квадрат Какая известная вам геометрическая фигураполучится, если у прямоугольника все стороныбудут равными?[Квадрат]](/img/tmb/5/467974/395cea3f3e55ddb95588675ce1775d5a-800x.jpg "Презентация для внеурочного курса по математике 5 класс - Прямоугольник, квадрат, куб V. Квадрат Какая известная вам геометрическая фигураполучится, если у прямоугольника все стороныбудут равными?[Квадрат]")
Слайд 16Квадрат – это четырехугольник, у которого все углы прямые и все
стороны равны.
Квадрат – это четырехугольник, у которого все углы прямые и все стороны равны.
Квадрат – это прямоугольник, у которого все стороны равны.
Квадрат – это четырехугольник, у которого все углы прямые и все стороны равны.
Квадрат – это прямоугольник, у которого все стороны равны.
Слайд 17Установим, какими свойствами обладает квадрат,
чем замечательна эта геометрическая фигура.
Диагонали квадрата равны.
Диагонали квадрата пересекаются и точкой пересечения делятся пополам.
«Разрезав» квадрат по диагоналям, получим равные треугольники.
Диагонали квадрата пересекаются под прямым углом.
Слайд 19VI. Эксперимент. Центр тяжести квадрата
Представьте себе, что острова любят путешествовать,
причем следующим образом: подлетает вертолет и поднимает остров за крючок, который расположен в определенном месте – точке пересечения диагоналей.
Слайд 20 Попробуем это проделать.
Начертите диагонали картонного квадрата, найдите точку их пересечения,
иголкой проколите в точке пересечения, поднимите на нитке. Остров в равновесии. От точности ваших построений зависит жизнь жителей острова: упадут в воду или нет.
Точка пересечения диагоналей прямоугольника является центром тяжести.
Точка пересечения диагоналей прямоугольника является центром тяжести.
Слайд 21VI. Куб
Геометрия изучает форму и взаимное расположение фигур в пространстве.
Это то пространство, которое окружает нас.
Слайд 22 Представим себе, что перед нами дом и мы хотим описать его,
то есть объяснить, какой он:
длина 2 подъезда;
ширина 2 окна;
высота 5 этажей.
длина 2 подъезда;
ширина 2 окна;
высота 5 этажей.
Слайд 23Нам понадобилось задать три величины.
Эти три измерения мы используем часто
(высота дерева, длина дороги, ширина тротуара).
Сколько измерений у прямоугольника?
[Два]
Слайд 24Но все же мы с вами живем в мире трех измерений,
в пространстве.
Пожалуй, трудно найти человека, которому бы не был знаком куб. Ведь «кубики» - это любимая игра малышей. Кажется, что мы о кубе знаем все, но так ли это?
Посмотрите на кубики. Дома попробуйте изготовить такие кубики сами.
Пожалуй, трудно найти человека, которому бы не был знаком куб. Ведь «кубики» - это любимая игра малышей. Кажется, что мы о кубе знаем все, но так ли это?
Посмотрите на кубики. Дома попробуйте изготовить такие кубики сами.
Слайд 25Развернем модели.
Получим развертку куба. Поверхность куба состоит из шести квадратов.
Куб иначе называют правильным гексаэдром («гекса» - шесть, «эдр» - грань).
Слайд 26Поверхность каждого куба состоит из плоских многоугольников, которые называются гранями.
Две соседние
грани многогранника имеют общую сторону, которая называется ребро.
Концы ребер сходятся в вершинах.
Концы ребер сходятся в вершинах.
Слайд 27Правильный кубик
Название «куб» произошло от греческого слова, означающего «игральная кость».
Секрет семерки: еще в древности люди преклонялись перед цифрой 7, считая, что она обладает магическими свойствами. Если нанести на кубик точки так, чтобы на противоположных гранях сумма очков была равна 7, то ваш кубик станет «магическим».
Слайд 28Сколько у обычного кубика граней, вершин, ребер?
Сколько всего очков на противоположных
гранях кубика?
Какова сумма очков на всех гранях кубика?
Сколько граней можно увидеть на кубике одновременно?
Какое максимальное число точек можно увидеть на игральном кубике?
Какое минимальное число точек можно
увидеть на игральном кубике?
Какова сумма очков на всех гранях кубика?
Сколько граней можно увидеть на кубике одновременно?
Какое максимальное число точек можно увидеть на игральном кубике?
Какое минимальное число точек можно
увидеть на игральном кубике?
