- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад для проведения Математической регаты (5 класс)
Содержание
- 1. Презентация для проведения Математической регаты (5 класс)
- 2. ПРИВЕТСТВУЕМ УЧАСТНИКОВ МАТЕМАТИЧЕСКОЙ РЕГАТЫ!
- 3. Да, путь познания не гладок.Но знайте вы
- 4. Регата - (итал. regata - от riga
- 5. Правила математической регаты1. Математическая регата – командное
- 6. I тур – разминка -
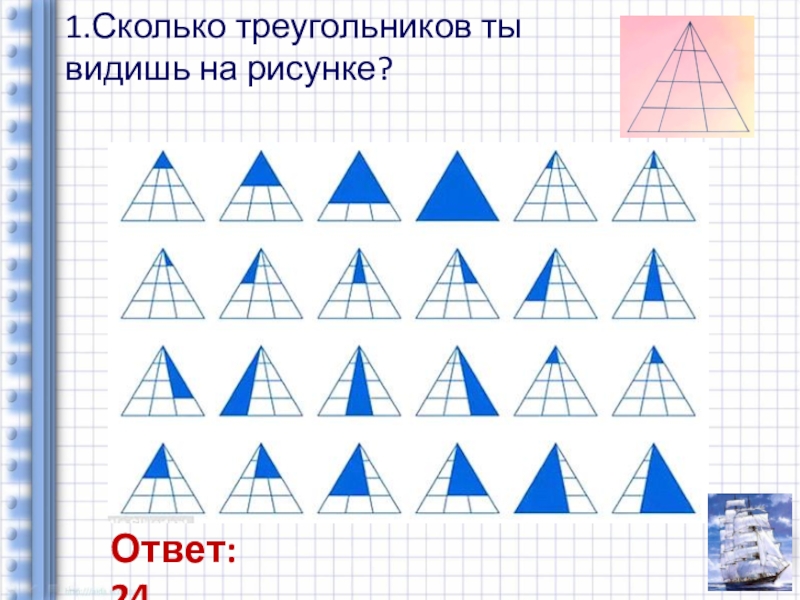
- 7. 1.Сколько треугольников ты видишь на рисунке?Ответ: 24
- 8. 2. Трехзначное число состоит из возрастающих
- 9. 3.Ваня раскладывает на столе камешки на расстоянии
- 10. 4. Какой цифрой заканчивается произведение всех нечётных
- 11. 5. Переместите одну спичку так, чтобы равенство стало верным.Ответ: Условие:
- 12. Подведём итоги!!!
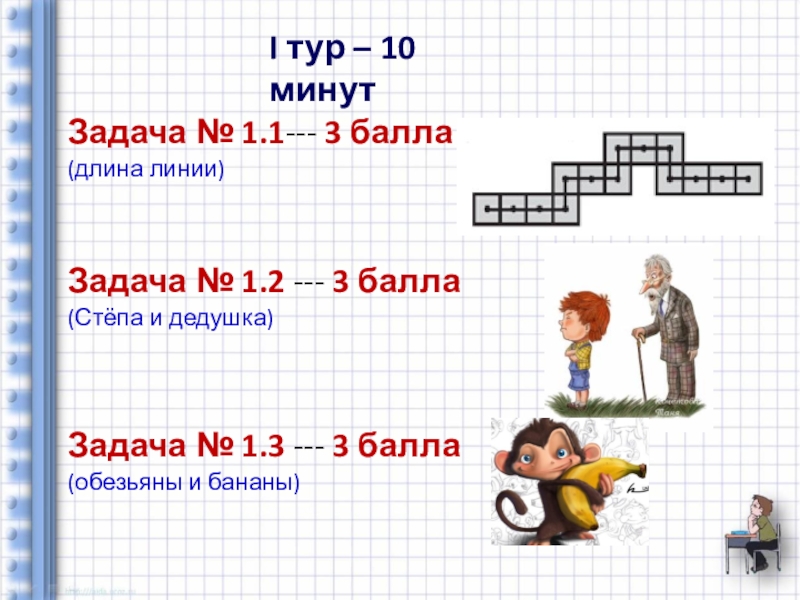
- 13. I тур – 10 минутЗадача № 1.1---
- 14. Задача 1.1 Дорожка выложена из 14
- 15. Задача 1.2 Степа учится в школе. Если
- 16. Нескольким обезьянам раздали 45 бананов так, что
- 17. Подведём итоги!!!
- 18. Задача № 2.1 --- 5 баллов (расставить
- 19. На рисунке изображена развертка кубика. На ней
- 20. Ваня стреляет в тире. Он заплатил за
- 21. Участок квадратной формы велосипедист объехал за 3
- 22. Подведём итоги!!!
- 23. III тур – 20 минутЗадача № 3.1.
- 24. Задача 3.1В квартирах №1, 2, 3 жили
- 25. Задача 3.2Когда ваши родители были детьми, молоко
- 26. Задача 3.3Фонтан на площади старинного города связан
- 27. ИГРА ЗАВЕРШЕНА! ПОДВЕДЕМ ИТОГИ
- 28. Спасибо за игру!
Слайд 3Да, путь познания не гладок.
Но знайте вы со школьных лет:
Загадок больше,
И поискам предела нет.
Величие человека –
в его способности мыслить.
Б. Паскаль
Слайд 4Регата - (итал. regata - от riga - ряд, линия)- спортивные
Математическая регата — соревнование школьных команд, составленных из учащихся одной параллели, в коллективном письменном решении математических задач.
Слайд 5Правила математической регаты
1. Математическая регата – командное соревнование по решению математических
2. Регата проводится в 4 тура: I тур – 5 задач, все последующие – по 3 задачи для коллективного письменного решения.
3. Решения задач оформляются и сдаются для проверки жюри. Каждое решение сдается на отдельном листе, причем команда имеет право сдать только по одному варианту решения каждой из задач.
4. Перед началом каждого тура командам сообщается время, отведенное для решения задач в данном туре, и стоимость задач в баллах.
5. Жюри проверяет предложенные командами решения и оценивает их в баллах, исходя из заявленной стоимости.
6. Жюри имеет право оштрафовать команду (снятием баллов, лишением права на участие в данном туре, дисквалификацией игрока или команды) за шум или некорректное поведение.
7. После каждого тура проводится разбор задач
8. Определение победителей и общее ранжирование команд производится исходя из общего количества набранных командами баллов.
Слайд 6I тур – разминка - 5 минут
Задача № 1.1.
Задача №1.2. --- 1 балл
Задача №1.3. --- 1 балл
Задача №1.4. --- 1 балл
Задача №1.5. --- 3 балла
Слайд 8 2. Трехзначное число состоит из возрастающих (слева направо) цифр. Если
Ответ: 147
Слайд 93.Ваня раскладывает на столе камешки на расстоянии 2 см один от
Решение:
промежутков между камешками 5,
2 камешка с краю и 4 – внутри.
Всего-6.
Ответ: 6 камешков.
Слайд 104. Какой цифрой заканчивается произведение всех нечётных чисел от 1 до
Ответ:
Решение:
произведение нечётных чисел при умножении на 5 дадут число с цифрой 5 на конце.
Слайд 13I тур – 10 минут
Задача № 1.1--- 3 балла
(длина линии)
Задача
(Стёпа и дедушка)
Задача № 1.3 --- 3 балла
(обезьяны и бананы)
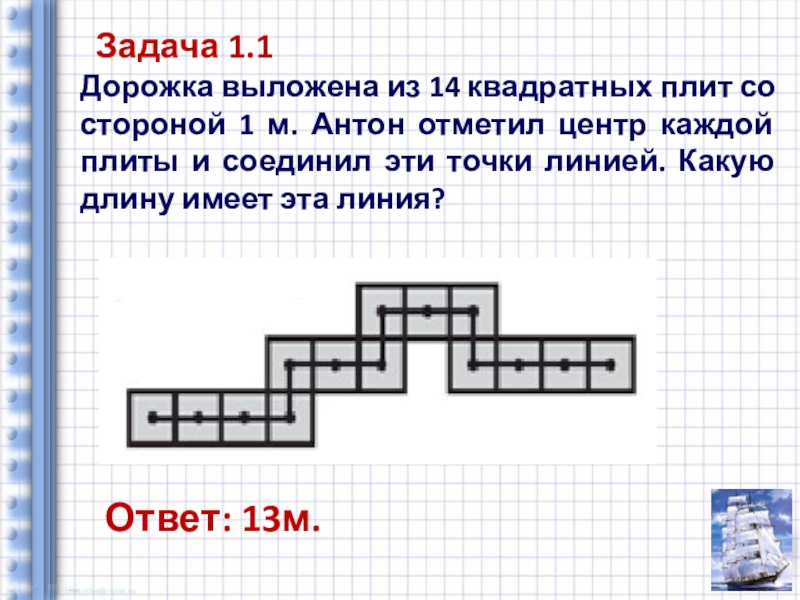
Слайд 14 Задача 1.1
Дорожка выложена из 14 квадратных плит со стороной
Ответ: 13м.
Слайд 15Задача 1.2
Степа учится в школе. Если цифры в его возрасте
Ответ: на 45 лет
определим, какие варианты возраста могут быть у Стёпы: 16, 26, 36, 46, 56, 66, 76, 86 или 96 лет. Однако так как Стёпа учится в школе, ему может быть только 16 лет. Следовательно, возраст его дедушки будет равен 61 году. В результате получаем, что Стёпа моложе дедушки на 61 - 16 = 45 лет.
Решение:
Слайд 16Нескольким обезьянам раздали 45 бананов так, что у каждой обезьяны получилось
обезьян могли получить бананы?
Задача 1.3
1+2+3+4+5+6+7+8+9=45
Решение:
Ответ: 9 обезьян
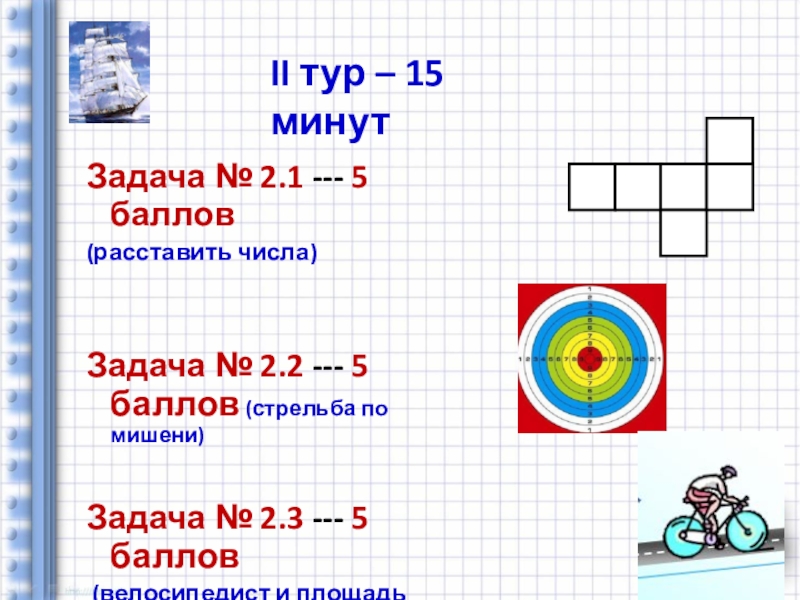
Слайд 18Задача № 2.1 --- 5 баллов
(расставить числа)
Задача № 2.2 ---
Задача № 2.3 --- 5 баллов
(велосипедист и площадь участка)
II тур – 15 минут
Слайд 19На рисунке изображена развертка кубика. На ней проставлены только числа 1
Задача 2.1
2
5
3
6
4
Ответ:
Слайд 20Ваня стреляет в тире. Он заплатил за 10 выстрелов. За каждое
Задача 2.2
20-10=10
10/2=5 попал по мешени
Решение:
Ответ: 5 раз
Слайд 21Участок квадратной формы велосипедист объехал за 3 часа со скоростью 12
Задача 2.3
Решение:
1) 3*12=36 (км)- расстояние, периметр.
2) 36:4=9 (км) -1 сторона
3) 9*9=81 (см2)
81 см2
Ответ:
Слайд 23III тур – 20 минут
Задача № 3.1. --- 7 баллов
(про
Задача № 3.2. --- 7 баллов (молоко и пустые бутылки)
Задача № 3.3. --- 7 баллов
(фонтан и часы)
Слайд 24Задача 3.1
В квартирах №1, 2, 3 жили три котенка: белый, черный
Черный котенок жил в квартире №3, белый – в квартире №2,
а рыжий – в квартире 1.
Решение и ответ:
Слайд 25Задача 3.2
Когда ваши родители были детьми, молоко продавали в литровых и
Решение:
Максимум принесёт 5 литров
молока в литровых бутылках.
Ответ:
Выгоднее сдавать бутылки по 0,5 л. За такие бутылки Петя выручит
15 ∙ 6=90 (коп.)
Если сдать все по 0,5 л и 1 литровую бутылки,
то можно получить
90+20=110 (коп.)
На эти деньги в пять оставшихся бутылок по 1 л можно купить 110:22=5 (л)
Слайд 26Задача 3.3
Фонтан на площади старинного города связан с часами на башне:
Решение:
В сутках 24 часа. Когда маленькая стрелка находится между 3 и 4 и 8 и 9 - проходит 4 часа (по два на утро и на вечер)
Остается двадцать часов. Каждый час проходит 10 минут когда большая стрелка попадает в эти отрезки - итого 200 минут или 3 часа 20 минут. В сумме 7 часов 20 минут.
Ответ: 7ч 20 мин.