- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад аннотация по математике по основным темам, изучаемым в 5 классе.
Содержание
- 1. Презентация-аннотация по математике по основным темам, изучаемым в 5 классе.
- 2. ОглавлениеНатуральные числаТреугольникиУравненияОбыкновенные дробиДесятичные числа
- 3. Что такое натуральные числа?Натуральными числами называют числа,
- 4. Какие числа не являются натуральными?Число ноль не
- 5. Какие существуют подходы к определению натуральных чисел?Существуют
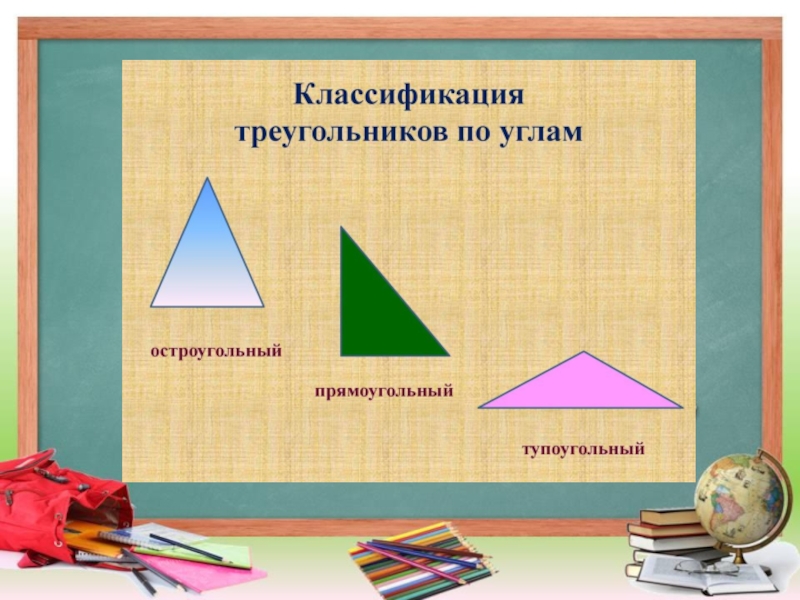
- 6. ТреугольникТреугольник- это геометрическая фигура,
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Медиана треугольника (m)— отрезок, соединяющий вершину треугольника
- 11. Уравнения
- 12. Уравнения
- 13. Уравнение - математическое равенство, содержащее одно или
- 14. Корень уравнения
- 15. Решить уравнение 36+Х=96X=96-36X=6036+60=9696=96- значит найти все его корни или доказать, что корней нет.
- 16. Обыкновенные дроби¼ ½
- 17. Обыкновенные дробиОбыкновенные дроби – это число, состоящееиз
- 18. ¼
- 19. Сколько лепестков у цветка?81 лепесток – 1
- 20. 3 88- знаменатель дроби числитель дроби - это дробь 3
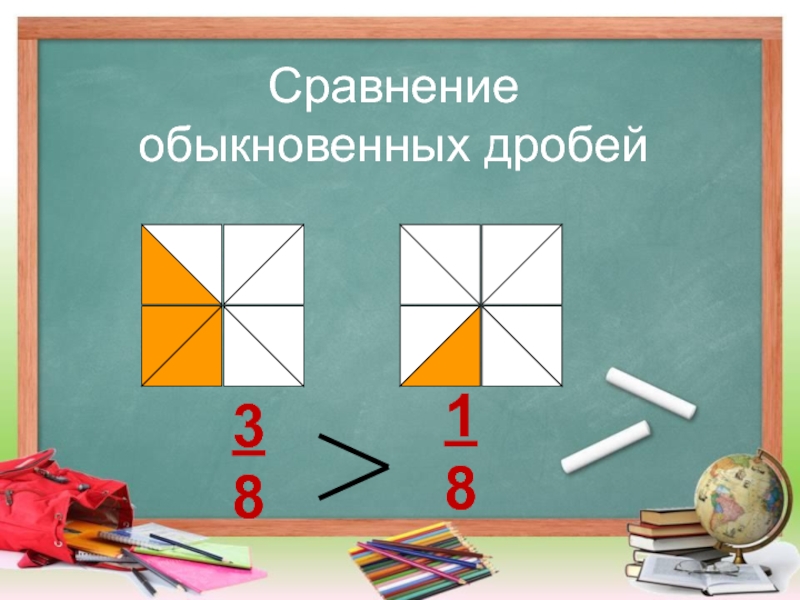
- 21. Сравнение обыкновенных дробей1838
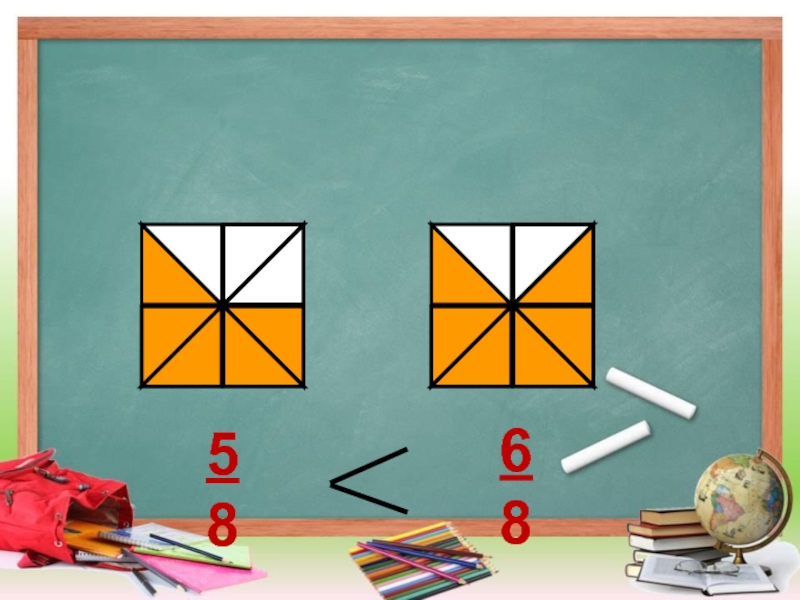
- 22. 6858
- 23. 4824=12=
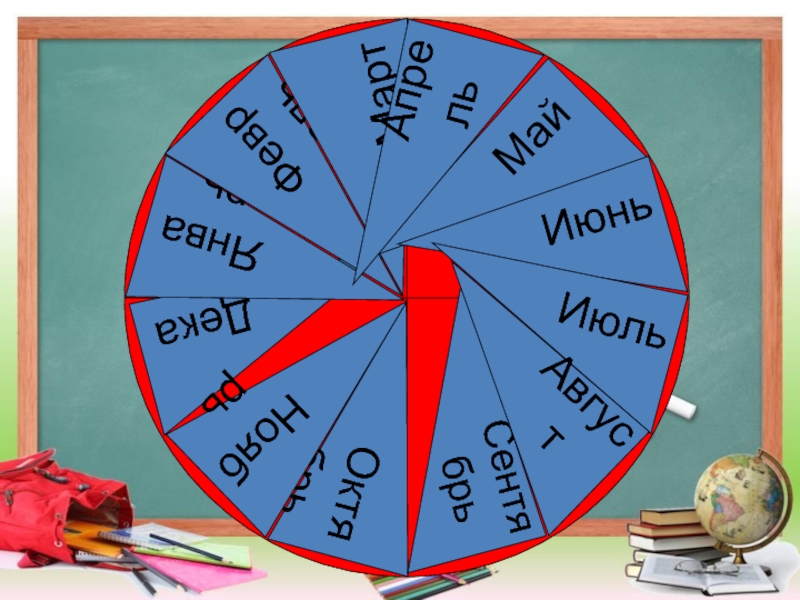
- 24. Декабрь Октябрь Январь Февраль МартСентябрьМайИюньИюльАпрельАвгуст Ноябрь
- 25. 1 месяц = года1 12
- 26. Десятичные дроби
- 27. Что такое десятичные дроби?Десятичная дробь-разновидность дроби, которая представляет собой способ представления действительных чисел.
- 28. Сначала пишем целую часть, а потом
- 29. Запомните!Если количество нулей превышает количество знаков (цифр)
- 30. Правила десятичной записи дробных чиселСначала пишут целую
- 31. Кто придумал десятичные дроби?Симон Стевин стал известен
- 32. Сложение десятичных дробейСложение десятичных дробей выполняется по
- 33. Запомните!Если исходные десятичные дроби имеют разное количество
ОглавлениеНатуральные числаТреугольникиУравненияОбыкновенные дробиДесятичные числа
Слайд 3Что такое натуральные числа?
Натуральными числами называют числа, которые используют при счете
или для указания порядкого номера среди однородных предметов.
Например:
2 37 147
Например:
2 37 147
Слайд 4Какие числа не являются натуральными?
Число ноль не является натуральным ,потому –что,
оно не используется в указание однородных предметов.
Слайд 5Какие существуют подходы к определению натуральных чисел?
Существуют два подхода к определению
натуральных чисел:
натуральные числа — числа, возникающие при подсчёте (нумерации) предметов (первый, второй, третий, четвёртый, пятый"…);
натуральные числа — числа, возникающие при обозначении количества предметов
(0 предметов, 1 предмет, 2 предмета,
3 предмета, 4 предмета, 5 предметов").
натуральные числа — числа, возникающие при подсчёте (нумерации) предметов (первый, второй, третий, четвёртый, пятый"…);
натуральные числа — числа, возникающие при обозначении количества предметов
(0 предметов, 1 предмет, 2 предмета,
3 предмета, 4 предмета, 5 предметов").
Слайд 6 Треугольник
Треугольник- это геометрическая фигура, образованная тремя отрезками. Три
точки, образующие треугольник, называются вершинами треугольника, а отрезки — сторонами треугольника.
Слайд 10Медиана треугольника (m)— отрезок,
соединяющий вершину треугольника
с серединой противоположной стороны.
Биссектриса
треугольника (b) — отрезок,
соединяющий вершину треугольника с точкой
противоположной стороны.
соединяющий вершину треугольника с точкой
противоположной стороны.
Слайд 13
Уравнение - математическое равенство, содержащее одно или несколько неизвестных величин и
сохраняющее свою силу только при определённых значениях этих неизвестных величин.
Слайд 15Решить уравнение
36+Х=96
X=96-36
X=60
36+60=96
96=96
- значит найти все его корни или доказать, что
корней нет.
Слайд 17Обыкновенные дроби
Обыкновенные дроби – это число, состоящее
из одной или нескольких частей
единицы (а), которые разделяют на несколько частей (b)
(половина, четверть, треть, одна сотая, полтора). Например: ½
(половина, четверть, треть, одна сотая, полтора). Например: ½
Слайд 19Сколько лепестков у цветка?
8
1 лепесток – 1 часть цветка.
3 лепестка -
? части
3 части
от 8 лепестков
3
8
3
Слайд 27Что такое десятичные дроби?
Десятичная дробь-разновидность дроби, которая представляет собой способ представления действительных
чисел.
Слайд 28 Сначала пишем целую часть, а потом ставим запятую и записываем
числитель дробной части.
КАК ЗАПИСЫВАЕТСЯ
ДЕСЯТИЧНАЯ ДРОБЬ?
Слайд 29Запомните!
Если количество нулей превышает
количество знаков (цифр) в числителе, то на
недостающие места ставим нули.
Слайд 30Правила десятичной записи дробных чисел
Сначала пишут целую часть,потом числитель дробной части.Целую
часть отделяют запятой.
Если дробь правильная,то перед запятой пишут цифру 0.
После запятой числитель дробной части должен иметь столько же цифр сколько нулей в знаменателе.
Если дробь правильная,то перед запятой пишут цифру 0.
После запятой числитель дробной части должен иметь столько же цифр сколько нулей в знаменателе.
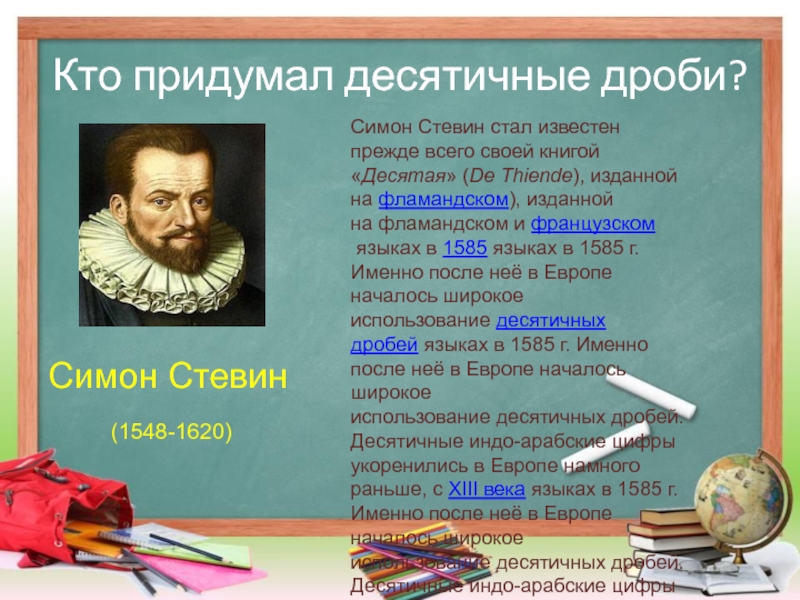
Слайд 31Кто придумал десятичные дроби?
Симон Стевин стал известен прежде всего своей книгой
«Десятая» (De Thiende), изданной на фламандском), изданной на фламандском и французском
языках в 1585 языках в 1585 г. Именно после неё в Европе началось широкое использование десятичных дробей языках в 1585 г. Именно после неё в Европе началось широкое использование десятичных дробей. Десятичные индо-арабские цифры укоренились в Европе намного раньше, с XIII века языках в 1585 г. Именно после неё в Европе началось широкое использование десятичных дробей. Десятичные индо-арабские цифры укоренились в Европе намного раньше, с XIII века, а вот дроби использовались либо натуральные языках в 1585 г. Именно после неё в Европе началось широкое использование десятичных дробей. Десятичные индо-арабские цифры укоренились в Европе намного раньше, с XIII века, а вот дроби использовались либо натуральные, либо шестидесятеричные, либо масштабированные до целых чисел.
языках в 1585 языках в 1585 г. Именно после неё в Европе началось широкое использование десятичных дробей языках в 1585 г. Именно после неё в Европе началось широкое использование десятичных дробей. Десятичные индо-арабские цифры укоренились в Европе намного раньше, с XIII века языках в 1585 г. Именно после неё в Европе началось широкое использование десятичных дробей. Десятичные индо-арабские цифры укоренились в Европе намного раньше, с XIII века, а вот дроби использовались либо натуральные языках в 1585 г. Именно после неё в Европе началось широкое использование десятичных дробей. Десятичные индо-арабские цифры укоренились в Европе намного раньше, с XIII века, а вот дроби использовались либо натуральные, либо шестидесятеричные, либо масштабированные до целых чисел.
Симон Стевин
(1548-1620)
Слайд 32Сложение десятичных дробей
Сложение десятичных дробей выполняется по правилам сложения в столбик.
При
сложении десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения. При этом запятые должны стоять чётко друг под другом.
Складывают десятичные дроби в столбик как натуральные числа, не обращая внимания на запятые.
В ответе запятую ставим под запятыми в исходных дробях.
Складывают десятичные дроби в столбик как натуральные числа, не обращая внимания на запятые.
В ответе запятую ставим под запятыми в исходных дробях.
Слайд 33Запомните!
Если исходные десятичные дроби имеют разное количество знаков (цифр) после запятой,
то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.