- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Подготовка к ГИА-2014. Решение задания C5. Геометрическая задача на доказательство
Содержание
- 1. Подготовка к ГИА-2014. Решение задания C5. Геометрическая задача на доказательство
- 2. № 1. В параллелограмме АВСD точки E,
- 3. №2. . В окружности с центром
- 4. № 3 Дан правильный восьмиугольник. Докажите, что
- 5. САМОСТОЯТЕЛЬНАЯ РАБОТА : В равностороннем треугольнике
- 6. ДОМАШНЕЕ ЗАДАНИЕ : Математика. Типовые тестовые задания 2014. И.В.Ященко, С.А.Шестаков.Вариант № 10
- 7. Спасибо за внимание !
Слайд 1Подготовка к ГИА-2014
Решение задания C5.
Геометрическая задача на доказательство
Разработка учителя математики
МБОУ ООШ № 9,Краснодарского края, Каневского района, х.Труд.
Коробка Марины Андреевны.
Слайд 2№ 1. В параллелограмме АВСD точки E, F, K и М
Доказательство :
Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, то треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма данный четырехугольник является параллелограммом.
Слайд 3 №2. . В окружности с центром О проведены две хорды
Доказательство :
Треугольники АОВ и СОD равны по двум сторонам и углу между ними (AO = BO = CO = DO как радиусы окружности, ∠AOB = ∠COD по условию).
Следовательно, высоты OK и OL равны как соответственные элементы равных треугольников.
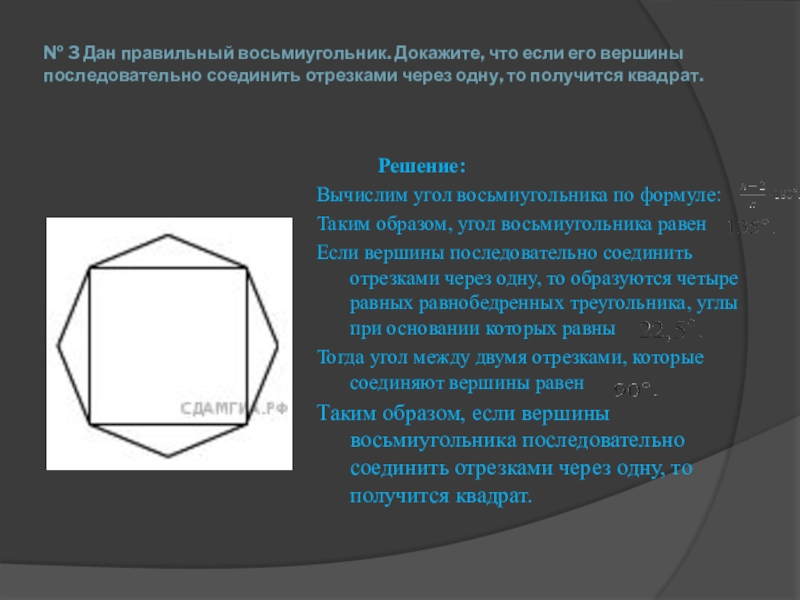
Слайд 4№ 3 Дан правильный восьмиугольник. Докажите, что если его вершины последовательно
Решение:
Вычислим угол восьмиугольника по формуле:
Таким образом, угол восьмиугольника равен
Если вершины последовательно соединить отрезками через одну, то образуются четыре равных равнобедренных треугольника, углы при основании которых равны
Тогда угол между двумя отрезками, которые соединяют вершины равен
Таким образом, если вершины восьмиугольника последовательно соединить отрезками через одну, то получится квадрат.
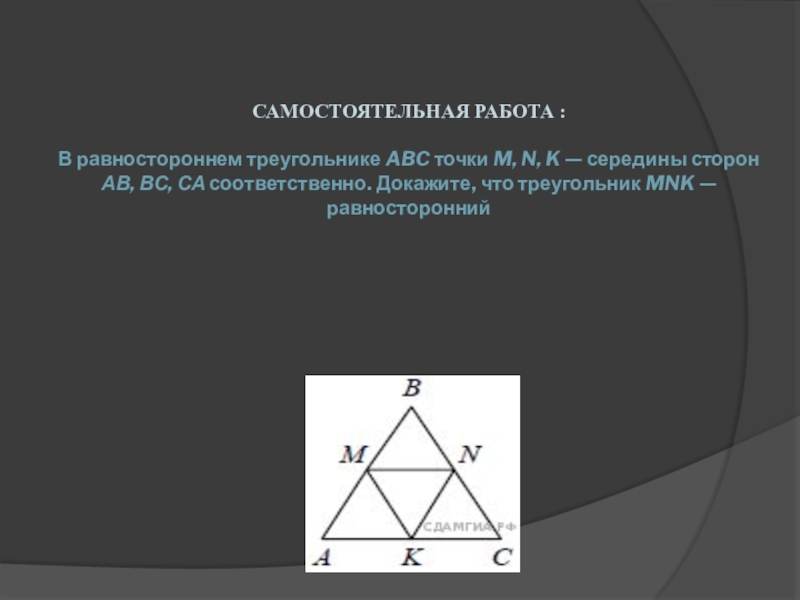
Слайд 5САМОСТОЯТЕЛЬНАЯ РАБОТА : В равностороннем треугольнике ABC точки M, N, K —